
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теорема о проекциях скоростей.
3.5. Теорема. Проекции векторов скоростей
Здесь
Доказательство: Рассмотрим движение двух произвольных точек Значение теоремы. 1. Теорема позволяет найти одну из входящих в (3.12) алгебраических величин по трем другим известным величинам. 2. Формула (3.12) допускает простую механическую интерпретацию движения плоской фигуры. Действительно,
Пример 3.2. Воспользовавшись условием примера 3.1, найти скорость точки Решение. Если бы задачу пришлось решать с самого начала, то пришлось бы вначале определить направления векторов скоростей Замечание. Пользуясь только теоремой о проекциях скоростей, угловую скорость шатуна
|
|||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 430; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.130.130 (0.008 с.) |
 и
и  двух точек
двух точек  и
и  твердого тела на ось, проходящую через эти точки, равны.
твердого тела на ось, проходящую через эти точки, равны. (3.12)
(3.12) - модули векторов скоростей соответствующих точек,
- модули векторов скоростей соответствующих точек,  - углы, которые образуют векторы
- углы, которые образуют векторы  с осью
с осью  . По теореме о проекциях скоростей можно определить одну из четырех величин, входящих в (3.12). Три другие величины должны быть известны.
. По теореме о проекциях скоростей можно определить одну из четырех величин, входящих в (3.12). Три другие величины должны быть известны.
 . Соответствующие построения показаны на рис. 3.8 и раньше на рис. 3.6. При этом можно пока предполагать, что векторы
. Соответствующие построения показаны на рис. 3.8 и раньше на рис. 3.6. При этом можно пока предполагать, что векторы  известны. Спроецируем равенство (3.7) на ось
известны. Спроецируем равенство (3.7) на ось  . Что и требовалось доказать.
. Что и требовалось доказать. ,
,  - это алгебраические величины скоростей двух точек фигуры в направлении оси
- это алгебраические величины скоростей двух точек фигуры в направлении оси  в направлении
в направлении  . «Насильственное» нарушение указанных требований в реальных механизмах приводит к разрушению механизма «заклиниванием».
. «Насильственное» нарушение указанных требований в реальных механизмах приводит к разрушению механизма «заклиниванием». , как это было сделано в примере 3.1. Далее пришлось бы мысленно провести ось, например, например,
, как это было сделано в примере 3.1. Далее пришлось бы мысленно провести ось, например, например,  , проходящую через точки
, проходящую через точки 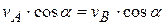 . Отсюда
. Отсюда  , что совпадает с результатом предыдущего примера.
, что совпадает с результатом предыдущего примера. определить не можем.
определить не можем.


