
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теорема о геометрическом сложении векторов ускорений.
3.11. Теорема.Вектор ускорения
Доказательство: По теореме о сложении векторов скоростей (3.7) вектор скорости произвольной точки плоской фигуры
Здесь Геометрическая интерпретация формулы (3.24) для одного из возможных вариантов движения фигуры представлена на рис. 3.17. В общем случае полюс А может двигаться по любой траектории – прямолинейной или криволинейной. Отрезок АВ вращается, поэтому траектория точки В – кривая линия. Следовательно, вектор
Величины векторов
Где
Здесь Вектор Направление вектора Если точка А, которую решено принять за полюс, движется по известной криволинейной траектории, то и вектор
И последнее, если и точка В движется по известной криволинейной траектории, то формулу (3.25) можно будет записать в самом общем виде:
Уравнения (3.24) - (3.29) позволяют вычислить вектор ускорения произвольной точки
2. Метод проекций для определения ускорений С методом проекций мы уже сталкивались при обсуждении методов определения скоростей. С математической стороны здесь все делается так же, но применительно к другим механическим уравнениям. Введем на плоскости некоторую прямоугольную систему координат
Все входящие в эти уравнения величины – это проекции соответствующих векторов. Из системы уравнений (3.30) могут быть определены любые две входящие в них величины. Остальные величины должны быть известны заранее. Если, например, из системы (3.30) определены проекции вектора ускорения точки В -
Направление вектора Пример 3.11. Стержень
Решение. Стержень в данный момент времени вращается замедленно, так как
где
|
||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 569; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.217.144.32 (0.007 с.) |
 произвольной точки В плоской фигуры в плоско - параллельном движении равен геометрической сумме вектора ускорения
произвольной точки В плоской фигуры в плоско - параллельном движении равен геометрической сумме вектора ускорения  точки А, принятой за полюс, и вектора ускорения
точки А, принятой за полюс, и вектора ускорения  , которое точка В приобретает при вращении плоской фигуры относительно полюса А (рис.3.19):
, которое точка В приобретает при вращении плоской фигуры относительно полюса А (рис.3.19): (3.24)
(3.24) . Продифференцируем последнее равенство по времени и получим:
. Продифференцируем последнее равенство по времени и получим: =
=  +
+  .
. - вектор ускорения полюса А.
- вектор ускорения полюса А.  - вектор ускорения точки В, которое оно приобретает от вращения фигуры (другими словами, отрезка АВ) относительно полюса А. Окончательно, вектор ускорения точки В вычисляется по формуле
- вектор ускорения точки В, которое оно приобретает от вращения фигуры (другими словами, отрезка АВ) относительно полюса А. Окончательно, вектор ускорения точки В вычисляется по формуле  . Что и требовалось доказать.
. Что и требовалось доказать. , что бывает удобно в практических расчетах (рис.3.18, рис.3.19). При этом (3.24) принимает вид:
, что бывает удобно в практических расчетах (рис.3.18, рис.3.19). При этом (3.24) принимает вид: +
+  (3.25)
(3.25) вычисляются по формулам теории вращательного движения относительно неподвижной оси:
вычисляются по формулам теории вращательного движения относительно неподвижной оси: ,
,  , (3.26)
, (3.26)
 - угловая скорость и угловое ускорение плоской фигуры соответственно. С учетом (3.26) имеем:
- угловая скорость и угловое ускорение плоской фигуры соответственно. С учетом (3.26) имеем: . (3.27)
. (3.27)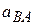 и m – модуль и угол отклонения вектора
и m – модуль и угол отклонения вектора 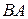 соответственно.
соответственно. , независимо от направления вращения фигуры (рис. 3.18, рис. 3.19), направлен от точки В к мгновенной оси вращения, проходящей через точку А. Другими словами, вектор
, независимо от направления вращения фигуры (рис. 3.18, рис. 3.19), направлен от точки В к мгновенной оси вращения, проходящей через точку А. Другими словами, вектор 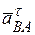 (рис. 3.18, рис. 3.19) соответствует направлению дуговой стрелки углового ускорения
(рис. 3.18, рис. 3.19) соответствует направлению дуговой стрелки углового ускорения  и не зависит от направления вращения фигуры, то есть не зависит от направления дуговой стрелки
и не зависит от направления вращения фигуры, то есть не зависит от направления дуговой стрелки 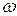 .
. , а формула (3.25) примет вид:
, а формула (3.25) примет вид: (3.28)
(3.28)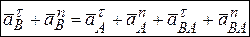 (3.29)
(3.29) В плоской фигуры. При этом предполагается, что все другие векторы, входящие в эти уравнения, или известны заранее, или могут быть вычислены по исходным данным задачи. Но совершенно очевидно, что эти уравнения справедливы и для случая, когда вектор
В плоской фигуры. При этом предполагается, что все другие векторы, входящие в эти уравнения, или известны заранее, или могут быть вычислены по исходным данным задачи. Но совершенно очевидно, что эти уравнения справедливы и для случая, когда вектор  известен. В этом случае они позволяют найти любой другой один вектор по известным остальным векторам (из одного уравнения можно найти одно неизвестное).
известен. В этом случае они позволяют найти любой другой один вектор по известным остальным векторам (из одного уравнения можно найти одно неизвестное).  . Начало координат О, и направление осей выбираются произвольно. Спроецировав любое из уравнений (3.24)-(3.29) на эти оси, получают соответствующие уравнения метода проекций. Например, векторное уравнение (3.29) заменится двумя скалярными уравнениями:
. Начало координат О, и направление осей выбираются произвольно. Спроецировав любое из уравнений (3.24)-(3.29) на эти оси, получают соответствующие уравнения метода проекций. Например, векторное уравнение (3.29) заменится двумя скалярными уравнениями: ,
,  . (3.30)
. (3.30) , то модуль вектора ускорения
, то модуль вектора ускорения  находится по формуле:
находится по формуле: . (3.31)
. (3.31) . Выбор осей координат не влияет на конечный результат, но может существенно облегчить или затруднить вычисления
. Выбор осей координат не влияет на конечный результат, но может существенно облегчить или затруднить вычисления движется в плоскости. В данный момент времени точки
движется в плоскости. В данный момент времени точки  имеет ускорение
имеет ускорение  , угловое ускорение
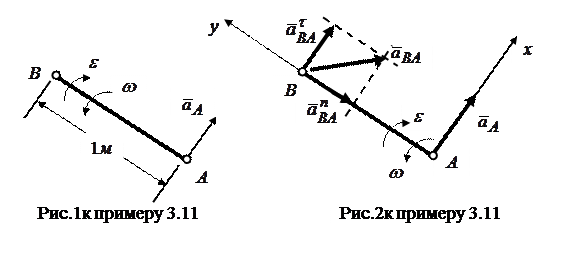
, угловое ускорение  . Направление угловой скорости и углового ускорения показаны дуговыми стрелками на рисунке 1 к примеру. Определить величину ускорения точки
. Направление угловой скорости и углового ускорения показаны дуговыми стрелками на рисунке 1 к примеру. Определить величину ускорения точки  стержня, если длина его
стержня, если длина его  , а модуль вектора ускорения
, а модуль вектора ускорения  .
.
 ,
,  .
.  ,
,  , (*)
, (*) ,
,  =
=  ,
,  ,
,  ,
, 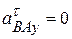 ,
, 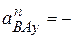
 . Удачный выбор осей координат существенно облегчил нахождение проекций, многие из них равны нулю. Окончательно из (*) получим
. Удачный выбор осей координат существенно облегчил нахождение проекций, многие из них равны нулю. Окончательно из (*) получим  ,
,  ,
,  Ответ:
Ответ: 



