
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Мгновенный центр ускорений (МЦУ). Определение ускорений точки плоской фигуры с использованием мгновенного центра ускорений
3.12. Мгновенным центром ускорений Слово «мгновенный» указывает на то, что при плоскопараллельном движении плоской фигуры положение этой точки в общем случае меняется с течением времени и может быть определено для конкретного момента времени. Так же было и с мгновенным центром скоростей. Пусть положение МЦУ известно. Примем её за полюс. Тогда ускорение произвольной точки Величины векторов
Здесь
m – угол отклонения вектора Как определить мгновенный центр ускорений (МЦУ)? Рассмотрим два частных случая. Первый случай. Известен вектор ускорения 1. Изобразить вектор Докажем, что
Второй случай. Пусть известны только направления векторов ускорений
1. Вычислить угол Сравнивая ускорения разных точек плоской фигуры, вычисленные по (3.33), находим, что они пропорциональны их расстояниям от мгновенного центра ускорений.
3.13. Если мгновенный центр ускорений 1. Находится расстояние
|
|||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 568; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.24.202 (0.03 с.) |
 плоской фигуры называется точка в плоскости движения фигуры, ускорение которой равно нулю (
плоской фигуры называется точка в плоскости движения фигуры, ускорение которой равно нулю (  ).
). плоской фигуры вычисляется по формулам (3.24) и (3.25), которые теперь принимают вид:
плоской фигуры вычисляется по формулам (3.24) и (3.25), которые теперь принимают вид:  Отсюда
Отсюда  так как
так как  любой точки
любой точки  этой точки во вращательном движении плоской фигуры относительно МЦУ (
этой точки во вращательном движении плоской фигуры относительно МЦУ ( ).
). вычисляются по формулам (3.26).
вычисляются по формулам (3.26). ,
, 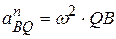 . (3.32)
. (3.32) - угловая скорость и угловое ускорение плоской фигуры соответственно,
- угловая скорость и угловое ускорение плоской фигуры соответственно,  - расстояние от мгновенного центра ускорений
- расстояние от мгновенного центра ускорений  . (3.33)
. (3.33) (3.34)
(3.34) соответственно.
соответственно.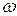 и угловое ускорение
и угловое ускорение  самой фигуры. Для определения
самой фигуры. Для определения  по формуле (3.33). 3. Мысленно повернуть вектор
по формуле (3.33). 3. Мысленно повернуть вектор  . 4. Вычислить длину отрезка
. 4. Вычислить длину отрезка 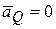 . Выберем точку
. Выберем точку  точки
точки  , где
, где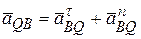 . Модуль вектора
. Модуль вектора 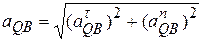 = =
= = 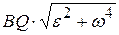 . Но по построению
. Но по построению  =
= 
 . Далее, прямая
. Далее, прямая  отклонена от вектора
отклонена от вектора  отклонен от направления
отклонен от направления  , что показано на рис.3.20. Тогда
, что показано на рис.3.20. Тогда 
 . Что и требовалось доказать.
. Что и требовалось доказать.
 двух точек
двух точек  плоской фигуры (модули не известны), угловая скорость
плоской фигуры (модули не известны), угловая скорость  и
и  и
и  . 3. Точка пересечения этих лучей определит положение мгновенного центра ускорений
. 3. Точка пересечения этих лучей определит положение мгновенного центра ускорений  (3.35)
(3.35) точки
точки  от точки
от точки  ) (рис. 3.20).
) (рис. 3.20).


