1) Качение катка по плоскости без скольжения (без проскальзывания или, еще говорят, без «буксовки»).
Мгновенный центр скоростей находится в точке  , где каток касается плоскости. Действительно, точки плоскости не подвижны. Каток катится без скольжения. Следовательно, в точке касания скорости тел (катка и плоскости) должны быть одинаковыми и равными нулю. Если известна скорость точки
, где каток касается плоскости. Действительно, точки плоскости не подвижны. Каток катится без скольжения. Следовательно, в точке касания скорости тел (катка и плоскости) должны быть одинаковыми и равными нулю. Если известна скорость точки  , то угловая скорость катка вычисляется по формуле:
, то угловая скорость катка вычисляется по формуле:
 , где
, где 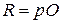 - радиус катка.
- радиус катка.  . Оказывается, что мгновенная скорость песчинки, прилипшей к колесу автомобиля в точке
. Оказывается, что мгновенная скорость песчинки, прилипшей к колесу автомобиля в точке  , в два раза больше скорости точки оси
, в два раза больше скорости точки оси  , которую мы видим на спидометре своего автомобиля. Вектор скорости точки
, которую мы видим на спидометре своего автомобиля. Вектор скорости точки  , лежащей на конце горизонтального диаметра, направлен к точке
, лежащей на конце горизонтального диаметра, направлен к точке  , так как известно, что угол, вписанный в окружность и опирающийся на диаметр, - прямой. Тогда,
, так как известно, что угол, вписанный в окружность и опирающийся на диаметр, - прямой. Тогда,  .
.














































2) Векторы скоростей двух точек плоской фигуры  и
и  параллельны, направлены в одну сторону, но точки не лежат на общем перпендикуляре, восстановленном к одному из векторов скоростей (рис. 3.15). Мгновенный центр скоростей находится в бесконечности и угловая скорость фигуры
параллельны, направлены в одну сторону, но точки не лежат на общем перпендикуляре, восстановленном к одному из векторов скоростей (рис. 3.15). Мгновенный центр скоростей находится в бесконечности и угловая скорость фигуры 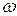 равна нулю.
равна нулю.
 (3.16)
(3.16)

Действительно, по (3.14)  ,
,  . При этом
. При этом 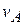 и
и  - конечные величины. Параллельные прямые
- конечные величины. Параллельные прямые 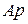 и
и  пересекаются в бесконечности. Тогда по (3.15),
пересекаются в бесконечности. Тогда по (3.15), 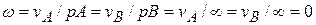 (МЦС не существует). Это означает, что тело в данный момент времени совершает мгновенно поступательное движение, векторы скоростей всех точек тела параллельны и равны по модулю.
(МЦС не существует). Это означает, что тело в данный момент времени совершает мгновенно поступательное движение, векторы скоростей всех точек тела параллельны и равны по модулю.
 Пример 3.7. Кривошипно-шатунный механизм
Пример 3.7. Кривошипно-шатунный механизм  приводится в движение вращением кривошипа
приводится в движение вращением кривошипа  с угловой скоростью
с угловой скоростью  . Точка
. Точка  одновременно принадлежит шатуну
одновременно принадлежит шатуну  и кривошипу
и кривошипу  . Кривошип
. Кривошип  вращается относительно неподвижной оси
вращается относительно неподвижной оси  (на рис. не показана), проходящей через точку
(на рис. не показана), проходящей через точку  , перпендикулярно плоскости рисунка. Следовательно, вектор скорости
, перпендикулярно плоскости рисунка. Следовательно, вектор скорости  точки
точки  направлен перпендикулярно к оси кривошипа
направлен перпендикулярно к оси кривошипа  в сторону вращения кривошипа. Вектор
в сторону вращения кривошипа. Вектор  в данный момент времени параллелен оси
в данный момент времени параллелен оси  . По величине он равен
. По величине он равен  .
.
В точке  в механизме - ползун, который позволяет точке
в механизме - ползун, который позволяет точке  двигаться только вдоль своей оси
двигаться только вдоль своей оси  . Следовательно, вектор скорости точки
. Следовательно, вектор скорости точки  параллелен вектору
параллелен вектору  и оба вектора направлены в одну сторону. МЦС шатуна находится в бесконечности. Следовательно, шатун движется мгновенно поступательно и все его точки движутся с одинаковыми по величине и направлению скоростями. Замечание. Сравните этот пример с примером 3.6 и убедитесь в том, что в другие моменты времени шатун вращается.
и оба вектора направлены в одну сторону. МЦС шатуна находится в бесконечности. Следовательно, шатун движется мгновенно поступательно и все его точки движутся с одинаковыми по величине и направлению скоростями. Замечание. Сравните этот пример с примером 3.6 и убедитесь в том, что в другие моменты времени шатун вращается.

Пример 3.8. В эпициклическом механизме кривошип  длиной
длиной  вращается с угловой скоростью
вращается с угловой скоростью  и приводит в движение колесо
и приводит в движение колесо  радиусом
радиусом  . Колесо
. Колесо  находится во внешнем зацеплении без проскальзывания с колесом
находится во внешнем зацеплении без проскальзывания с колесом  , вращающимся с угловой скоростью
, вращающимся с угловой скоростью  . Колесо
. Колесо  и ползун
и ползун  соединены шарнирно шатуном
соединены шарнирно шатуном  . Определить скорости точек
. Определить скорости точек  механизма и угловую скорость
механизма и угловую скорость  колеса
колеса  , угловую скорость
, угловую скорость  шатуна
шатуна  .
.
Решение.  . Так как в точке касания
. Так как в точке касания  колеса
колеса  и
и  не проскальзывают относительно друг друга, то линейные скорости точек
не проскальзывают относительно друг друга, то линейные скорости точек 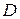 и первого, и второго колес равны.
и первого, и второго колес равны.  . Вектор линейной скорости точки
. Вектор линейной скорости точки 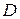 найдем по известному вращению колеса
найдем по известному вращению колеса  . По величине
. По величине  . Вектор
. Вектор  направлен в сторону вращения колеса
направлен в сторону вращения колеса  и перпендикулярен радиусу
и перпендикулярен радиусу  второго колеса, который в данный момент времени совпадает по направлению с кривошипом
второго колеса, который в данный момент времени совпадает по направлению с кривошипом  . Скорости двух точек одного и того же тела (колеса 1) оказались равными и по величине, и по направлению. Следовательно, колесо 1 совершает мгновенно поступательное движение, то есть не вращается и
. Скорости двух точек одного и того же тела (колеса 1) оказались равными и по величине, и по направлению. Следовательно, колесо 1 совершает мгновенно поступательное движение, то есть не вращается и  . Шатун
. Шатун  в данном его положении движется поступательно и
в данном его положении движется поступательно и  . Это было показано в предыдущем примере. Окончательно, векторы скоростей всех точек
. Это было показано в предыдущем примере. Окончательно, векторы скоростей всех точек  параллельны и равны по величине
параллельны и равны по величине  .
.

3) Векторы скоростей  и
и  двух точек плоской фигуры параллельны, не равны друг другу по модулю, а сами точки лежат на общем перпендикуляре к векторам скоростей (рис. 3.16). МЦС (точка р) находится на пересечении прямой АВ и прямой, проходящей через концы векторов скоростей.
двух точек плоской фигуры параллельны, не равны друг другу по модулю, а сами точки лежат на общем перпендикуляре к векторам скоростей (рис. 3.16). МЦС (точка р) находится на пересечении прямой АВ и прямой, проходящей через концы векторов скоростей.
При этом угловая скорость плоской фигуры вычисляется по формуле:
 (3.17)
(3.17)
Доказательство основано на применении соотношения (3.15).
Пример 3.9. Третий частный случай иллюстрируется движением механизма, положение которого в некоторый момент времени  показано на рис. к примеру. Механизм состоит из двух колес 1 и 2, плотно прижатых друг к другу (это могут быть и зубчатые колеса) и кривошипа
показано на рис. к примеру. Механизм состоит из двух колес 1 и 2, плотно прижатых друг к другу (это могут быть и зубчатые колеса) и кривошипа  , вращающегося относительно точки
, вращающегося относительно точки  и шарнирно (подшипник) соединенного с колесом 2 в точке
и шарнирно (подшипник) соединенного с колесом 2 в точке  . Кривошип
. Кривошип  и колесо 1 «сидят» на одной оси, но друг с другом не соединяются. Механизм приводится в движение независимыми вращениями колеса 1 и кривошипа
и колесо 1 «сидят» на одной оси, но друг с другом не соединяются. Механизм приводится в движение независимыми вращениями колеса 1 и кривошипа  . В данный момент времени угловые скорости их равны
. В данный момент времени угловые скорости их равны  и
и  соответственно и направлены так, как показано на рисунке к примеру 3.5. Таким образом, колесо
соответственно и направлены так, как показано на рисунке к примеру 3.5. Таким образом, колесо  и кривошип
и кривошип  совершают при работе механизма вращательное движение относительно неподвижной оси, а колесо
совершают при работе механизма вращательное движение относительно неподвижной оси, а колесо  совершает плоскопараллельное движение. Так как кривошип совершает вращательное движение относительно неподвижной оси, проходящей через точку
совершает плоскопараллельное движение. Так как кривошип совершает вращательное движение относительно неподвижной оси, проходящей через точку  перпендикулярно к плоскости рисунка (на рис. ось не показана), то вектор линейной скорости
перпендикулярно к плоскости рисунка (на рис. ось не показана), то вектор линейной скорости  точки
точки  кривошипа
кривошипа  и точки
и точки  колеса 2 перпендикулярен к оси кривошипа
колеса 2 перпендикулярен к оси кривошипа  и направлен в сторону его вращения (по криволинейной стрелке
и направлен в сторону его вращения (по криволинейной стрелке  ). Векторы линейной скорости
). Векторы линейной скорости  в точке касания колес
в точке касания колес  совпадают. Рассматривая вращение колеса 1 видим, что
совпадают. Рассматривая вращение колеса 1 видим, что  направлен перпендикулярно к радиусу вращающегося колеса 1 в сторону его вращения. Следовательно,
направлен перпендикулярно к радиусу вращающегося колеса 1 в сторону его вращения. Следовательно,  II
II  . Пусть при этом
. Пусть при этом  , как показано на рисунке. Тогда мгновенный центр скоростей колеса 2 оказывается в точке
, как показано на рисунке. Тогда мгновенный центр скоростей колеса 2 оказывается в точке  . Колесо 2 совершает мгновенное вращение относительно точки
. Колесо 2 совершает мгновенное вращение относительно точки  с мгновенной угловой скоростью
с мгновенной угловой скоростью  . При этом по формулам (3.14)
. При этом по формулам (3.14) 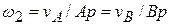 . Отсюда
. Отсюда  , где
, где  . Решая совместно два последних уравнения, получим:
. Решая совместно два последних уравнения, получим:
 . (3.18)
. (3.18)
Угловая скорость второго колеса по (3.15) будет равна:
 (3.19)
(3.19)
Направление  совпадает с направлениями
совпадает с направлениями  и
и  , что показано на рисунке. Это означает, что второе колесо «катится» без скольжения по первому, обегая его по часовой стрелке, так как при вращательных движениях тел направление векторов линейных скоростей точек тела и угловая скорость вращения самого тела всегда согласованы и «направлены в одну сторону».
, что показано на рисунке. Это означает, что второе колесо «катится» без скольжения по первому, обегая его по часовой стрелке, так как при вращательных движениях тел направление векторов линейных скоростей точек тела и угловая скорость вращения самого тела всегда согласованы и «направлены в одну сторону».
Пусть теперь модули векторов скоростей таковы, что  . Это может быть, если
. Это может быть, если  и
и 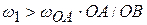 . Тогда мгновенный центр скоростей
. Тогда мгновенный центр скоростей  будет в точке, показанной на рис.2 к примеру 3.9. По аналогии с предыдущим случаем получим:
будет в точке, показанной на рис.2 к примеру 3.9. По аналогии с предыдущим случаем получим:
 , (3.20)
, (3.20)
 . (3.21)
. (3.21)
Как и раньше, направление угловой скорости  определяется по направлению векторов линейных скоростей
определяется по направлению векторов линейных скоростей  .
.


4) Векторы скоростей  и
и  двух точек плоской фигуры параллельны, не равны по модулю и направлены в разные стороны. Точки лежат на общем перпендикуляре АВ к векторам скоростей (рис. 3.17). МЦС (точка р) находится на пересечении прямой АВ и прямой, проходящей через концы векторов скоростей.
двух точек плоской фигуры параллельны, не равны по модулю и направлены в разные стороны. Точки лежат на общем перпендикуляре АВ к векторам скоростей (рис. 3.17). МЦС (точка р) находится на пересечении прямой АВ и прямой, проходящей через концы векторов скоростей.
При этом угловая скорость плоской фигуры вычисляется по формуле:
 (3.22)
(3.22)
Доказательство основано на применении соотношения (3.15).
Пример 3.10. Две параллельные рейки движутся в разные стороны с постоянными скоростями  . Между рейками зажат диск радиуса
. Между рейками зажат диск радиуса  , катящийся по рейкам без скольжения. Найти угловую скорость диска
, катящийся по рейкам без скольжения. Найти угловую скорость диска 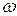 и числовое значение скорости
и числовое значение скорости  его центра
его центра  , если
, если  .
.

Решение: Так как диск катится без скольжения, то в точках касания  и
и  диска с рейками соответствующие скорости равны. А именно,
диска с рейками соответствующие скорости равны. А именно,  ,
,  . Так как рейки параллельны, то параллельны и вектора скоростей
. Так как рейки параллельны, то параллельны и вектора скоростей  и
и  точек
точек  и
и  диска, а сами точки лежат на общем перпендикуляре к векторам скоростей этих точек. Следовательно, мгновенный центр скоростей лежит на вертикальном диаметре диска между точками
диска, а сами точки лежат на общем перпендикуляре к векторам скоростей этих точек. Следовательно, мгновенный центр скоростей лежит на вертикальном диаметре диска между точками  и
и  , как показано на рис. 2 к примеру 3.10. Из пропорциональности точек плоской фигуры их расстояниям до мгновенного центра скоростей (3.16) имеем:
, как показано на рис. 2 к примеру 3.10. Из пропорциональности точек плоской фигуры их расстояниям до мгновенного центра скоростей (3.16) имеем:
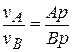 и
и 
Решая совместно последние два уравнения, находим расстояние  от точки
от точки  до мгновенного центра скоростей
до мгновенного центра скоростей  :
:  . Угловая скорость диска при его вращении относительно мгновенного центра скоростей
. Угловая скорость диска при его вращении относительно мгновенного центра скоростей  вычисляется по (3.15):
вычисляется по (3.15):  . Или
. Или
 (3.23)
(3.23)
Учитывая, что  , видим совпадение (3.23) и (3.22).
, видим совпадение (3.23) и (3.22).
Чтобы определить величину линейной скорости центра диска, вычислим расстояние  .
.
 .
.
Так как точка 
 - мгновенный центр скоростей диска, величина скорости центра диска
- мгновенный центр скоростей диска, величина скорости центра диска  вычисляется по формуле (3.15).
вычисляется по формуле (3.15).


 =
=  =
= 
Направление вектора  определяется по направлению вращения диска, то есть по направлению
определяется по направлению вращения диска, то есть по направлению 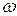 , и показано на рис.2 к примеру 3.10.
, и показано на рис.2 к примеру 3.10.















































 , где каток касается плоскости. Действительно, точки плоскости не подвижны. Каток катится без скольжения. Следовательно, в точке касания скорости тел (катка и плоскости) должны быть одинаковыми и равными нулю. Если известна скорость точки
, где каток касается плоскости. Действительно, точки плоскости не подвижны. Каток катится без скольжения. Следовательно, в точке касания скорости тел (катка и плоскости) должны быть одинаковыми и равными нулю. Если известна скорость точки  , то угловая скорость катка вычисляется по формуле:
, то угловая скорость катка вычисляется по формуле: , где
, где 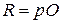 - радиус катка.
- радиус катка.  . Оказывается, что мгновенная скорость песчинки, прилипшей к колесу автомобиля в точке
. Оказывается, что мгновенная скорость песчинки, прилипшей к колесу автомобиля в точке  , в два раза больше скорости точки оси
, в два раза больше скорости точки оси  , лежащей на конце горизонтального диаметра, направлен к точке
, лежащей на конце горизонтального диаметра, направлен к точке  .
.

 и
и  параллельны, направлены в одну сторону, но точки не лежат на общем перпендикуляре, восстановленном к одному из векторов скоростей (рис. 3.15). Мгновенный центр скоростей находится в бесконечности и угловая скорость фигуры
параллельны, направлены в одну сторону, но точки не лежат на общем перпендикуляре, восстановленном к одному из векторов скоростей (рис. 3.15). Мгновенный центр скоростей находится в бесконечности и угловая скорость фигуры 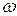 равна нулю.
равна нулю. (3.16)
(3.16)
 ,
,  . При этом
. При этом 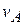 и
и  - конечные величины. Параллельные прямые
- конечные величины. Параллельные прямые 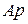 и
и  пересекаются в бесконечности. Тогда по (3.15),
пересекаются в бесконечности. Тогда по (3.15), 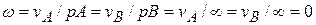 (МЦС не существует). Это означает, что тело в данный момент времени совершает мгновенно поступательное движение, векторы скоростей всех точек тела параллельны и равны по модулю.
(МЦС не существует). Это означает, что тело в данный момент времени совершает мгновенно поступательное движение, векторы скоростей всех точек тела параллельны и равны по модулю. Пример 3.7. Кривошипно-шатунный механизм
Пример 3.7. Кривошипно-шатунный механизм  приводится в движение вращением кривошипа
приводится в движение вращением кривошипа  с угловой скоростью
с угловой скоростью  . Точка
. Точка 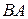 и кривошипу
и кривошипу  (на рис. не показана), проходящей через точку
(на рис. не показана), проходящей через точку  . По величине он равен
. По величине он равен  .
.
 вращается с угловой скоростью
вращается с угловой скоростью  и приводит в движение колесо
и приводит в движение колесо  радиусом
радиусом  . Колесо
. Колесо  , вращающимся с угловой скоростью
, вращающимся с угловой скоростью  . Колесо
. Колесо 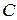 соединены шарнирно шатуном
соединены шарнирно шатуном  . Определить скорости точек
. Определить скорости точек  механизма и угловую скорость
механизма и угловую скорость  колеса
колеса  шатуна
шатуна  . Так как в точке касания
. Так как в точке касания 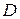 колеса
колеса  . Вектор линейной скорости точки
. Вектор линейной скорости точки  . Вектор
. Вектор  направлен в сторону вращения колеса
направлен в сторону вращения колеса  второго колеса, который в данный момент времени совпадает по направлению с кривошипом
второго колеса, который в данный момент времени совпадает по направлению с кривошипом  . Шатун
. Шатун  . Это было показано в предыдущем примере. Окончательно, векторы скоростей всех точек
. Это было показано в предыдущем примере. Окончательно, векторы скоростей всех точек  .
.
 (3.17)
(3.17) показано на рис. к примеру. Механизм состоит из двух колес 1 и 2, плотно прижатых друг к другу (это могут быть и зубчатые колеса) и кривошипа
показано на рис. к примеру. Механизм состоит из двух колес 1 и 2, плотно прижатых друг к другу (это могут быть и зубчатые колеса) и кривошипа  , как показано на рисунке. Тогда мгновенный центр скоростей колеса 2 оказывается в точке
, как показано на рисунке. Тогда мгновенный центр скоростей колеса 2 оказывается в точке  . При этом по формулам (3.14)
. При этом по формулам (3.14) 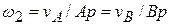 . Отсюда
. Отсюда  , где
, где  . Решая совместно два последних уравнения, получим:
. Решая совместно два последних уравнения, получим: . (3.18)
. (3.18) (3.19)
(3.19) . Это может быть, если
. Это может быть, если  и
и 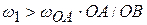 . Тогда мгновенный центр скоростей
. Тогда мгновенный центр скоростей  , (3.20)
, (3.20) . (3.21)
. (3.21) .
.

 (3.22)
(3.22) . Между рейками зажат диск радиуса
. Между рейками зажат диск радиуса  , катящийся по рейкам без скольжения. Найти угловую скорость диска
, катящийся по рейкам без скольжения. Найти угловую скорость диска  его центра
его центра  .
.
 ,
,  . Так как рейки параллельны, то параллельны и вектора скоростей
. Так как рейки параллельны, то параллельны и вектора скоростей 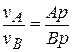 и
и 
 . Угловая скорость диска при его вращении относительно мгновенного центра скоростей
. Угловая скорость диска при его вращении относительно мгновенного центра скоростей  . Или
. Или (3.23)
(3.23) , видим совпадение (3.23) и (3.22).
, видим совпадение (3.23) и (3.22). .
. .
.
 вычисляется по формуле (3.15).
вычисляется по формуле (3.15).

 =
=  =
= 
 определяется по направлению вращения диска, то есть по направлению
определяется по направлению вращения диска, то есть по направлению 


