
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Глава 3. Плоскопараллельное движение твердого телаСодержание книги
Поиск на нашем сайте
ГЛАВА 3. ПЛОСКОПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
§ 3.1. Общие понятия и определения 3.1. Плоскопараллельным или плоским называется такое движение твердого тела, при котором каждая его точка движется в плоскости, параллельной некоторой фиксированной плоскости П (рис. 3.1).
Угловая скорость и угловое ускорение твердого тела при плоскопараллельном движении не зависят от выбора полюса. Зная уравнения движения (3.1) точки
Определение вектора скорости произвольной точки плоской фигуры О распределении скоростей точек на отрезке АВ
Как распределены скорости других точек по отрезку

Действительно, если в качестве полюса принять точку 3.6. Чтобы при известных векторах скоростей двух точек Спроектируем уравнение (3.7) на ось Отсюда следует еще одна формула для угловой скорости плоской фигуры:
Определение вектора ускорения произвольной точки плоской фигуры Вопросы для самоконтроля к главе 3.
1.Какое движение твердого тела называется плоскопараллельным или плоским? 2. Запишите уравнения плоскопараллельно движения твердого тела. 3. Из каких простейших движений твердого тела математически «складывается» плоскопараллельное движение? 4. Сформулируйте и поясните теорему о геометрическом сложении скоростей точек плоской фигуры. 5. Запишите уравнения метода проекций для определения скорости произвольной точки плоской фигуры. 6. Какая точка плоской фигуры называется полюсом?
7. Зависят ли угловая скорость и угловое ускорение плоской фигуры от выбора полюса? 8. Как вычисляется скорость произвольной точки плоской фигуры при вращении фигуры относительно полюса в плоскопараллельном движении? 9. Сформулируйте теорему о проекциях векторов скоростей двух точек плоской фигуры на ось, проходящую через эти точки. 10. Что называется мгновенным центром скоростей плоской фигуры 11. Как определяется мгновенный центр скоростей плоской фигуры при известных направлениях векторов скоростей двух точек плоской фигуры? 12. Покажите положение мгновенного центра скоростей для известных Вам частных случаев движения плоской фигуры. 13. Как вычисляется скорость произвольной точки плоской фигуры в плоскопараллельном движении при известном положении мгновенного центра скоростей? 14. Сформулируйте теорему о геометрическом сложении векторов ускорений при плоскопараллельном движении плоской фигуры. Из каких векторов состоит в общем случае вектор ускорения произвольной точки плоской фигуры? 15. Как направлены и как вычисляются величины касательной и нормальной составляющих вектора ускорения произвольной точки, возникающего от вращения плоской фигуры относительно полюса? 16. Запишите уравнения метода проекций для определения ускорения произвольной точки плоской фигуры. 17. Какая точка называется мгновенным центром ускорений плоской фигуры? 18. Как вычисляется ускорение произвольной точки плоской фигуры при известном мгновенном центре ускорений?
ГЛАВА 3. ПЛОСКОПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
§ 3.1. Общие понятия и определения 3.1. Плоскопараллельным или плоским называется такое движение твердого тела, при котором каждая его точка движется в плоскости, параллельной некоторой фиксированной плоскости П (рис. 3.1).
|
|||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 237; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.218.230.170 (0.01 с.) |


 , можно записать уравнения движения точки В плоской фигуры Ф. Пусть
, можно записать уравнения движения точки В плоской фигуры Ф. Пусть  ,
,  – координаты точки В в неподвижной системе координат Оху. Тогда (см. рис. 3.3) будем иметь:
– координаты точки В в неподвижной системе координат Оху. Тогда (см. рис. 3.3) будем иметь: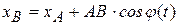 ,
,  (3.6)
(3.6) ? Возьмем произвольную точку С между точками
? Возьмем произвольную точку С между точками  ,
,  ,
,  лежат на одной прямой A1B1.
лежат на одной прямой A1B1. ,
,  . Отсюда
. Отсюда  . Другими словами,
. Другими словами,  . Это означает, что концы векторов скоростей
. Это означает, что концы векторов скоростей  всех точек отрезка
всех точек отрезка  . Отсюда следует, что треугольники
. Отсюда следует, что треугольники  и треугольник
и треугольник  - подобны. Отсюда
- подобны. Отсюда  или
или 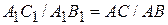 , или
, или  . Следовательно,
. Следовательно, и
и  определить вектор скорости
определить вектор скорости  точки
точки 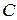 , лежащей между ними, надо в точке С построить вектор
, лежащей между ними, надо в точке С построить вектор  (рис.3.10) и получим:
(рис.3.10) и получим: 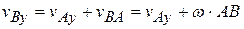
 (3.13)
(3.13)


