
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методика розв’язання задач така ж сама, як попередньому випадку ⇐ ПредыдущаяСтр 8 из 8
При послідовному з’єднанні пружин сумарне зміщення вантажу (розтягнення двох пружин) є сумою їх розтягнень (окремих зміщень від початкового положення)
тому
і, оскільки
то для визначення ефективної жорсткості системи пружин отримуємо
Під дією сили тяжіння пружини будуть деформуватися, а величина статичної деформації
звідки
Відносно цього положення, яке в подальшому вважаємо початком відліку х – координати, будуть здійснюватися коливання. В нашому випадку кругова частота становить а значення величини
Оскільки виконується умова
де
що дозволяє визначити період коливань
і ми отримуємо рівняння згасаючих коливань у вигляді
Знайдемо величини
після чого скористуємось початковими умовами і отримаємо:
Розв’язуючи цю систему рівнянь відносно
Знайдені значення
Таким чином, остаточно рівняння коливань приймає вигляд
Графік цих коливань приведено на рис. 5.5.
Дослідимо максимальні відхилення 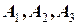 , які відповідають моментам часу , які відповідають моментам часу  , ,  , , 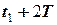 і переконаємося, що і переконаємося, що
тобто утворюють геометричну прогресію зі знаменником 0,73. Відповідь: в) Змушені коливання з одним ступенем свободи Якщо на матеріальну точку масою
(де Складемо диференціальне рівняння руху такого тіла масою
де Розв’язок неоднорідного диференціального рівняння (5.23), як відомо з теорії диференціальних рівнянь, має вигляд де
а З плином часу амплітуда руху, зумовленого вільними коливаннями при наявності сил тертя, згідно (5.16) зменшується практично до нуля, і рух тіла буде визначатися лише зовнішньою силою (5.22). Час установлення режиму вимушених коливань визначається величиною коефіцієнта демпферування Отож, частковий розв’язок рівняння (5.23) знаходять у вигляді
де сталі
Таким чином, амплітуда і фаза змушених коливань при наявності тертя визначаються як властивостями зовнішньої сили (частотою Величина Залежність амплітуди змушених коливань від частоти зовнішньої сили називається амплітудно-частотною характеристикою При
Якщо Максимальна величина амплітуди відповідає так званій резонансній частоті
Таким чином, при
Звернемо увагу на те, що, взагалі Відмітимо, що при зростанні
Що стосується зсуву фаз, то з формули (5.28) випливає, що незалежно від коефіцієнта демпферування Аналізувати амплітудно-частотну криву
Резонансу відповідає значення безрозмірної частоти
при якій відносна амплітуда досягає значення
Зауважимо, що, оскільки Контрольні запитання 1. Сформулюйте умови виникнення змушених коливань. 2. Запишіть диференціальне рівняння змушених коливань. Що необхідно знати для однозначного розв’язку такого рівняння? 3. Запишіть розв’язок диференціального рівняння змушених коливань. 4. Чим визначаються період змушених коливань? 5. Як впливають початкові умови на амплітуду і фазу змушених коливань? 6. Як впливає сила тертя на амплітуду і фазу змушених коливання? 7. За яким законом змінюється амплітуда змушених коливань? Від яких факторів залежить амплітуда змушених коливань? 8. Намалюйте графік залежності амплітуди змушених коливань від частоти збурювальної сили (амплітудно-частотну характеристику змушених коливань) для різних значень сили тертя (коефіцієнта згасання). 9. Намалюйте графік амплітудно-фазової характеристики змушених коливань (графік залежності зсуву фаз між змушеними коливаннями та зовнішньої силою від частоти сили) для різних значень сили тертя (коефіцієнта згасання). 10. Який випадок змушених коливань називається резонансом? Приклад. Тіло масою 1) Записати диференціальне рівняння змушених коливань, знайти значення резонансної частоти, статичне зміщення та амплітуду змушених коливань при резонансі. 2) Побудувати амплітудно-резонансну криву в безрозмірних частотах Розв’язання. Як і раніше, перш за все, знайдемо ефективний коефіцієнт жорсткості двох пружин. В даному прикладі пружини закріплені послідовно, але, на відміну від попереднього прикладу, стискування однієї пружини силою Запишемо диференціальне рівняння вимушених коливань с урахуванням сил тертя
та визначимо сталі, які входять до цього рівняння:
Всі ці величини є необхідними для подальших розрахунків. Так, резонансну частоту коливань визначимо за формулою (5.30)
амплітуду коливань в резонансі обчислимо, користуючись (5.31)
а статичне зміщення – за формулою (5.29)
Ця залежність наведена на рис. 5.7.
Для побудови амплітудно-резонансних кривих в безрозмірних частотах скористуємось виразом (5.32)
Відповідь: Задача ДТ.5. Дослідження одномірних вільних,
Тіло масою 1) Знайти положення рівноваги, відносно якого мають місце коливання. 2) Записати диференціальне рівняння вільних незгасаючих коливань, скласти характеристичне рівняння та розв’язати його для заданих початкових умов 3) Записати диференціальне рівняння згасаючих коливань при наявності сили опору 4) Записати диференціальне рівняння змушених коливань для зовнішньої сили 5) Перейти до безрозмірної частоти Необхідні дані наведені в таблиці ДТ.5. На рис. 1 та 4 точка закріплення діліть відстань між пружинами у відношенні обернено пропорційному їх жорсткостям. Тіло здійснює коливання вздовж вертикалі (рис. 1 та 2) чи вздовж похилої площини (рис. 3 – 6).
Таблиця ДТ.5 – вихідні дані для задачі ДТ.5
Закінчення таблиці ДТ.5.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 166; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.19.31.73 (0.066 с.) |
 Приклад. Знайти рівняння коливань тіла масою
Приклад. Знайти рівняння коливань тіла масою  = 0,6 кг, яке прикріплене до двох послідовно з’єднаних пружин жорсткістю
= 0,6 кг, яке прикріплене до двох послідовно з’єднаних пружин жорсткістю 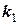 = 150 Н/м та
= 150 Н/м та  = 100 Н/м (рис. 5.4) якщо сила опору
= 100 Н/м (рис. 5.4) якщо сила опору  , а початкові умови
, а початкові умови  = 0,2 м,
= 0,2 м,  = 2 м/с.
= 2 м/с. ,
,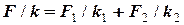 ,
,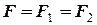 ,
,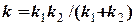 = 150·100/250 = 60 Н/м.
= 150·100/250 = 60 Н/м. може бути знайдена з умови
може бути знайдена з умови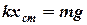 ,
,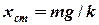 = 0,6·10/60 = 0,1 м.
= 0,6·10/60 = 0,1 м. =
= 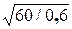 = 10 рад/с.
= 10 рад/с.
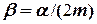 = 0,5 с-1.
= 0,5 с-1. , то
, то ,
, = 9,99 рад/с,
= 9,99 рад/с, = 0,629 с,
= 0,629 с,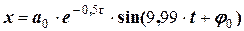 .
. та
та  з початкових умов. Спочатку знайдемо вираз для швидкості (взявши похідну від зміщення)
з початкових умов. Спочатку знайдемо вираз для швидкості (взявши похідну від зміщення) ,
, ,
, = 2,0 =
= 2,0 =  .
.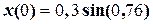 = 0,2 м =
= 0,2 м = 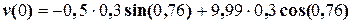 = 2,0 м/с =
= 2,0 м/с =  м.
м.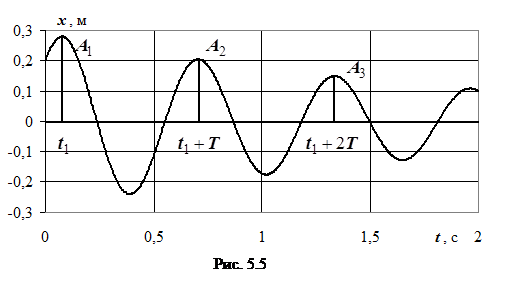
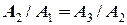 = … =
= … =  = 0,73
= 0,73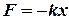 та сили в’язкого тертя
та сили в’язкого тертя 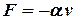 , діє збурювальна (зовнішня) сила, яка змінюється за гармонічним законом
, діє збурювальна (зовнішня) сила, яка змінюється за гармонічним законом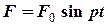 , (5.22)
, (5.22)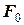 – амплітуда збурювальної сили,
– амплітуда збурювальної сили, 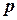 – її частота), то рух, який буде здійснювати точка, називається змушеними коливаннями.
– її частота), то рух, який буде здійснювати точка, називається змушеними коливаннями.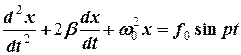 , (5.23)
, (5.23) , а
, а 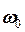 такі ж самі, як і раніше (дивись формулу (5.10)).
такі ж самі, як і раніше (дивись формулу (5.10)).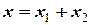 , (5.24)
, (5.24) – загальний розв’язок однорідного рівняння (5.23) нам вже відомий (дивись формулу (5.16)), отож
– загальний розв’язок однорідного рівняння (5.23) нам вже відомий (дивись формулу (5.16)), отож , (5.25)
, (5.25)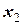 – будь-який частковий розв’язок неоднорідного рівняння (5.23).
– будь-який частковий розв’язок неоднорідного рівняння (5.23).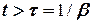 можна розглядати лише усталені змушені коливання для яких початкові умови вже не мають ніякого значення.
можна розглядати лише усталені змушені коливання для яких початкові умови вже не мають ніякого значення.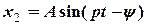 , (5.26)
, (5.26) та
та 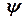 отримують після підстановки функції (5.26) та її похідних в рівняння (5.23) та певних алгебраїчних перетворень:
отримують після підстановки функції (5.26) та її похідних в рівняння (5.23) та певних алгебраїчних перетворень: , (5.27)
, (5.27)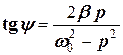 . (5.28)
. (5.28) та коефіцієнтом демпфірування
та коефіцієнтом демпфірування 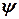 , яка входить до розв’язку (5.26) зветься зсувом фаз і визначає різницю між фазою коливань і фазою зовнішньої сили (5.22) в даний момент часу.
, яка входить до розв’язку (5.26) зветься зсувом фаз і визначає різницю між фазою коливань і фазою зовнішньої сили (5.22) в даний момент часу. , а залежність зсуву фаз від частоти зовнішньої сили – фазово-частотною характеристикою
, а залежність зсуву фаз від частоти зовнішньої сили – фазово-частотною характеристикою 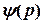 .
.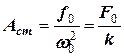 . (5.29)
. (5.29)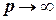 , то
, то 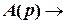 0 за законом
0 за законом 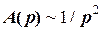 згідно формулі (5.27).
згідно формулі (5.27). яка може бути знайдена з умови мінімуму знаменника формули (5.27)
яка може бути знайдена з умови мінімуму знаменника формули (5.27)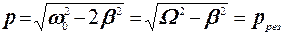 . (5.30)
. (5.30) >
> 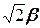 на залежності
на залежності  . (5.31)
. (5.31) <
<  .
.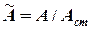 , частоти
, частоти  та параметра згасання
та параметра згасання  . Тоді з формул (5.27) та (5.29) отримуємо вираз для відносної (безрозмірної) амплітуди
. Тоді з формул (5.27) та (5.29) отримуємо вираз для відносної (безрозмірної) амплітуди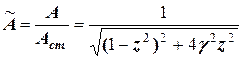 . (5.32)
. (5.32) , (5.33)
, (5.33)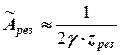 . (5.34)
. (5.34)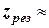 1 для
1 для 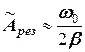 і в реальних ситуаціях резонансна амплітуда коливань може у десятки разів перевищувати статичне зміщення.
і в реальних ситуаціях резонансна амплітуда коливань може у десятки разів перевищувати статичне зміщення. вальної сили
вальної сили  при наявності сили опору
при наявності сили опору  Н.
Н.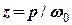 в інтервалі (0; 2,0) для відносної (безрозмірної) амплітуди
в інтервалі (0; 2,0) для відносної (безрозмірної) амплітуди 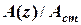 .
.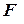 супроводжується розтягом другої пружини з такою ж силою, тому
супроводжується розтягом другої пружини з такою ж силою, тому 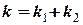 = 200 Н/м.
= 200 Н/м.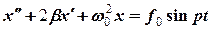 ,
,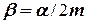 = 0,8/(2·0,5) = 0,8 рад/с,
= 0,8/(2·0,5) = 0,8 рад/с, = 14/0,5 = 28 м/с2.
= 14/0,5 = 28 м/с2.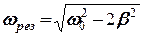 =
=  = 19,9 рад/с,
= 19,9 рад/с, = 0,88 м,
= 0,88 м, = 28/400 = 0,07 м.
= 28/400 = 0,07 м.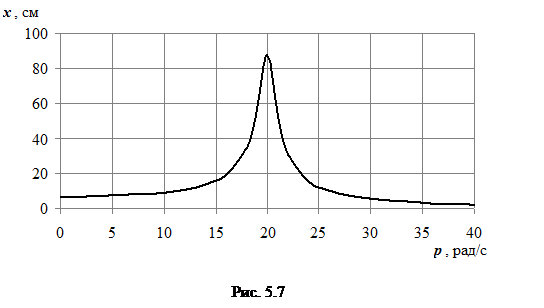

 , та будуємо відповідний графік (рис. 5.8).
, та будуємо відповідний графік (рис. 5.8).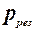 = 19,9 рад/с,
= 19,9 рад/с, 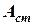 = 0,07 м,
= 0,07 м, 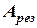 = 0,88 м.
= 0,88 м.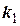 і
і 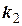 (рис. 1 - 6).
(рис. 1 - 6).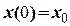 ,
,  . Визначити початкову фазу
. Визначити початкову фазу  , частоту
, частоту 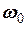 , та амплітуду
, та амплітуду 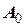 таких коливань. Побудувати графік коливань протягом трьох періодів.
таких коливань. Побудувати графік коливань протягом трьох періодів. , та розв’язати його для тих самих початкових умов. Визначити початкову фазу
, та розв’язати його для тих самих початкових умов. Визначити початкову фазу 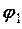 , частоту
, частоту  , початкову амплітуду
, початкову амплітуду  і декремент згасання. Користуючись ПЕОМ побудувати графік згасаючих коливань протягом трьох періодів та визначити з графіка декремент згасання.
і декремент згасання. Користуючись ПЕОМ побудувати графік згасаючих коливань протягом трьох періодів та визначити з графіка декремент згасання.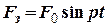 з урахуванням сили опору
з урахуванням сили опору 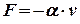 . Записати загальний розв’язок цього рівняння. Записати вираз для амплітуди та фази змушених коливань. Визначити статичне зміщення, резонансну частоту і амплітуду коливань в резонансі.
. Записати загальний розв’язок цього рівняння. Записати вираз для амплітуди та фази змушених коливань. Визначити статичне зміщення, резонансну частоту і амплітуду коливань в резонансі.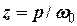 та, користуючись ПЕОМ, побудувати амплітудно-резонансну криву
та, користуючись ПЕОМ, побудувати амплітудно-резонансну криву  в інтервалі
в інтервалі 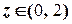 .
.

 3
3
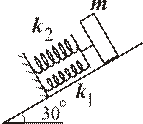
 5
5

 , Н/м
, Н/м
 , Н/м
, Н/м
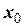 , м
, м
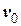 , м/с
, м/с
 , кг/с
, кг/с
 , Н
, Н



