
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методика розв’язання задач для сталих сил.Содержание книги
Поиск на нашем сайте 1) Визначаємо всі сили, що діють на точку. 2) Записуємо диференціальне рівняння руху точки під дією сил, головний вектор яких позначимо
3) Вибираємо систему координат, зручну для умов задачі, та записуємо диференціальні рівняння в проекціях на осі. У випадку декартових координат маємо:
4) Якщо точка рухається по колу, то доцільно користуватися циліндричною або полярною системою координат з початком у центрі кола. 5) Послідовно інтегруємо диференціальні рівняння, визначаючи сталі інтегрування з початкових умов і отримуємо рівняння руху точки. 6) З отриманого закону руху визначаємо величини, які необхідно знайти. Приклад. Тіло рухається з точки
Опором повітря та розмірами тіла нехтувати. Розв’язання. Розглянемо рух тіла по похилій площині. На нього діють сили: вага
Задача двомірна, оскільки рух як на першій, так і на другій ділянці відбувається в площині рисунка. Розташуємо початок декартової системи координат
отже
де
Інтегруючи двічі диференціальне рівняння (4), отримуємо:
Для визначення сталих інтегрування
і отримуємо:
Тоді, остаточно, для координати тіла
Ці рівняння дозволяють визначити швидкість тіла
Далі розглянемо рух тіла від точки
Розташуємо початок нової декартової системи координат
отже:
Початкові умови на цій ділянці наступні:
та
Двічі інтегруємо диференціальні рівняння (10) і послідовно отримаємо:
та
Запишемо отримані рівняння для моменту часу
та
Таким чином, рівняння для визначення координат та компонентшвидкості тіла на другій ділянці руху набувають вигляду:
та
Координату точки падіння тіла на площину визначимо з умови (дивись рис. 2.1)
Тоді рівняння (15) приймає вигляд
що дозволяє визначити час Т, протягом якого тіло рухається на ділянці
Тоді з (12) та (14) знаходимо компоненти швидкості тіла в момент падіння:
що дозволяє визначити модуль швидкості в точці падіння
та кут
що дає Відповідь: Задача ДТ.2. Визначення параметрів закону руху
При розв’язку задачі мотоцикл з мотоциклістом вважати матеріальною точкою, нехтувати тертям кочення та силою опору повітря. Згідно з варіантом знайти невідомі параметри. Варіант № 1. Дано: Варіант № 4. Дано: Варіант № 7. Дано: Варіант № 10. Дано: Варіант № 13. Дано: Варіант № 16. Дано: Варіант № 19. Дано: Варіант № 22. Дано: Варіант № 25. Дано: Варіант № 28. Дано:
При розв’язку задачі тіло вважати матеріальною точкою масою Варіант № 2. Дано: Варіант № 5. Дано: Варіант № 8. Дано: Варіант № 11. Дано: Варіант № 14. Дано: Варіант № 17. Дано: Варіант № 20. Дано: Варіант № 23. Дано: Варіант № 26. Дано: Варіант № 29. Дано:
При розв’язку задачі тіло вважати матеріальною точкою масою Варіант № 3. Дано: Варіант № 6. Дано: Варіант № 9. Дано: Варіант № 12. Дано: Варіант № 15. Дано: Варіант № 18. Дано: Варіант № 21. Дано: Варіант № 24. Дано: Варіант № 27. Дано: Варіант № 30. Дано: § 3. Обернена задача динаміки. Визначення закону руху
|
||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 291; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.126 (0.019 с.) |


 .
. ,
, ,
, .
. похилої площини маючи початкову швидкість
похилої площини маючи початкову швидкість  = 12 м/с. Кут нахилу площини до горизонту
= 12 м/с. Кут нахилу площини до горизонту  = 30º, коефіцієнт тертя ковзання
= 30º, коефіцієнт тертя ковзання  = 0,1. Через
= 0,1. Через  = 0,5 с тіло покидає похилу площину і падає на горизонтальну площину в точці
= 0,5 с тіло покидає похилу площину і падає на горизонтальну площину в точці  (рис. 2.1).
(рис. 2.1).
 похилої площини, швидкість точки
похилої площини, швидкість точки  в кінці похилої площини, а також координати (
в кінці похилої площини, а також координати ( ) точки падіння, швидкість тіла
) точки падіння, швидкість тіла  в момент падіння тіла на горизонтальну площину та кут падіння
в момент падіння тіла на горизонтальну площину та кут падіння  .
. , нормальнареакція
, нормальнареакція  та сила тертя ковзання
та сила тертя ковзання  . Диференціальне рівняння руху тіла на першій ділянці має вигляд
. Диференціальне рівняння руху тіла на першій ділянці має вигляд . (1)
. (1)
 в точці
в точці  (рис. 2.1), і з рівняння (1) отримуємо відповідні скалярні рівняння, які визначають рух тіла по похилій площині:
(рис. 2.1), і з рівняння (1) отримуємо відповідні скалярні рівняння, які визначають рух тіла по похилій площині: , (2)
, (2) , (3)
, (3) . Оскільки
. Оскільки  , перепишемо (2) з врахуванням (3) в наступному вигляді
, перепишемо (2) з врахуванням (3) в наступному вигляді , (4)
, (4) = 6,0 м/с.
= 6,0 м/с. ,
, .
. , та
, та  скористуємося початковими умовами:
скористуємося початковими умовами: (0) = 0,
(0) = 0, ,
, на першому етапі руху маємо:
на першому етапі руху маємо: , (5)
, (5) . (6)
. (6)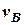 =
=  = –6·0,5 + 12 = 9 м/с, (7)
= –6·0,5 + 12 = 9 м/с, (7) м. (8)
м. (8) до точки падіння
до точки падіння 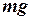 тому диференціальне рівняння руху має вигляд
тому диференціальне рівняння руху має вигляд . (9)
. (9) в точці
в точці  , (10)
, (10) , (11)
, (11) ,
, .
. ,
,  = 7,8 м/с,
= 7,8 м/с, = 0,
= 0,  = 4,5 м/с.
= 4,5 м/с. =
=  ,
,  ,
, ,
,  .
. = 0 і знайдемо з них сталі інтегрування:
= 0 і знайдемо з них сталі інтегрування: = 7,8 м/с,
= 7,8 м/с,  = 0 м
= 0 м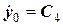 = 4,5 м/с,
= 4,5 м/с,  = 0 м.
= 0 м. м/с, (12)
м/с, (12) м,(13)
м,(13) м/с, (14)
м/с, (14) м. (15)
м. (15) = –2,6 м.
= –2,6 м. ,
, . Розв’язок дає
. Розв’язок дає  = 1,3 с,
= 1,3 с, 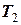 = – 0,4 с. Фізичний зміст має лише корінь
= – 0,4 с. Фізичний зміст має лише корінь  - координату точки падіння тіла
- координату точки падіння тіла м. (16)
м. (16) = 7,8 м/с,
= 7,8 м/с,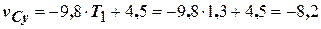 м/с,
м/с,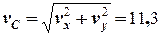 м/с (17)
м/с (17) ,
, = 5,25 м,
= 5,25 м,  м/с,
м/с,  м,
м,  м,
м,  м/с,
м/с,  Варіанти 1, 4, 7, 10, 13, 16, 19, 22, 25, 28: Мотоцикл під дією сталої сили
Варіанти 1, 4, 7, 10, 13, 16, 19, 22, 25, 28: Мотоцикл під дією сталої сили  піднімається
піднімається  . В точці
. В точці  і через
і через  с приземляється в точці
с приземляється в точці  .
. = 0;
= 0;  = 40 м;
= 40 м;  та
та  .
. 0;
0; 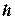 .
. Варіанти 2, 5, 8, 11, 14, 17, 20, 23, 26, 29: Тіло рухається з точки
Варіанти 2, 5, 8, 11, 14, 17, 20, 23, 26, 29: Тіло рухається з точки  та
та  Варіанти 3, 6, 9, 12, 15, 18, 21, 24, 27, 30: Лижник, опускаючись з вершини трампліна та підходить до точки
Варіанти 3, 6, 9, 12, 15, 18, 21, 24, 27, 30: Лижник, опускаючись з вершини трампліна та підходить до точки  = 8 м;
= 8 м;  .
.


