
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Відносний рух точки. Сили інерції
де Нехай інша система відліку (
де Підставляючи рівняння (4.2) в (4.1) отримуємо
Перепишемо рівняння (4.3) для спостерігача, що знаходиться в неінерціальній системі, у такому вигляді, щоб воно мало такий самий вигляд, як і в інерціальній
в якому
Рівняння (4.4) описує відносний рух точки. Таким чином, для опису руху в рухомій системі до результуючої зовнішніх сил
сила інерції Коріоліса. Таким чином, сили інерції обумовлюють різницю між відносним і абсолютним прискореннями і вибирають їх такими, щоб вони забезпечували в неінерціальній системі відліку ті прискорення, які фактично мають місце для спостерігача, який знаходиться в цій неінерціальній системі. Нагадаємо що, в загальному випадку прискорення переносного руху може складатися з трьох доданків
які зумовлені поступальним рухом неінерціальної системи Сили інерції залежать від: 1. Властивостей неінерціальної системи - від прискорення поступального руху системи
Перший доданок
зумовлений прискореним поступальним рухом системи - така сила виникає при гальмуванні або прискоренні судна, коли нас „відкидає” у напряму, протилежному прискоренню. Другий доданок
називають відцентровою силою, бо ця сила напрямлена вздовж радіуса обертання від осі обертання – у протилежну сторону від нормального прискорення – і діє на матеріальну точку. Прояв відцентрової сили ми відчуваємо при зміні напряму руху: при правому повороті нас відкидає вліво і навпаки.
Виникнення сил інерції у випадку обертального руху широко застосовується в техніці: регулятор кількості обертів, сепаратор тощо. Останній доданок
називається обертальною силою інерції, яка виникає при зміні кутової швидкості обертання системи (переносника) - ця сила напрямлена проти тангенціального прискорення. Прояв сили нерівномірного обертання ми відчуваємо коли карусель набирає оберти або гальмує, тоді ми або притискаємося до спинки сидіння, або від неї відриваємося. 2. Від властивостей системи та тіла - якщо рухома система здійснює обертальний рух з кутовою швидкістю
Прояв сили Коріоліса в умовах Землі приводить до зміни напряму морських течій – праворуч в північній півкулі та ліворуч в південній. Контрольні запитання 1. Які системи відліку називаються неінерціальними? Чи виконується в таких системах відліку закони Ньютона? 2. Запишіть другий закон Ньютона для відносного руху. Наведіть приклади, коли він проявляється. Чим зумовлена поява сил інерції в рухомій системі? 3. Як визначається сила інерції в неінерціальній системі відліку, що рухається поступально? 4. Яка сила інерції виникає в системі відліку, що здійснює обертальний рух зі сталою кутовою швидкістю, якщо тіло в цій системі нерухоме? 5. Які сили інерції виникають в системі відліку, що здійснює нерівномірний обертальний рух, якщо тіло в цій системі нерухоме? 6. Чому дорівнює переносна сила інерції? В яких випадках вона дорівнює нулю? 7. Поясніть причину виникнення сили інерції Коріоліса. 8. Чому дорівнює сила інерції Коріоліса? В яких випадках вона дорівнює нулю? 9. В якому випадку диференціальні рівняння відносного та абсолютного руху точки співпадають? 10. Які сили інерції проявляються в умовах Землі? 11. Як повинно рухатися судно з незмінним значенням швидкості, щоб сила інерції Коріоліса дорівнювала нулю?
12. Як повинно рухатися судно з незмінним значенням швидкості, щоб сила інерції Коріоліса була максимальною? Методика розв’язання задач 1. Визначити з умов задачі яке з тіл є переносником, а яке рухається по ньому. 2. Умовно зупинити рух переносника та визначити особливості траєкторії відносного руху, положення рухомого тіла та його швидкість 3. Умовно зупинити відносний рух тіла в заданий момент часу та визначити особливості траєкторії переносного руху, прискорення 4. Якщо 5. За правилами складання векторів визначити силу інерції. 6. Записати рівняння відносного руху точки та знайти його розв’язок.
В цей момент двигун механізму відключають, а момент зовнішніх сил забезпечує рівномірне обертання системи (трубка та механізм) з досягнутим значенням кутової швидкості. Знайти закон руху механізму по трубі, нехтуючи силами тертя. Розв’язання. Рівняння відносного руху механізму
в якому
та силу інерції Коріоліса
Отже рівняння (1) приймає вигляд
Для знаходження сил інерції, згідно рівнянням (3) та (4), нам треба визначити положення механізму Знайдемо положення механізму М в трубці в даний момент часу, підставляючи цей час в рівняння його відносного руху
Таким чином, вектор
Для моменту часу Кутову швидкість обертального руху диску
і, підставляючи
Від’ємне значення кутової швидкості означає, що обертання трубки здійснюється за рухом стрілки годинника і вектор кутової швидкості Кутове прискорення обертального (переносного) руху ε е знайдемо як похідну по часу від кутової швидкості
що, після підстановки вказаного моменту часу, дає
Додатне значення кутового прискорення вказує, що вектор кутового прискорення диску
Визначаємо модулі всіх сил інерції. Оскільки
модуль відцентрової сили
та модуль сили інерції Коріоліса
Напрями всіх сил інерції визначимо за правилами визначення напряму вектора при векторному добутку складових та вкажемо їх на рис. 4.4. Запишемо тепер рівняння (4), яке описує відносний рух механізму у наступні моменти часу. Оскільки на механізм сила тяги перестала діяти, тобто
Складаємо характеристичне рівняння:
Корені цього рівняння будуть
Сталі інтегрування
тоді отримуємо маємо систему рівнянь:
звідки знаходимо:
що з врахуванням умов задачі дає:
Отже
Відповідь: у момент часу
|
|||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 311; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.175.180 (0.037 с.) |
 Розглянемо рух точки по відношенню до двох систем відліку з загальнім відліком часу. Виберемо інерціальну нерухому систему відліку (
Розглянемо рух точки по відношенню до двох систем відліку з загальнім відліком часу. Виберемо інерціальну нерухому систему відліку ( ) і назвемо її абсолютною (рис. 4.1). В цій системі другий закон Ньютона виконується і має вигляд
) і назвемо її абсолютною (рис. 4.1). В цій системі другий закон Ньютона виконується і має вигляд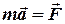 , (4.1)
, (4.1) - прискорення точки відносно інерціальної системи (абсолютне прискорення),
- прискорення точки відносно інерціальної системи (абсолютне прискорення),  - результуюча сила, яка діє на точку М.
- результуюча сила, яка діє на точку М. ) – її називають переносником, рухається відносно даної інерціальної (
) – її називають переносником, рухається відносно даної інерціальної ( рухається з відносним прискоренням
рухається з відносним прискоренням  . Прискорення точки в абсолютній
. Прискорення точки в абсолютній  , (4.2)
, (4.2) – прискорення, яке має точка в переносному русі,
– прискорення, яке має точка в переносному русі,  - прискорення Коріоліса.
- прискорення Коріоліса. . (4.3)
. (4.3)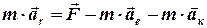 =
= 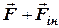 , (4.4)
, (4.4) . (4.5)
. (4.5)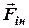 (дивись рис. 4.2), яка може мати дві складові
(дивись рис. 4.2), яка може мати дві складові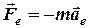 (4.6)
(4.6)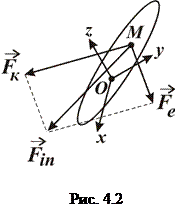 так звана переносна сила інерції та
так звана переносна сила інерції та (4.7)
(4.7) , (4.8)
, (4.8) та обертальним рухом цієї системи (доданки
та обертальним рухом цієї системи (доданки  =
=  та
та  =
=  описані в
описані в  та кутової швидкості
та кутової швидкості 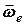
 . (4.9)
. (4.9) , (4.10)
, (4.10) , (4.11)
, (4.11) , (4.12)
, (4.12) , а тіло в ній рухається з відносною швидкістю
, а тіло в ній рухається з відносною швидкістю  , то виникає сила інерції Коріоліса
, то виникає сила інерції Коріоліса =
=  . (4.13)
. (4.13) тієї точки переносника, в якій знаходиться рухоме тіло в даний момент часу, та відповідні складові сил інерції.
тієї точки переносника, в якій знаходиться рухоме тіло в даний момент часу, та відповідні складові сил інерції. ≠ 0 та
≠ 0 та  Приклад 1. Горизонтальна трубка
Приклад 1. Горизонтальна трубка  починає обертатися навколо вертикальної осі (рис. 4.3) за законом
починає обертатися навколо вертикальної осі (рис. 4.3) за законом  (рад). Одночасно механізм М масою
(рад). Одночасно механізм М масою  = 0,2 кг починає рух вздовж трубки за законом відносного руху
= 0,2 кг починає рух вздовж трубки за законом відносного руху  = ОМ =
= ОМ = 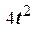 (см). Вважаючи механізм матеріальною точкою, визначити сили інерції, які діють на нього на момент часу
(см). Вважаючи механізм матеріальною точкою, визначити сили інерції, які діють на нього на момент часу  = 2 c та зобразити їх на рисунку. Записати рівняння відносного руху матеріальної точки М.
= 2 c та зобразити їх на рисунку. Записати рівняння відносного руху матеріальної точки М. , (1)
, (1) , (2)
, (2) . (4)
. (4) ), його відносну швидкість
), його відносну швидкість  , кутову швидкість
, кутову швидкість  = ОМ = 4·22 = 16 см.
= ОМ = 4·22 = 16 см.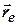 відносного положення механізму М спрямований вздовж трубки та має модуль 16 см (рис. 4.4 а – вид на горизонтальну площину, рис. 4.4 б - вид на фронтальну площину).
відносного положення механізму М спрямований вздовж трубки та має модуль 16 см (рис. 4.4 а – вид на горизонтальну площину, рис. 4.4 б - вид на фронтальну площину). Знайдемо відносну швидкість механізму М як першу похідну від рівняння відносного руху за часом
Знайдемо відносну швидкість механізму М як першу похідну від рівняння відносного руху за часом =
= 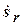 =
=  .
. знайдемо як першу похідну кута повороту диска за часом
знайдемо як першу похідну кута повороту диска за часом =
= 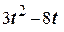 ,
,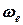 = 3·22 – 8·2 = – 4 рад/с.
= 3·22 – 8·2 = – 4 рад/с. =
= 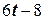 ,
,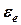 = 4 рад/с2.
= 4 рад/с2. ,
, 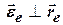 , та
, та  , послідовно знайдемо модуль обертальної сили інерції
, послідовно знайдемо модуль обертальної сили інерції = 0,2·4·0,16 = 0,128 Н, (5)
= 0,2·4·0,16 = 0,128 Н, (5) = 0,2·42·0,16 = 0,512 Н, (6)
= 0,2·42·0,16 = 0,512 Н, (6) = 2·0,2·4·0,16·1 = 0,256 Н. (7)
= 2·0,2·4·0,16·1 = 0,256 Н. (7) = 0, а рух точки здійснюється лише вздовж прямої
= 0, а рух точки здійснюється лише вздовж прямої  (рис. 4.5) набуває вигляду
(рис. 4.5) набуває вигляду .
. Розв’язуємо дане диференціальне рівняння де кутова швидкість стала і дорівнює
Розв’язуємо дане диференціальне рівняння де кутова швидкість стала і дорівнює 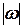 = 4 рад/с з початковими умовами для нового початку відліку часу (t = 0 c):
= 4 рад/с з початковими умовами для нового початку відліку часу (t = 0 c):  = 16 см та
= 16 см та  = 16 см/с.
= 16 см/с. = 0.
= 0. , тому загальний розв’язок рівняння буде мати вигляд
, тому загальний розв’язок рівняння буде мати вигляд .
. та
та  знаходимо з початкових умов: спочатку визначимо швидкість точки
знаходимо з початкових умов: спочатку визначимо швидкість точки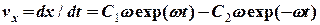 ,
, ,
, ,
, ,
,  ,
, = 0,1 м,
= 0,1 м,  = 0,06 м.
= 0,06 м. м.
м.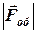 = 0,128 Н,
= 0,128 Н,  = 0,512 Н,
= 0,512 Н, 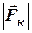 = 0,256 Н; після цього (з новим відліком часу) точка рухається за законом
= 0,256 Н; після цього (з новим відліком часу) точка рухається за законом 


