Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Приклад 2. Визначення закону руху точки, коли на неї діє сила, що залежить лише від швидкості.Содержание книги
Поиск на нашем сайте
Знайти закон руху точки масою m = 0,5 кг, на яке діє сила Розв’язання. Поділивши силу на масу точки отримуємо
Розділяємо змінні в цьому диференціальному рівнянні (обидві частини множимо на
Інтегрування останнього рівняння дає
Сталу інтегрування знаходимо з початкових умов: при t = 0
Таким чином,
і дозволяє визначити залежність швидкості від часу
Перепишемо останнє рівняння у вигляді
Розділяючи змінні та проводячи повторне інтегрування отримаємо
Використовуючи початкову умову
звідки визначаємо другу сталу інтегрування
Тоді остаточно закон руху точки набуває вигляду
Відповідь: Приклад 3. Визначення закону руху точки, коли на неї діє сила, що залежить лише від координати. Знайти закон руху точки масою Розв’язання. Диференціальне рівняння руху точки можна записати згідно (3.3) у вигляді
тоді
Інтегруючи останній вираз
отримуємо зв’язок швидкості з координатою
Підставляючи початкові умови, визначимо
Розділяючи змінні в останньому рівнянні, яке визначає зв’язок між швидкістю та координатою, отримуємо
Після наступного інтегрування дістанемо
звідки початкові умови дозволяють визначити
З останнього виразу отримуємо закон руху у вигляді
Відповідь: Задача ДТ.3. Визначення законуруху матеріальної точки а) сила залежить лише від часу Знайти закон руху матеріальної точки, маса якої Таблиця ДТ.3.а. - вихідні дані для виконання задачі ДТ.3.а.
Закінчення таблиці ДТ.3.а
б) сила залежить лише від координати Знайти закон руху матеріальної точки масою Таблиця ДТ.3.б – вихідні дані для задачі ДТ.3.б.
Закінчення таблиці ДТ.3.б
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 153; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.12.30 (0.006 с.) |

 Н. Цей випадок відповідає ламінарному руху тіла у в’язкому середовищі. Початкові умови: при t = 0 c,
Н. Цей випадок відповідає ламінарному руху тіла у в’язкому середовищі. Початкові умови: при t = 0 c,  = 2 м/с та
= 2 м/с та  = 1 м.
= 1 м. .
. та ділимо на
та ділимо на 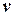 ) і отримуємо
) і отримуємо .
.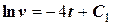 .
. .
. , що дає
, що дає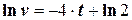 ,
, м/с.
м/с.
 .
. .
. ,
, = 1,5 м.
= 1,5 м. м.
м. = 1 кг, під дією сили
= 1 кг, під дією сили  Н, для початкових умов
Н, для початкових умов  ,
, .
. ,
, .
. = 0. Отож
= 0. Отож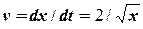 .
.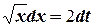 .
. ,
, .
.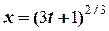 м.
м.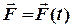 та початковими умовами, які приведені у таблиці ДТ.3.а.
та початковими умовами, які приведені у таблиці ДТ.3.а. ,
кг
,
кг
 , H
, H
 ,
м
,
м
 ,
м/с
,
м/с
 , H
, H
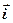


 Н та початковими умовами, які приведені у таблиці ДТ.3.б.
Н та початковими умовами, які приведені у таблиці ДТ.3.б. , Н
, Н