
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методика розв’язання прямої задачі динамікиСтр 1 из 8Следующая ⇒
РОЗДІЛ ІІІ. ДИНАМІКА Динаміка є частиною теоретичної механіки, в якій вивчається рух тіл як результат їх взаємодії. Основи динаміки були закладені Ньютоном, який узагальнив накопичені до нього досліди по руху тіл і сформулював три основні закони механіки, які відомі з курсу фізики. Динаміку розділяють на дві частини: динаміку матеріальної точки, де вивчають рух тіла, розмірами якого можна нехтувати в конкретній задачі та динаміку механічної системи – сукупності матеріальних точок, положення та рух кожної з яких залежить від положення та руху усіх останніх. ЧАСТИНА І. ДИНАМІКА ТОЧКИ Пряма задача динаміки Пряма (перша) задача динаміки – визначити рівнодійну сил 1. Якщо закон руху матеріальної точки задано векторним способом
який еквівалентний трьом скалярним рівнянням:
то задача розв’язується однозначно шляхом подвійного диференціювання рівнянь руху. Дійсно, швидкість визначиться як перша похідна закону руху за часом
Дійсно, визначивши
(тут З останнього рівняння випливає, що сила
Контрольні запитання 1. Сформулюйте перший закон Ньютона. Наведіть приклади. 2. Які системи відліку називаються інерціальними? 3. Сформулюйте принцип відносності Галілея. 4. Яка фізична величина є мірою інертності тіла? 5. Якою фізичною величиною характеризується зміна стану спокою або руху тіла зі сталою швидкістю? 6. Сформулюйте другий закон Ньютона. 7. Сформулюйте третій закон Ньютона. 8. Сформулюйте першу задачу динаміки. Як вона розв’язується коли закон руху матеріальної точки задано векторним (координатним) способом?
9. Як розв’язується перша задача динаміки коли рівняння руху матеріальної точки задано у натуральній формі? Методика розв’язання задач 1. Визначити з умов задачі яке з тіл є переносником, а яке рухається по ньому. 2. Умовно зупинити рух переносника та визначити особливості траєкторії відносного руху, положення рухомого тіла та його швидкість 3. Умовно зупинити відносний рух тіла в заданий момент часу та визначити особливості траєкторії переносного руху, прискорення 4. Якщо 5. За правилами складання векторів визначити силу інерції. 6. Записати рівняння відносного руху точки та знайти його розв’язок.
В цей момент двигун механізму відключають, а момент зовнішніх сил забезпечує рівномірне обертання системи (трубка та механізм) з досягнутим значенням кутової швидкості. Знайти закон руху механізму по трубі, нехтуючи силами тертя. Розв’язання. Рівняння відносного руху механізму
в якому
та силу інерції Коріоліса
Отже рівняння (1) приймає вигляд
Для знаходження сил інерції, згідно рівнянням (3) та (4), нам треба визначити положення механізму
Знайдемо положення механізму М в трубці в даний момент часу, підставляючи цей час в рівняння його відносного руху
Таким чином, вектор
Для моменту часу Кутову швидкість обертального руху диску
і, підставляючи
Від’ємне значення кутової швидкості означає, що обертання трубки здійснюється за рухом стрілки годинника і вектор кутової швидкості Кутове прискорення обертального (переносного) руху ε е знайдемо як похідну по часу від кутової швидкості
що, після підстановки вказаного моменту часу, дає
Додатне значення кутового прискорення вказує, що вектор кутового прискорення диску Визначаємо модулі всіх сил інерції. Оскільки
модуль відцентрової сили
та модуль сили інерції Коріоліса
Напрями всіх сил інерції визначимо за правилами визначення напряму вектора при векторному добутку складових та вкажемо їх на рис. 4.4. Запишемо тепер рівняння (4), яке описує відносний рух механізму у наступні моменти часу. Оскільки на механізм сила тяги перестала діяти, тобто
Складаємо характеристичне рівняння:
Корені цього рівняння будуть
Сталі інтегрування
тоді отримуємо маємо систему рівнянь:
звідки знаходимо:
що з врахуванням умов задачі дає:
Отже
Відповідь: у момент часу Механічні коливання а) Вільні незгасаючі коливання з одним ступенем свободи Малі коливання, які здійснює матеріальна точка масою
з початковими умовами:
де Зауважимо, що дія сталої сили на точку, яка здійснює коливання, змінює лише положення рівноваги, тобто точку, відносно якої здійснюються коливання, але не змінює рівняння коливань. Тому дія на точку сталої сили не впливає на результат розв’язку рівняння.
Характеристичне рівняння для однорідного диференціального рівняння зі сталими коефіцієнтами (5.1) має вигляд Корені цього рівняння чисто уявні (
в якому Це рівняння, за допомогою перетворень Ейлера зводиться до вигляду
в якому сталі коефіцієнти
Рівняння (5.3), в свою чергу, зводиться до однієї гармонічної функції
Коливання, які здійснюються за законом (5.3) чи (5.4) називаються гармонічними, але закон (5.4) аналізувати значно легше, ніж (5.3). Величина Сталі інтегрування
Звернемо увагу, що при визначенні початкової фази
і необхідно знайти значення Контрольні запитання 1. Сформулюйте умови виникнення коливань. 2. Як спрямована сила, що викликає гармонічні коливання? Чи існують в природі такі сили? Наведіть приклади. 3. Запишіть диференціальне рівняння коливального руху. Що необхідно знати для однозначного розв’язку такого рівняння? 4. Як отримати розв’язок такого рівняння? 5. Запишіть розв’язок диференціального рівняння коливального руху. Що таке період та амплітуда коливань? 6. Від чого залежить період (частота) коливань та амплітуда коливань? 7. Як впливає стала сила, що діє на матеріальну точку, на її коливання? Методика розв’язання задач 1. Визначити ефективний коефіцієнт жорсткості пружин. 2. Визначити положення рівноваги тіла. 3. Записати диференціальне рівняння руху та скласти відповідне характеристичне рівняння. 4. Розв’язати характеристичне рівняння та проаналізувати його корені. 5. Скористатися перетворенням Ейлера та визначити гармонічну функцію. 6. Знайти сталі інтегрування, користуючись початковими умовами. Приклад. Тіло масою
тому ефективна жорсткість системи дорівнює сумі жорсткостей пружин
Проведемо вісь
звідки отримаємо
Відносно цього положення, яке в подальшому вважаємо початком відліку х – координати,. будуть здійснюватися коливання. Запишемо диференціальне рівняння вільних незгасаючих коливань відносно нового положення рівноваги
або
Кругова частота коливань
Розв’язок диференціального рівняння коливань запишемо в вигляді
що для швидкості точки дає
Підставимо початкові умови в ці вирази та отримаємо рівняння для визначення амплітуди та початкової фази коливань:
Якщо піднести ці вирази до другого ступеня та скласти, то можна отримати вираз для амплітуди, а якщо поділити – то вираз для початкової фази:
З останнього рівняння отримаємо
Підстановка знайдених значень
Тепер початкові умови зараз задовольняються:
і розв’язок рівняння вільних незгасаючих коливань остаточно приймає вигляд
Графік коливань представлений на рис. 5.2. Відповідь: б) Вільні згасаючі коливання з одним ступенем свободи Розглянемо одномірний рух тіла вздовж вісі
тут
в якому:
Коефіцієнт
корені якого мають вигляд
Співвідношення між коефіцієнтом демпфірування
де
визначає кругову частоту коливань. Дійсна частина коренів (5.13) від’ємна, тому загальний розв’язок рівняння (5.9) буде мати вигляд
де
Початкові амплітуда
Коливання, що відбуваються за законом (5.16) називаються згасаючими, бо присутність коефіцієнта
Таким чином, після кожного періоду часу
називається логарифмічним декрементом згасаючих коливань. В випадку
Зауважимо, що явище аперіодичного руху використовується в демпферних пристроях. Контрольні запитання 1. Сформулюйте умови виникнення згасаючих коливань. 2. Запишіть диференціальне рівняння вільних згасаючих коливань. Що необхідно знати для однозначного розв’язку такого рівняння? 3. Як отримати розв’язок такого рівняння? 4. Запишіть розв’язок диференціального рівняння вільних згасаючих коливань. 5. Що таке амплітуда коливань? За яким законом змінюється амплітуда коливань? Що визначає декремент згасання? 6. Від чого залежить період (частота) коливань? Як впливає сили тертя на частоту (період) коливань? 7. Коли виникають аперіодичні коливання? Яке застосування таких процесів Ви знаєте? РОЗДІЛ ІІІ. ДИНАМІКА Динаміка є частиною теоретичної механіки, в якій вивчається рух тіл як результат їх взаємодії. Основи динаміки були закладені Ньютоном, який узагальнив накопичені до нього досліди по руху тіл і сформулював три основні закони механіки, які відомі з курсу фізики. Динаміку розділяють на дві частини: динаміку матеріальної точки, де вивчають рух тіла, розмірами якого можна нехтувати в конкретній задачі та динаміку механічної системи – сукупності матеріальних точок, положення та рух кожної з яких залежить від положення та руху усіх останніх. ЧАСТИНА І. ДИНАМІКА ТОЧКИ Пряма задача динаміки Пряма (перша) задача динаміки – визначити рівнодійну сил 1. Якщо закон руху матеріальної точки задано векторним способом
який еквівалентний трьом скалярним рівнянням:
то задача розв’язується однозначно шляхом подвійного диференціювання рівнянь руху. Дійсно, швидкість визначиться як перша похідна закону руху за часом
Дійсно, визначивши
(тут З останнього рівняння випливає, що сила
Контрольні запитання 1. Сформулюйте перший закон Ньютона. Наведіть приклади. 2. Які системи відліку називаються інерціальними? 3. Сформулюйте принцип відносності Галілея. 4. Яка фізична величина є мірою інертності тіла? 5. Якою фізичною величиною характеризується зміна стану спокою або руху тіла зі сталою швидкістю? 6. Сформулюйте другий закон Ньютона. 7. Сформулюйте третій закон Ньютона. 8. Сформулюйте першу задачу динаміки. Як вона розв’язується коли закон руху матеріальної точки задано векторним (координатним) способом? 9. Як розв’язується перша задача динаміки коли рівняння руху матеріальної точки задано у натуральній формі? Методика розв’язання прямої задачі динаміки 1) Послідовно знаходимо першу та другу похідні закону руху за часом. 2) Використовуємо другий закон Ньютона і знаходимо силу за відомою масою точки.
Тіла масою Розв’язання. До тіла прикладені зовнішня сила Запишемо диференціальне рівняння руху тіла
Введемо декартову систему координат, спрямувавши вісь Спроектуємо попереднє векторне рівняння руху на декартові вісі:
З останнього рівняння знаходимо
що дозволяє визначити силу тертя
і підставляємо у диференціальне рівняння руху (1). Тоді отримуємо з врахуванням (4)
З останнього знаходимо вираз для сили на будь-який момент часу
Підставляючи дані задачі, знаходимо величину сили у момент часу
Відповідь:
|
|||||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 331; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.150.55 (0.216 с.) |
 , що діють на матеріальну точку, якщо відома її маса
, що діють на матеріальну точку, якщо відома її маса  та закон руху.
та закон руху. , (1.1)
, (1.1) ,
,  ,
,  , (1.2)
, (1.2) , а прискорення – як друга похідна
, а прискорення – як друга похідна  . Тоді для визначення сили
. Тоді для визначення сили  . (1.3)
. (1.3) 2. Якщо закон руху матеріальної точки масою
2. Якщо закон руху матеріальної точки масою  , то задача розв’язується однозначно шляхом диференціювання закону руху.
, то задача розв’язується однозначно шляхом диференціювання закону руху. та
та  , можна знайти проекції рівнодійної сили
, можна знайти проекції рівнодійної сили  , головну нормаль
, головну нормаль  та бінормаль
та бінормаль  ) з наступних рівнянь:
) з наступних рівнянь:
 , (1.4)
, (1.4)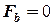 ,
, - радіус кривизни траєкторії).
- радіус кривизни траєкторії). , під дією якої рухається матеріальна точка, лежить в стичній площині, яка дотична до траєкторії точки. Модуль сили
, під дією якої рухається матеріальна точка, лежить в стичній площині, яка дотична до траєкторії точки. Модуль сили  з дотичною до траєкторії руху – рис. 1.1) знаходимо з формул:
з дотичною до траєкторії руху – рис. 1.1) знаходимо з формул: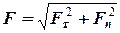 , (1.5)
, (1.5) . (1.6)
. (1.6) в даний момент часу.
в даний момент часу. тієї точки переносника, в якій знаходиться рухоме тіло в даний момент часу, та відповідні складові сил інерції.
тієї точки переносника, в якій знаходиться рухоме тіло в даний момент часу, та відповідні складові сил інерції. ≠ 0 та
≠ 0 та  Приклад 1. Горизонтальна трубка
Приклад 1. Горизонтальна трубка  починає обертатися навколо вертикальної осі (рис. 4.3) за законом
починає обертатися навколо вертикальної осі (рис. 4.3) за законом  (рад). Одночасно механізм М масою
(рад). Одночасно механізм М масою  = 0,2 кг починає рух вздовж трубки за законом відносного руху
= 0,2 кг починає рух вздовж трубки за законом відносного руху  = ОМ =
= ОМ = 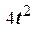 (см). Вважаючи механізм матеріальною точкою, визначити сили інерції, які діють на нього на момент часу
(см). Вважаючи механізм матеріальною точкою, визначити сили інерції, які діють на нього на момент часу  = 2 c та зобразити їх на рисунку. Записати рівняння відносного руху матеріальної точки М.
= 2 c та зобразити їх на рисунку. Записати рівняння відносного руху матеріальної точки М. , (1)
, (1) в неінерціальній системі, зумовлені як обертальним рухом трубки, так і відносним рухом точки по ньому. Таким чином, при визначенні сил інерції спочатку враховуємо дві складові, які пов’язані з обертанням трубки
в неінерціальній системі, зумовлені як обертальним рухом трубки, так і відносним рухом точки по ньому. Таким чином, при визначенні сил інерції спочатку враховуємо дві складові, які пов’язані з обертанням трубки , (2)
, (2)
 . (3)
. (3) . (4)
. (4) ), його відносну швидкість
), його відносну швидкість  , кутову швидкість
, кутову швидкість  обертання трубки
обертання трубки  = ОМ = 4·22 = 16 см.
= ОМ = 4·22 = 16 см.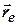 відносного положення механізму М спрямований вздовж трубки та має модуль 16 см (рис. 4.4 а – вид на горизонтальну площину, рис. 4.4 б - вид на фронтальну площину).
відносного положення механізму М спрямований вздовж трубки та має модуль 16 см (рис. 4.4 а – вид на горизонтальну площину, рис. 4.4 б - вид на фронтальну площину). Знайдемо відносну швидкість механізму М як першу похідну від рівняння відносного руху за часом
Знайдемо відносну швидкість механізму М як першу похідну від рівняння відносного руху за часом =
= 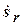 =
=  .
. знайдемо як першу похідну кута повороту диска за часом
знайдемо як першу похідну кута повороту диска за часом =
= 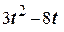 ,
,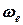 = 3·22 – 8·2 = – 4 рад/с.
= 3·22 – 8·2 = – 4 рад/с. =
= 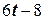 ,
,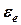 = 4 рад/с2.
= 4 рад/с2. ,
, 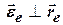 , та
, та  , послідовно знайдемо модуль обертальної сили інерції
, послідовно знайдемо модуль обертальної сили інерції = 0,2·4·0,16 = 0,128 Н, (5)
= 0,2·4·0,16 = 0,128 Н, (5) = 0,2·42·0,16 = 0,512 Н, (6)
= 0,2·42·0,16 = 0,512 Н, (6) = 2·0,2·4·0,16·1 = 0,256 Н. (7)
= 2·0,2·4·0,16·1 = 0,256 Н. (7) (рис. 4.5) набуває вигляду
(рис. 4.5) набуває вигляду .
. Розв’язуємо дане диференціальне рівняння де кутова швидкість стала і дорівнює
Розв’язуємо дане диференціальне рівняння де кутова швидкість стала і дорівнює 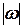 = 4 рад/с з початковими умовами для нового початку відліку часу (t = 0 c):
= 4 рад/с з початковими умовами для нового початку відліку часу (t = 0 c):  = 16 см та
= 16 см та  = 16 см/с.
= 16 см/с. = 0.
= 0. , тому загальний розв’язок рівняння буде мати вигляд
, тому загальний розв’язок рівняння буде мати вигляд .
. та
та  знаходимо з початкових умов: спочатку визначимо швидкість точки
знаходимо з початкових умов: спочатку визначимо швидкість точки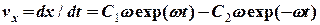 ,
, ,
, ,
, ,
,  ,
, = 0,1 м,
= 0,1 м,  = 0,06 м.
= 0,06 м. м.
м.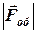 = 0,128 Н,
= 0,128 Н,  = 0,512 Н,
= 0,512 Н, 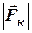 = 0,256 Н; після цього (з новим відліком часу) точка рухається за законом
= 0,256 Н; після цього (з новим відліком часу) точка рухається за законом  називаються вільними (власними) незгасаючими. Такі одномірні коливання, наприклад, вздовж осі
називаються вільними (власними) незгасаючими. Такі одномірні коливання, наприклад, вздовж осі 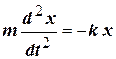 ,
, = 0:
= 0:  та
та  , чи
, чи = 0, (5.1)
= 0, (5.1) – кругова частота коливань,
– кругова частота коливань,  – коефіцієнт жорсткості пружини, а відлік осі
– коефіцієнт жорсткості пружини, а відлік осі  = 0. (5.2)
= 0. (5.2) ,
,  ), тому загальний розв’язок рівняння (5.1) набуває вигляду
), тому загальний розв’язок рівняння (5.1) набуває вигляду ,
, та
та  – сталі інтегрування.
– сталі інтегрування. , (5.3)
, (5.3) та
та  визначаються з початкових умов як:
визначаються з початкових умов як: ,
,  .
. . (5.4)
. (5.4) вказує найбільше відхилення точки від положення рівноваги і називається амплітудою коливань, величина
вказує найбільше відхилення точки від положення рівноваги і називається амплітудою коливань, величина  – фазою коливань, а
– фазою коливань, а  – початковою фазою коливань.
– початковою фазою коливань. , (5.5)
, (5.5) . (5.6)
. (5.6) , (
, ( = 0; 1), (5.7)
= 0; 1), (5.7) = 60Н/м та
= 60Н/м та  = 140 Н/м (рис. 5.1) і знаходиться на похилій площині під кутом 45º до горизонту. Точка закріплення тіла ділить відстань між пружинами у відношенні обернено пропорційно жорсткостям пружин. Знайти: 1) положення рівноваги, відносно якого мають місце коливання; 2) записати диференціальне рівняння вільних незгасаючих коливань та розв’язати його для початкових умов
= 140 Н/м (рис. 5.1) і знаходиться на похилій площині під кутом 45º до горизонту. Точка закріплення тіла ділить відстань між пружинами у відношенні обернено пропорційно жорсткостям пружин. Знайти: 1) положення рівноваги, відносно якого мають місце коливання; 2) записати диференціальне рівняння вільних незгасаючих коливань та розв’язати його для початкових умов  = 0,1 м,
= 0,1 м,  = – 2,0 м/с; 3) визначити частоту
= – 2,0 м/с; 3) визначити частоту  , початкову фазу
, початкову фазу  Розв’язання. Перш за все, знайдемо ефективний коефіцієнт жорсткості
Розв’язання. Перш за все, знайдемо ефективний коефіцієнт жорсткості  , а сумарна сила розтягу двох пружин є сумою сил деформації кожної пружини
, а сумарна сила розтягу двох пружин є сумою сил деформації кожної пружини ,
, = 200 Н/м.
= 200 Н/м. вздовж похилої площини з початком у точці закріплення тіла (рис. 5.1). Положення рівноваги
вздовж похилої площини з початком у точці закріплення тіла (рис. 5.1). Положення рівноваги  визначимо з умови рівності сили пружності
визначимо з умови рівності сили пружності  і проекції сили тяжіння на похилу площину
і проекції сили тяжіння на похилу площину  45º, тобто з рівняння
45º, тобто з рівняння 45º,
45º, .
. визначається жорсткістю системи пружин та масою тіла, і в нашому прикладі
визначається жорсткістю системи пружин та масою тіла, і в нашому прикладі = 20 рад/с.
= 20 рад/с. =
=  , (2)
, (2) . (3)
. (3) ,
,  . (4)
. (4) =
=  = 0,14 м, (5)
= 0,14 м, (5) = 0,1·20/(– 2,0) = –1.
= 0,1·20/(– 2,0) = –1. (–1) = –
(–1) = –  рад. (6)
рад. (6) = 0,14 і
= 0,14 і 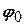 = –
= –  . Тому, з урахуванням властивостей тангенса, треба додати до знайденого значення початкової фази
. Тому, з урахуванням властивостей тангенса, треба додати до знайденого значення початкової фази  - період тангенса. Тоді
- період тангенса. Тоді = 2,356 рад.
= 2,356 рад.
 = 0,1 м =
= 0,1 м =  = –2,0 м/с =
= –2,0 м/с =  м.
м. = 0,018 м,
= 0,018 м,  = 20 рад/с,
= 20 рад/с,  рад,
рад,  м.
м. , (5.8)
, (5.8) , (5.9)
, (5.9) ,
,  . (5.10)
. (5.10) називається відносним коефіцієнтом демпферування коливань. Зауважимо, що розмірності
називається відносним коефіцієнтом демпферування коливань. Зауважимо, що розмірності  , (5.11)
, (5.11) . (5.12)
. (5.12) , (5.13)
, (5.13) , (5.14)
, (5.14) , (5.15)
, (5.15) . (5.16)
. (5.16) та фаза
та фаза  визначаються початковими умовами і ми знаходимо їх аналогічно тому, як для вільних коливань:
визначаються початковими умовами і ми знаходимо їх аналогічно тому, як для вільних коливань: , (5.17)
, (5.17) ,
,  при амплітуді коливань зумовлює поступове зменшення максимального відхилення тіла від положення рівноваги з плином часу і до зникнення коливань. Отже рух точки можна розглядати як гармонічне коливання з круговою частотою
при амплітуді коливань зумовлює поступове зменшення максимального відхилення тіла від положення рівноваги з плином часу і до зникнення коливань. Отже рух точки можна розглядати як гармонічне коливання з круговою частотою  та амплітудою
та амплітудою  , яка змінюється за законом
, яка змінюється за законом . (5.19)
. (5.19) , послідовні відхилення від положення рівноваги створюють геометричну прогресію зі знаменником
, послідовні відхилення від положення рівноваги створюють геометричну прогресію зі знаменником  , який називається декрементом згасання, а величина
, який називається декрементом згасання, а величина
 (5.20)
(5.20)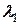 та
та  будуть дійсними та від’ємними, а точка буде здійснювати аперіодичний згасаючий рух за законом
будуть дійсними та від’ємними, а точка буде здійснювати аперіодичний згасаючий рух за законом , (5.21)
, (5.21)
 при
при 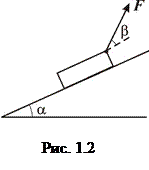 Приклад 1. Визначення сили, коли заданий закон руху матеріальної точки.
Приклад 1. Визначення сили, коли заданий закон руху матеріальної точки. 1 кг піднімається по похилій площині (рис. 1.2) під дією сили
1 кг піднімається по похилій площині (рис. 1.2) під дією сили  (м). Знайти вираз для сили, яка забезпечує рух, якщо
(м). Знайти вираз для сили, яка забезпечує рух, якщо  = 0,2. Визначити значення сили у момент часу
= 0,2. Визначити значення сили у момент часу 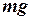 , сила тертя
, сила тертя  та нормальна реакція
та нормальна реакція  (рис. 1.3). Нормальна реакція
(рис. 1.3). Нормальна реакція  .
. – перпендикулярно до неї.
– перпендикулярно до неї. , (1)
, (1) . (2)
. (2) , (3)
, (3) . (4)
. (4) Знаходимо послідовно першу та другу похідну від закону руху
Знаходимо послідовно першу та другу похідну від закону руху ,
, 

 .
. . (5)
. (5) = 2 с.
= 2 с. Н.
Н.


