
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теория устойчивости гидрофобных дисперсных систем ДЛФОСодержание книги
Поиск на нашем сайте
Современная физическая теория коагуляции электролитами основана на общих принципах статистической физики, теории молекулярных сил и теории растворов. Ее авторами являются: Б.В. Дерягин, Л.Д. Ландау (1937-1941), Э. Фервей, Я. Овербек (по первым буквам ДЛФО). Суть теории: между любыми частицами при их сближении возникает расклинивающее давление разделяющей жидкой прослойки в результате действия сил притяжения и отталкивания. Расклинивающее давление является суммарным параметром, учитывающим действие как сил притяжения, так и сил отталкивания. Состояние системы зависит от баланса энергии притяжения (Uпр) и энергии отталкивания (Uотт). Преобладает Uотт – устойчивая система. Преобладает Uпр - нарушение агрегативной устойчивости – коагуляция. Изменение энергии взаимодействия между двумя частицами при их сближении изображают графически (рис. 5.3). Суммарную энергию системы из двух частиц (кривая 3) получают сложением Uотт и Uпр: U=Uотт+Uпр = где: В – множитель, зависящий от значений электрических потенциалов ДЭС, свойств среды, температуры; е – основание натурального логарифма; c – величина, обратная толщине диффузного слоя; h – расстояние между частицами; А – константа молекулярных сил притяжения.
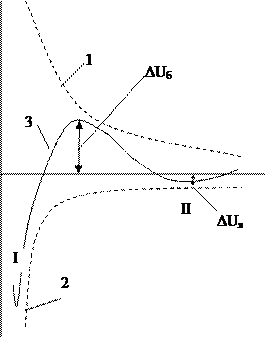
Рис.5.3. Потенциальные кривые взаимодействия коллоидных частиц: 1 – изменение энергии отталкивания с расстоянием; 2 – изменение энергии притяжения; 3 – результирующая кривая.
Рассмотрим результирующую кривую 3 на рис.5.3. На ней имеются характерные участки: - В области малых расстояний имеется глубокий первичный минимум (потенциальная яма) – значительно преобладает Uпр. Первичный минимум отвечает непосредственному слипанию частиц (I). - В области больших расстояний - вторичный неглубокий минимум (вторая потенциальная яма, отвечает притяжению через прослойку среды). На схеме II. - В области средних расстояний на кривой имеется максимум и, если он расположен над осью абсцисс, то появляется энергетический барьер сил отталкивания (DUб).
Результирующая кривая 3 может иметь различный вид в зависимости от устойчивости дисперсной системы (рис.5.4.).
Рис. 5.4. Потенциальные кривые для определенных состояний устойчивости дисперсной системы: 1 - в системе при любом расстоянии между частицами преобладает энергия притяжения над энергией отталкивания. В такой системе наблюдается быстрая коагуляция с образованием агрегатов. 2 - достаточно высокий потенциальный барьер и наличие вторичного минимума. Частицы взаимодействуют, но не имеют непосредственного контакта и разделены прослойками среды. 3 - система с высокой агрегатной устойчивостью (высокий потенциальный барьер и отсутствие вторичного минимума или при его глубине, меньшей тепловой энергии kТ).
В зависимости от высоты энергетического барьера и глубины потенциальных ям возможны различные варианты поведения частиц при сближении (рис.5.5), частицы обладают кинетической энергией – kТ.
Рис.5.5. Схемы взаимодействия коллоидных частиц
Дисперсная система агрегативно устойчива при высоком энергетическом барьере сил отталкивания. Скорость коагуляции
Рис.5.6. Зависимость скорости коагуляции от Концентрации электролита
В области медленной коагуляции скорость сильно зависит от концентрации (отрезок АВ). В точке В скорость становиться постоянной и не зависит от концентрации электролита – здесь значение z - потенциала равно нулю – начало быстрой коагуляции. Концентрацию электролита, начиная с которой скорость коагуляции остается постоянной, называют порогом быстрой коагуляции. Теории кинетики коагуляции разработаны Смолуховским (1916г). Рассматривают коагуляцию как реакцию второго порядка, в элементарном акте которой участвуют две частицы: Уравнение Смолуховского для расчета числа частиц, слипшихся по m-штук за время t:
При быстрой коагуляции все столкнувшиеся частицы реагируют (DUб=0). Уравнение Смолуховского для константы скорости быстрой коагуляции:
где h- вязкость среды.
При медленной коагуляции не все столкновения приводят к слипанию. Уравнение Смолуховского для медленной коагуляции:
где Р – стерический множитель, учитывающий благоприятные пространственные расположения частиц при столкновении, их физические размеры. При быстрой коагуляции все столкновения эффективны и Р=1, при медленной Р<1. DЕ – потенциальный барьер, при быстрой коагуляции DЕ=0, при медленной DЕ¹0. h - вязкость. Порог коагуляции можно вычислить из соотношения, теоретически найденного Дерягиным и Ландау и названным законом 6-й степени: энергетический барьер между коллоидными частицами исчезает при достижении критической концентрации (g), которая обратно пропорциональна шестой степени заряда иона-коагулятора:
С – константа, зависящая от числа зарядов катиона и аниона; e - диэлектрическая проницаемость раствора; А – константа Ван –дер –Ваальсового притяжения; е- заряд электрона; k – константа Больцмана; z– зарядность коагулирующего иона.
В соответствии с этим уравнением значения g для элементов с зарядами противоионов 1, 2 и 3 соотносятся как 1:1/26:1/36=1:1/64:1/729. Уравнение хорошо обосновывает эмпирическое правило Шульце-Гарди. В тех случаях, когда велика роль адсорбционно-сольватного фактора устойчивости, проявляется приближенность теории ДЛФО, т.к. она не учитывает роли специфической адсорбции и сродства иона к растворителю. Связь эффективности соударений с потенциальным барьером при коагуляции была показана Фуксом Н.А. Если DЕ значительно больше кТ, то скорость коагуляции может приблизиться к нулю и система окажется агрегативно неустойчивой. В теории, развитой Фуксом, используется представление о коэффициенте замедления коагуляции W, который показывает, во сколько раз константа скорости медленной коагуляции меньше константы скорости быстрой коагуляции. Учитывая выражения для Кб и Км, получим:
Коэффициент W называют фактором устойчивости или коэффициентом стабильности.
Старение золей Лиофобные коллоиды обладают слабым взаимодействием дисперсной фазы и дисперсионной среды и характеризуются склонностью к уменьшению дисперсности со временем. Избыток свободной поверхностной энергии, полученной частицами при их образовании, является (согласно второму началу термодинамики) основной причиной перехода в более устойчивое состояние, которое определяется укрупнением частиц. Самопроизвольный процесс укрупнения частиц (уменьшения степени дисперсности) в лиофобных золях, называется старением или автокоагуляцией. Скорость старения гораздо медленнее, чем коагуляция под воздействием электролитов.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 371; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.235.195 (0.009 с.) |




 Ход коагуляции в зависимости от концентрации коагулирующего электролита можно подразделить на две стадии: медленную и быструю.
Ход коагуляции в зависимости от концентрации коагулирующего электролита можно подразделить на две стадии: медленную и быструю.

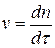 .
.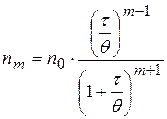 ;
;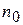 - первоначальное число частиц;
- первоначальное число частиц;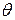 - время половинной коагуляции (
- время половинной коагуляции (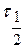 ).
).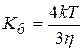 ;
;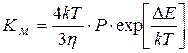 ;
; ;
;



