
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
и структура полимерных гелейСодержание книги
Поиск на нашем сайте
Процесс гелеобразования условно делят на две стадии. Первая стадия характеризуется значительным увеличением вязкости системы, но в целом система сохраняет свойства, присущие растворам. Вторая стадия начинается с момента появления упругости, т.е. начала проявления свойств твердого тела. В дальнейшем, упругость системы возрастает и достигает предельного значения, определяемого условиями гелеобразования. С этой точки зрения механизм гелеобразования можно представить как процесс постепенного возникновения в растворе вторичных образований макромолекул и последующего их взаимодействия, с формированием сплошной пространственной структуры. Переход от раствора к гелю можно рассматривать по аналогии с процессами образования пространственных структур при поликонденсации или процессами сшивания линейных молекул, однако, только качественно. Доказательством двухстадийности процесса гелеобразования является наличие на термографических кривых двух максимумов при застудневании, что объяснено образованием сначала более слабых, а затем более прочных связей, ответственных за образование геля. Существование двух типов связей, различающихся по прочности, типично для студней. Оно истолковывается как образование на начальных стадиях гелеобразования областей гетерогенности из упорядоченных макромолекул. Иными словами, образование структуры в виде устойчивых роев молекул или агрегатов. Их существование подтверждается исследованием методом спектра мутности растворов. Даже при больших разбавлениях растворов, существуют агрегаты молекул, которые не разрушаются даже при слабой термической обработке растворов или их сильном разбавлении. Вторая стадия заключается в связывании агрегатов друг с другом и образование сетки. Основной вопрос при изучении структуры гелей – вопрос о межмолекулярных связях. Он подробно обсуждался в литературе на примере желатины, поскольку она имеет сложное химическое строение. В желатине возможно образование связей различных типов: электростатических, неполярных, полярных, водородных. На основе установления сильного влияния на температуру плавления геля желатины добавок мочевины и ацетамида и слабого влияния неполярных добавок был сделан вывод о том, что взаимодействие в желатине обусловлено главным образом полярными группами. Существует и противоположное мнение, в соответствии с которым, гели желатины формируются в результате образования связей между неполярными группами, так как полярные группы взаимодействуют с водой. Однако, появление связей между молекулами полимера в полярном растворителе может иметь место, если энергия связи полимер-полимер больше энергии связи полимер-растворитель. Химическая природа желатины допускает разные виды связей в геле, в том числе и за счет полярных групп. Ряд исследователей полагает, что при гелеобразовании узлами сетки являются не локальные связи, а упорядоченные участки цепей, объединенные водородными связями. Таким образом, на основании рассмотрения существующих представлений о механизме гелеобразования в растворах полимеров, можно сделать вывод, что процесс заключается в образовании прочных межмолекулярных связей как локализованного, так и нелокализованного типов. При этом в формировании пространственной сетки существенную роль играет взаимодействие не отдельных цепей, а агрегатов молекул. Существуют попытки рассмотреть механизм гелеобразования в рамках механизма зародышеобразования, т.е. в рамках классической термодинамики. Однако схема структуры студня, сформировавшегося по механизму зародышеобразования при фазовом распаде, применима только к неравновесным студням, которые можно получить только одним путем. Однако гель может быть получен как при застудневании, так и при ограниченном набухании, т.е. состояние геля может быть достигнуто с двух разных сторон, что не объясняет схема строения, предложенная в рамках механизма зародышеобразования. Более подходящей термодинамической основой для описания образования студней при фазовом переходе является теория спинодального распада.
Реология гелей Реология – наука о течении и деформации материала. Первоначально под термином реология подразумевалась классическая механика и эластичность потоков ньютоновских жидкостей, типа воды и малых деформаций твердых тел, типа стали и древесины. Сейчас, практически, слово «реология» относят к течению и деформации «неклассических» материалов: резины, пластмасс, растворов полимеров, расплавов стекла, почвы и т.д. Для изучения реологических характеристик гелей используют следующие параметры:
Между этими параметрами существует определенная взаимосвязь:
Эта формула является выражением закона Ньютона или закона течения идеальных вязких жидкостей. На рис. 9.1 приведена схема, иллюстрирующая сдвиговое течение жидкости в ламинарном режиме.
Рис. 9.1. Схема сдвигового течения жидкости.
На основе этой схемы можно получить выражение для скорости сдвига На рисунке приняты следующие обозначения: х - расстояние между соседними движущимися слоями; l- линейное смещение отдельного слоя за время t;
Из схемы следует, что градиент скорости Для идеальных жидкостей градиент скорости прямопропорционален напряжению сдвига:
Здесь Поскольку
Вязкость ньютоновских жидкостей постоянна, т.е. она не зависит от характеристик потока. Для неньютоновских сред вязкость зависит от параметров течения, т.е. существуют зависимости:
Эти зависимости принято называть реологическими кривыми или кривыми течения. По форме реологические кривые неньютоновских систем делят на три группы: - бингамовские (вязкопластичные среды); - псевдопластичные; - дилатантные.
Ниже на рис. 9.2 приведены кривые течения различных тел:
Рис. 9.2. Кривые течения различных тел: 1- ньютоновская жидкость; 2 – идеальнопластичное тело (тело Бингама – деформация по закону Ньютона после достижения некоторого предела сдвига 3 – псевдопластическая система; 4 – дилатантная жидкость.
Реологические кривые перечисленных систем в первом приближении описываются следующими уравнениями: ньютоновские среды – бингамовские среды – псевдопластические среды – дилатантные среды – Вязкость псевдопластичных сред с ростом скорости сдвига уменьшается (тиксотропия), дилатантных сред, напротив, возрастает (реолексия). Механизм явлений, который приводит к аномальному поведению жидкостей не всегда ясен. Поэтому для описания закономерностей деформации жидких систем применяют механические модели, составленные из простых механических элементов. Для приготовления печатных красок используются системы, которые характеризуются псевдопластическим характером течения. Полные реологические кривые таких систем имеют вид, показанный на рис. 9.3:
Рис. 9.3. Полные реологические кривые псевдопластических сред.
Выбор логарифмических координат обусловлен тем, что в таком представлении наиболее важный участок (с наиболее интенсивным падением вязкости) имеет линейную форму. Освальд-де-Вилл предложил для его описания уравнение степенного вида:
где
Уравнением широко пользуются, так как оно позволяет графическим способом определить его коэффициенты. Коэффициент
Реологические теории. Существует достаточно большое количество различных реологических теорий. Все теории можно условно разбить на 4 группы: - теории Эйринга и его последователей; - структурные теории; - гидродинамические теории; - другие (например те, которые частично относятся к каждой из перечисленных).
Теория Эйринга Теория Г. Эйринга связывает явление аномальной вязкости с влиянием Эйринг представлял вязкую среду как совокупность молекулярно-кинетических единиц (МКЕ). МКЕ не имеют определенной формы и способны перемещаться в пространстве: перескакивать с места на место с определенной частотой. При этом МКЕ преодолевают потенциальный барьер. По теории абсолютных скоростей, частота перескока пропорциональна экспоненте высоты потенциального барьера:
где
Если вероятность перехода МКЕ через энергетический барьер во всех направлениях одинакова, направление течения отсутствует. Воздействие на систему внешней силы эквивалентно снижению склонов потенциального барьера в направлении его и увеличению в направлении от него (кривая пунктиром на рис. 9.4).
Рис. 9.4. Снижение потенциального барьера при воздействии на систему внешней силы. На основе своих предположений Эйринг предложил следующую зависимость:
где
Уравнением Эйринга, однако, нельзя описать реальные реологические кривые. Недостатком этого уравнения является отсутствие наименьшего значения вязкости
Структурные теории. Структурные теории вязкости рассматривают зависимость вязкости от режимов течения как процесс обратимого разрушения – восстановления надмолекулярной структуры полимера. Разрушение и восстановление связывают с множеством различных процессов, происходящих при течении: перемещением слоев потока, вращением клубков макромолекул, разрушением и образованием новых межмолекулярных связей. Структурные теории не имеют своих реологических уравнений. В них используются математические модели, основанные на теории Эйринга. В структурных теориях определяют степень разрушения структуры
где
Структурные теории позволяют объяснить ряд явлений, которые пока нельзя описать на основе других теорий, например, явление сдвигового повышения вязкости под влиянием напряжения сдвига (образование дополнительных связей под влиянием напряжения сдвига, ориентация движения макромолекул вдоль потока, благоприятное пространственное расположение макромолекул для формирования дополнительных связей).
Гидродинамические теории Гидродинамические теории объясняют снижение вязкости изменением формы и соответственно сопротивления перемещению молекул в среде. Гидродинамические теории рассматривают поведение каждой молекулы как независящее от остальных. Основной гидродинамический эффект обусловлен трением между частицей и средой (растворителем). Интенсивность этого трения является пропорциональной скорости перемещения суспендированной частицы в жидкости. При деформации суспензий происходит ориентация частиц в потоке. Это изменяет условие обтекания частиц средой и вязкость системы. Теория Грессли Грессли предложил для описания реологических свойств высокомолекулярных сред концепцию строения полимерных систем. Согласно этой концепции, высокомолекулярные системы имеют сетчатую структуру. Узлы сетки возникают в результате контакта длинных гибких макромолекул, но природа узлов при этом не рассматривается. Грессли предположил, что вязкость пропорциональна плотности узлов в среде. Для практического использования предложил полуэмпирическую модель:
Это уравнение широко используется на практике. Используется также уравнение Кросса:
Эти уравнения удовлетворительно описывают изменение вязкости гелей с ростом напряжения сдвига и применяются для описания реологического поведения загусток и печатных красок в химической технологии. СОДЕРЖАНИЕ
|
||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 264; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.218.231.116 (0.008 с.) |

 - напряжение сдвига, Па, гПа,
- напряжение сдвига, Па, гПа,  ;
; - скорость сдвига (производная функции по времени), 1/с,
- скорость сдвига (производная функции по времени), 1/с,  ;
;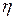 - вязкость, Па.с.
- вязкость, Па.с.

 - скорость смещения слоя;
- скорость смещения слоя; - деформация сдвига;
- деформация сдвига; равен скорости деформации:
равен скорости деформации: 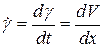 .
.
 , можно записать:
, можно записать:

 ). Тела, имеющие определенную величину предела текучести, называются пластичными, а их деформации – пластическими;
). Тела, имеющие определенную величину предела текучести, называются пластичными, а их деформации – пластическими;
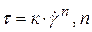 <1®
<1®  >0
>0

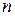 - индекс течения.
- индекс течения. , а
, а  равен расстоянию от начала координат до пересечения прямой, продлевающей реологическую кривую до ее пересечения с осью
равен расстоянию от начала координат до пересечения прямой, продлевающей реологическую кривую до ее пересечения с осью 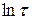 .
. на высоту потенциального барьера, препятствующего переходу молекулярно-кинетических единиц из одного равновесного положения в другое.
на высоту потенциального барьера, препятствующего переходу молекулярно-кинетических единиц из одного равновесного положения в другое.
 - частота перескоков в свободном состоянии;
- частота перескоков в свободном состоянии;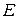 - высота потенциального барьера;
- высота потенциального барьера; - абсолютная температура;
- абсолютная температура;

 - знак гиперболического синуса.
- знак гиперболического синуса. , которое соответствует предельному разрушению структуры.
, которое соответствует предельному разрушению структуры. , или восстановления
, или восстановления  :
: ,
,  ,
, – наибольшая ньютоновская вязкость;
– наибольшая ньютоновская вязкость; - наименьшая ньютоновская вязкость.
- наименьшая ньютоновская вязкость.




