
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Краевые задачи для эллиптических уравнений.
Рассмотрим ограниченную связную область
Задача Дирихле( первая краевая задача ) Требуется найти функцию Внутренняя задача Дирихле. Теорема 1. Если решение Доказательство. Пусть существуют два решения Так как функция Теорема 2. Решение задачи Дирихле (4), (5), в предположении его существования в пространстве Теорема Шаудера. Пусть в уравнении (1) коэффициенты
Из приведённых теорем следует, что в пространствах Рассмотрим область Внешняя задача Дирихле в Требуется найти функцию Задача Неймана для уравнения Пуассона. Рассмотрим ограниченную область
Внутренняя задача Неймана( вторая краевая задача ). Теорема 3. Пусть функция Доказательство. Воспользуемся первой формулой Грина, рассмотрев в качестве функции Учитывая равенства (10), (11), получаем соотношение (12). ■ Теорема 4. Если существует решение Внешняя задача Неймана в Теорема5. Если существует решение
|
|||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 248; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.144.6 (0.006 с.) |
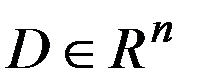 с граничной поверхностью
с граничной поверхностью 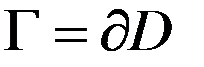 , охватывающей область
, охватывающей область 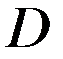 . Пусть
. Пусть 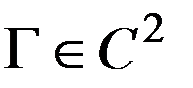 . В области
. В области 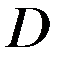 зададим эллиптическое уравнение 2 порядка с достаточно гладкими коэффициентами:
зададим эллиптическое уравнение 2 порядка с достаточно гладкими коэффициентами: 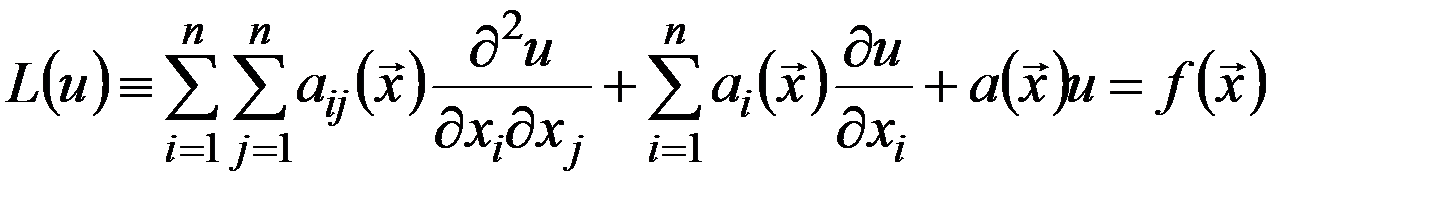 , (1) где
, (1) где 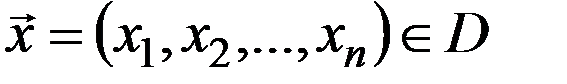 .Пусть искомая функция
.Пусть искомая функция 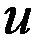 на границе
на границе 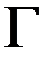 принимает заданные значения, то есть
принимает заданные значения, то есть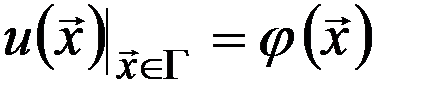 ,где
,где 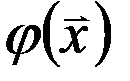 - заданная функция на поверхности
- заданная функция на поверхности 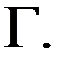
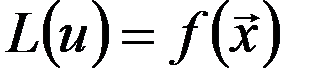 в области
в области 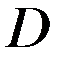 , (2)
, (2) 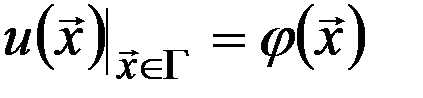 ,(3) где
,(3) где 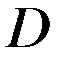 – ограниченная область.
– ограниченная область.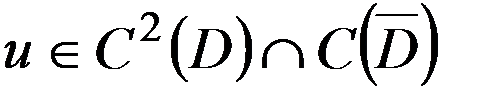 , которая удовлетворяет уравнению (2) в области
, которая удовлетворяет уравнению (2) в области 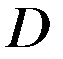 и граничному условию (3) на граничной поверхности
и граничному условию (3) на граничной поверхности 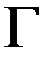 .
.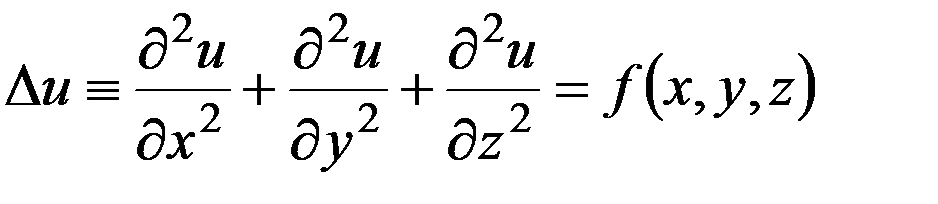 вобласти
вобласти 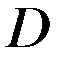 , (4)
, (4) 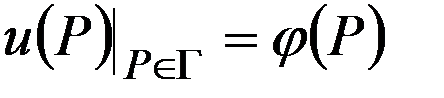 , (5) где
, (5) где 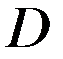 – ограниченная область. Решение
– ограниченная область. Решение 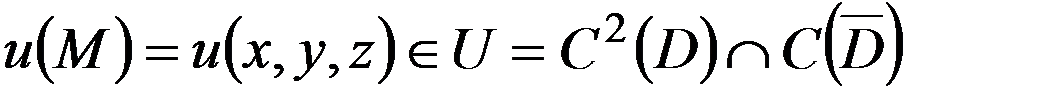 называется классическим решением задачи (4.19), (4.20). ■
называется классическим решением задачи (4.19), (4.20). ■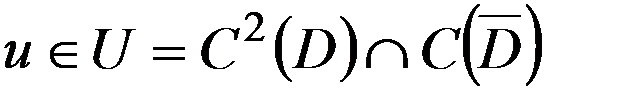 задачи Дирихле (4), (5) существует, тогда оно единственно в пространстве
задачи Дирихле (4), (5) существует, тогда оно единственно в пространстве 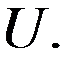
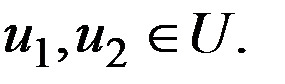 Образуем функцию
Образуем функцию 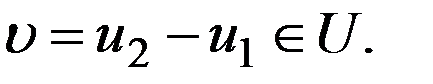 Очевидно, что выполнены условия:
Очевидно, что выполнены условия: 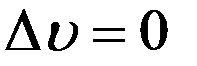 в области
в области 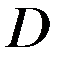 ,
, 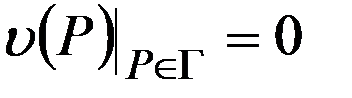 . (6)
. (6)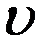 гармоническая в области
гармоническая в области 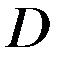 , то для нее выполнен принцип максимума и минимума. Учитывая (6), получаем
, то для нее выполнен принцип максимума и минимума. Учитывая (6), получаем  ,
, 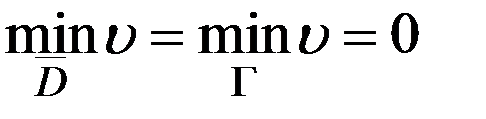 . Следует
. Следует 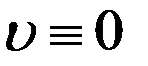 в
в 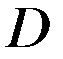 , значит
, значит 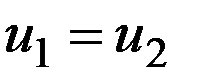 ■
■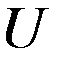 , непрерывно зависит от граничных функций
, непрерывно зависит от граничных функций 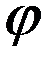 .
.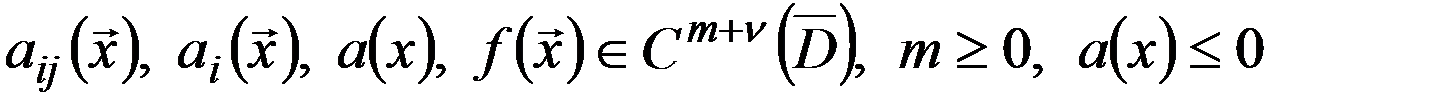 , граничная поверхность
, граничная поверхность 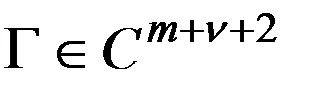 , граничная функция
, граничная функция 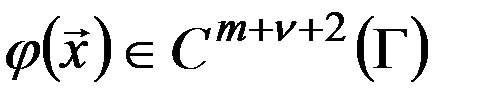 . Пусть выполнено неравенство (2):
. Пусть выполнено неравенство (2):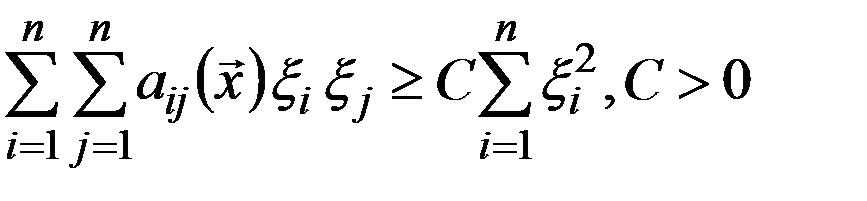 , тогда существует единственное решение задачи (1), (2)
, тогда существует единственное решение задачи (1), (2) 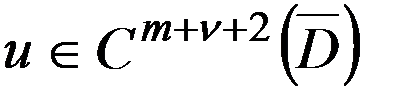 . ■
. ■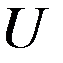 и
и 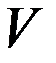 задача Дирихле (1), (2) для уравнения Пуассона поставлена корректно.
задача Дирихле (1), (2) для уравнения Пуассона поставлена корректно.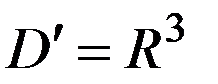 \
\ 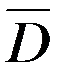 , внешнюю по отношению к ограниченной области
, внешнюю по отношению к ограниченной области 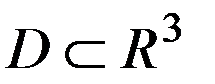 . Для бесконечной области
. Для бесконечной области 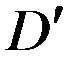 поставим задачу Дирихле для уравнения Пуассона. Наложим условие
поставим задачу Дирихле для уравнения Пуассона. Наложим условие 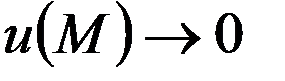 при
при 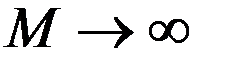 .
.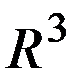 .
. 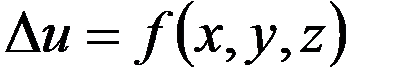 в области
в области 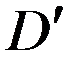 , (7)
, (7) 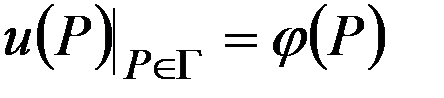 ,(8)
,(8) 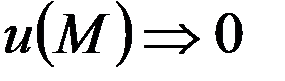 при
при 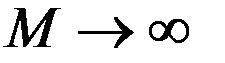 (9)
(9)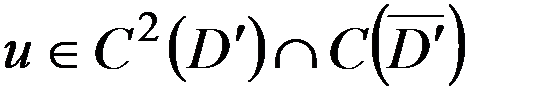 , удовлетворяющую уравнению (7) в области
, удовлетворяющую уравнению (7) в области  , граничному условию (8) и равномерно стремится к нулю на бесконечности. Если опустить условие на бесконечности (9), тогда задача может иметь неединственное решение. Для внешней задачи Дирихле на плоскости
, граничному условию (8) и равномерно стремится к нулю на бесконечности. Если опустить условие на бесконечности (9), тогда задача может иметь неединственное решение. Для внешней задачи Дирихле на плоскости 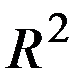 условие (9) необходимо заменить на условие ограниченности решения
условие (9) необходимо заменить на условие ограниченности решения 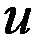 в области
в области 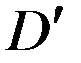 .
.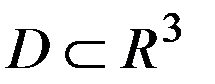 с границей
с границей 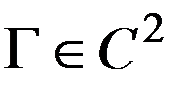 . Для области
. Для области 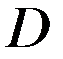 поставим краевую задачу для уравнения Пуассона, когда на поверхности
поставим краевую задачу для уравнения Пуассона, когда на поверхности 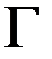 задана производная функции
задана производная функции 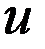 .
.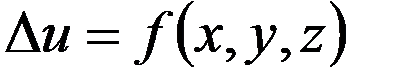 в
в 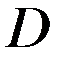 ,
, 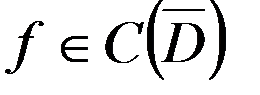 ,(10)
,(10) 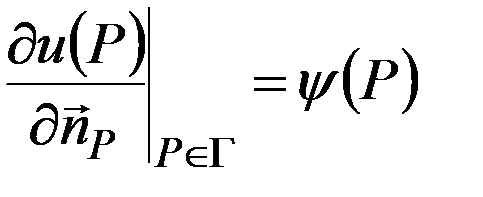 ,
, 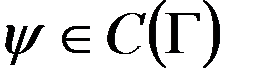 ,(11) где
,(11) где 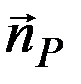 - внешняя единичная нормаль к поверхности
- внешняя единичная нормаль к поверхности 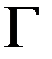 в точке
в точке 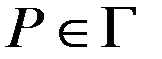 .Требуется найти функцию
.Требуется найти функцию 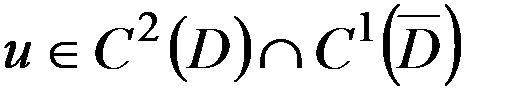 , которая удовлетворяет уравнению (10) в области
, которая удовлетворяет уравнению (10) в области 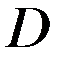 и граничному условию (11) на граничной поверхности
и граничному условию (11) на граничной поверхности 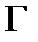 области
области 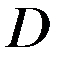 .
.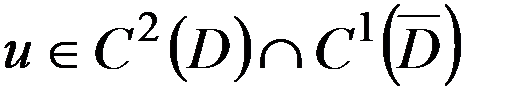 является решением задачи (10), (11), тогда
является решением задачи (10), (11), тогда 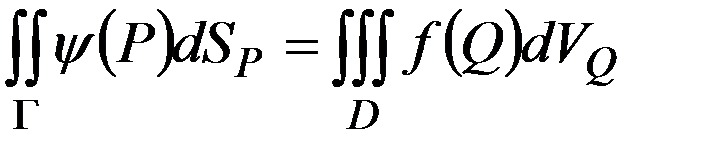 , (12)- является необходимым условием разрешимости задачи Неймана (10), (11).
, (12)- является необходимым условием разрешимости задачи Неймана (10), (11).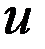 решение задачи (10), (11) и положив
решение задачи (10), (11) и положив 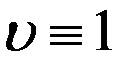 . В результате
. В результате 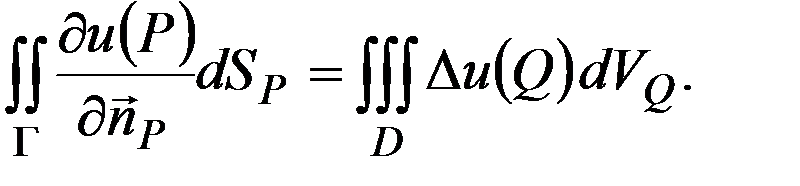
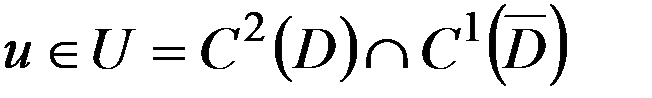 внутренней задачи Неймана (10), (11), тогда оно единственно с точностью до постоянного слагаемого.
внутренней задачи Неймана (10), (11), тогда оно единственно с точностью до постоянного слагаемого.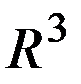 .
. 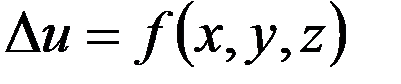 в области
в области 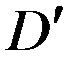 , (14)
, (14) 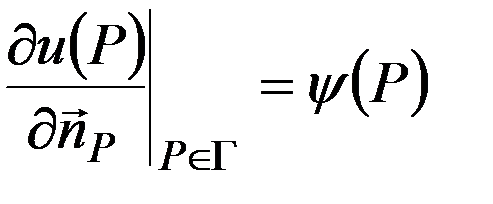 , (15)
, (15)  при
при 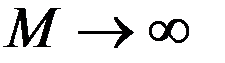 . (16)
. (16)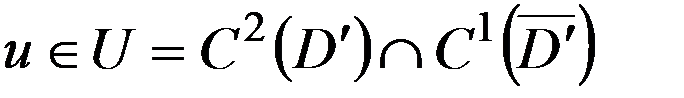 внешней задачи Неймана (12)-(14), тогда оно единственно в пространстве
внешней задачи Неймана (12)-(14), тогда оно единственно в пространстве 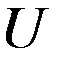 .
.


