
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Системы д.у в частн. производн.
Опр.1 Системой д.у с частн. произв. относит. Рассм. теперь сист. д.у с частн. произв. 1го порядка, стостоящ. из двух ур-ий, содерж. две неизвестн. ф-ии с 2мя незав.-ми перем-ми: В матричн. записи д.у (2) приним. вид вектор-столбец Для классиф. д.сист. (2) выделим ее главн. часть: Далее поставим в соотв. главн. части д.сист. (2) характер. матр.: и характ. многочлен: Классиф-ция д.сист. (2) приводится с помощью дискриминанта Пр.1 Рассм. аналитичн. ф-ию комплексн. перем-го эллиптич. сист. Коши-Римана для которой характ. матр. 1.Основные понятия о ду с частными производными. Рассмотрим n-мерное прос-о Опр1. Множество:1)m раз непрер-о диф-х на обл.
Опр2. Ду с частными произ-ми наз. соотношение где х независимые переменные,u=u(x) незав. фун-я, В ду с частными произв.,в отличае от обыкнов. ду,произв. эл. общего реш.,т.е. решения,из которых получаются все частные решения явл. Не произв. постоянными, а произвольными функциями. В общем случае число произв. функций будет равно порядку ду.В случае ду с n неизв. Переменными произв. функции будут ф-ми n-1 переменных.Общее решение представленное в неявном виде,будет наз. общим интегралом ду. Любое ду с частными произ-ми имеет бесконечное мн-о решений.Поэтому из выделения этого мн-а конкретного решения необходимы допол. условия. Краевые условия, заключ-ся в указании поведения решения на некоторой граничной линии или в её окр-ти.С этой точки зрения нач. условия представляют собой краевые условия во времени.Практически любая задача оприс. физ. процесс и сформулир. в терминах ду в частных произ-ых,включает в себя краевые условия. Пример1. Краевое условие u(x,0)=φ(x) может интерпретир. Как заданное в нач. момент времени темпер-а распред. в стержне.
Пример2. Под условием Дирихле понимают задание функции u(x,y,t) в каждой точке границы области в начальный момент времени.В частности условие Дирихле в круге R=1 имеет вид u(r,φ)r=R=f(φ),где r и φ есть полярные координаты точки (х,у), f(φ) заданные функции. Пример3.Условие Неймана подразумевают задание нормальной компоненты градиента (∆u)n в каждой точке границы. Пример4.Условие Коши представляет собой сочитание условий Дирихле и условий Неймана и одноз. задание фун-ии (х,у,t) и проекции градиенты этой функции на нормаль в каждой точке границы в начальный момент времени.
|
|||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 169; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.150.55 (0.007 с.) |
 неизвестн. ф-ий
неизвестн. ф-ий 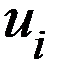 ,
,  ,буд наз. систему из
,буд наз. систему из 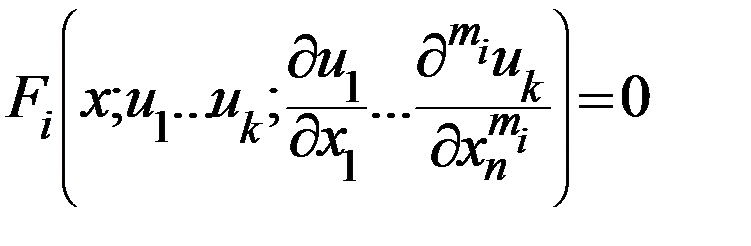 (1)
(1)
 (2)
(2) , где матричн. д.оператор:
, где матричн. д.оператор:  ,
, ,
, 


 , где
, где  ,
,  ,
, 
 характ. многочлен по аналогии с классифик. д.у:
характ. многочлен по аналогии с классифик. д.у: 

 ,характ. многочлен
,характ. многочлен  , а дискриминант
, а дискриминант 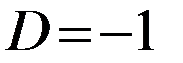 .
. .Пусть область
.Пусть область  .Зададим на R ф-ю u=u(x),x=(x1,…,xn).
.Зададим на R ф-ю u=u(x),x=(x1,…,xn). функций обозначаем через
функций обозначаем через  ;2)любое число раз непр-о диф-их на обл.
;2)любое число раз непр-о диф-их на обл.  ;3)аналитич. на обл.
;3)аналитич. на обл.  .Через
.Через  ,
, будет обозначать мн-о функций
будет обозначать мн-о функций  ,огранич. на обл.
,огранич. на обл.  , (1)
, (1) ,…,
,…,  ,…,
,…,  .Число m порядок ду(1). Опр3.Классическим решением ду(1) на обл.
.Число m порядок ду(1). Опр3.Классическим решением ду(1) на обл.  ,обращающая ду (1) в тождество на
,обращающая ду (1) в тождество на 


