
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Постановка смешанных задач для уравнения теплопроводности.
На плоскости R2 c координатами X,t выделим область D= (0<x<l)X(0<t<+∞). На этой области рассм. ур. теплопроводности.
При данных функциях f,ϕ,µ1,µ2 требуется найти функцию найти функцию u которая удовлетворяет ДУ (19.2) начальному усл. (19.3) и граничными усл.(19.4) Условие согласования в данном случае имеет вид
Задача (19.2)-(19.4) описывает процесс распрост. тепла в тонком стержне длины l, располож. вдоль отрезка (0<x<l). Функция u(x,t) задает температуру стержня в сечении x в момент времени t. Граничные условия (19.4) означают, что в торцах стержня x=0, x=l поддерживается заданная температура µ1(t),µ2(t) соответственно. Функция ϕ(x) в начальном условии (19.3) задает температуру стержня в каждом сечении X в начальный момент времени t=0. Вторая смешанная задача для ур. теплопроводности имеет вид
Условия (19.7)наз. граничными условиями 2-го рода. Условия соглас. в данном случае имеет вид:
Граничные условия(19.7) означают, что в торцах стержня x=0, x=l задан тепловой поток. Третья смешанная задача для ур. теплопроводности имеет вид
Граничные условия(19.10) моделируют теплообмен стержня через торцы x=0, x=l с окружающей средой.
Решение методом разделения переменных первой смешанной задачи для однор. ур. теплопроводности. Рассм. 1-ую смешанную задачу для однородного ур. теплопроводности с однородными граничными условиями
Условия согласования в данном случае имеют вид ϕ(0)= ϕ(t)=0. Для решения задачи (20.1)- (20.3) применим метод разделения переменных. Будем искать решения ур.(20.1) в виде
Подставим выражение (20.4) в ур. (20.1) и разделив получим соотношения
Потребуем чтобы решения(20.4) удовлетв. граничным условиям (20.3).Подставив(20.4) в (20.3) получим
Общее решение данного ДУ имеет вид
Из этих решений составим общее решение в виде ряда
Вычислим Аn удовлетворяя начальному условию(20.2). Имеем получаем, что
|
|||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 1004; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.243.32 (0.007 с.) |
 (19.1)Где u=u(x,t) есть искомая функция. Ур.(19.1) наз. также одномерным ур. теплопроводности. Первая смешанная задача для ур. теплопроводности имеет вид
(19.1)Где u=u(x,t) есть искомая функция. Ур.(19.1) наз. также одномерным ур. теплопроводности. Первая смешанная задача для ур. теплопроводности имеет вид
 (19.3)
(19.3) ,
,  (19.4)
(19.4)
 ,
, 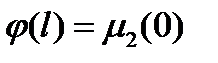
 (19.7)
(19.7) ,
, 


 , (19.10)
, (19.10) Условие согласования имеет вид
Условие согласования имеет вид ,
, 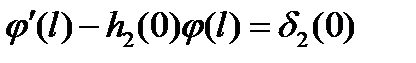
 (20.2)
(20.2) ,
,  ,
,  (20.3)
(20.3) (20.4)
(20.4)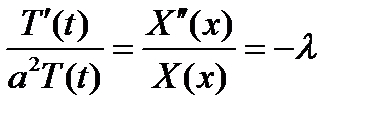 , где λ – постоянное разделение. В результате получим 2 обыкновенных ДУ.
, где λ – постоянное разделение. В результате получим 2 обыкновенных ДУ. (20.5)
(20.5) (20.6)
(20.6) ,
,  (20.7) Таким обр. нами получена задача Штурма-Лиувиля (20.6), (20.7) совпад. с задачей Штурма-Лиувиля. Вычислим теперь Tn(t) положив в ДУ (20.5) λ=λn, в результате получим ДУ
(20.7) Таким обр. нами получена задача Штурма-Лиувиля (20.6), (20.7) совпад. с задачей Штурма-Лиувиля. Вычислим теперь Tn(t) положив в ДУ (20.5) λ=λn, в результате получим ДУ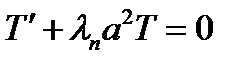
 ,
,  ,где Аn есть произв. постоянная. В результате мы получим бесконечную последовательность частных решений вида (20.4) ур. (20.1) удовлетв. граничным условиям (20.3)
,где Аn есть произв. постоянная. В результате мы получим бесконечную последовательность частных решений вида (20.4) ур. (20.1) удовлетв. граничным условиям (20.3) (20.8)
(20.8)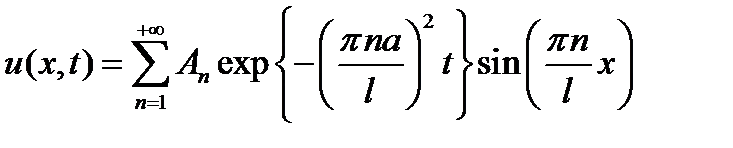 (20.9)
(20.9)
 ,
,  (20.10). Таким образом мы получим общее решение первой смешанной задачи (20.1)- (20.3) для ур. теплопроводности ряда (20.9) коэф. которого находятся по формулам(20.10).
(20.10). Таким образом мы получим общее решение первой смешанной задачи (20.1)- (20.3) для ур. теплопроводности ряда (20.9) коэф. которого находятся по формулам(20.10).


