
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Классификация ДУ-ий в частных производных 2-ого порядка с двумя независимыми переменными.
Многие физ. задачи приводят к ду в част. произ-ых 2-го порядка относит-о искомой функции.Общий вид таких ду след.: Линейное ду отн-но старших произ-ых имеет вид:
Рассмотрим ду (1) в случае двух независимых переменных,имеет вид: где вещ-ые функции аij зависит только от независимых переменных x и y и опр-ся на обл. D.Так же будем считать,что на этой обл. все коэф. аij одновременно в 0 не обр-ся. Пусть Отобр-ие (4) будем подбирать так,чтобы в новых перем-х ду (3)имело наиболие простой вид.Преобр-ем ду (3) к новым переменным пологая
24.Решение задачи Дирихле для круга методом разделения переменных. На пл-ти
Требуется найти решение
Задачу (3), (4) решим методом разделения пер. Найдем все реш. ур-ния Лапласа (3) вида: Разделим это равенство на Выраж слева зависит только от В результате получим два обыкновенных д. у.: Рассмотрим случай, когда Рассмотрим случай, когда
Общие реш этих ур: После подстан. ф-ций (7), (8) в (5) получим частные реш ур-ния Лапласа в пол.коорд: из смысла задачи (3), (4) решение
Образуем общ реш д.у. (4.36) в виде лин комбинации частных реш (10): Коэффициенты условия (4). Подставляя (11) в (4), получим
Разложим функцию Приравнивая ряды (12) и (13), вычисляем коэффициенты Подставив коэффициенты в разложение (11), получим решение исходной задачи Дирихле (1), (2):
Можно показать, что ряд (15) равномерно сходится. Если подставить интегралы (14) в (15) и просуммировать ряды, то получим решение задачи Дирихле для круга в виде интеграла: называемого интегралом Пуассона. Примеры некорректно поставленных задач Коши 1)Зад. Коши для гиперб. ур-ния с нач. усл. на хар-ке. Рассм. зад. Коши:
где Предпол., что зад. Коши (1), (2) имеем реш.
Учитывая второе условие (2), получ. необх. Усл. разрешимости зад. Коши (1), (2)
Если усл. (3) не вып., то зад. (1), (2) не имеет решение. Построим реш. зад. Коши (1), (2), предполагая, что усл. (3) выполнено. Воспольз. общим реш. (5.2) ДУ (1), где ф-ции Из 1-го нач. усл. получим, что
Положим Тогда второго нач. усл. получ., что
Учитывая усл. разрешимости (3), получим соотношение Общий вид такой функции
где произвольная функция Т.о., получено реш. зад. Коши (1), (2) в виде:
к-рое не единственно в силу произвольности функции В итоге приходипм к выводу, что задача Коши (1), (2) поставлена некорректно, т.к. не вып. 1-е или 2-е усл. корректности из опр. (10.2). 2)Зад. Коши для параболического уравн. с нач. усл. на хар-ке. Рассмотрим задачу Коши
Предпол., что классич. реш. зад. (4), (5) сущ. для обл.
|
||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 269; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.235.196 (0.014 с.) |
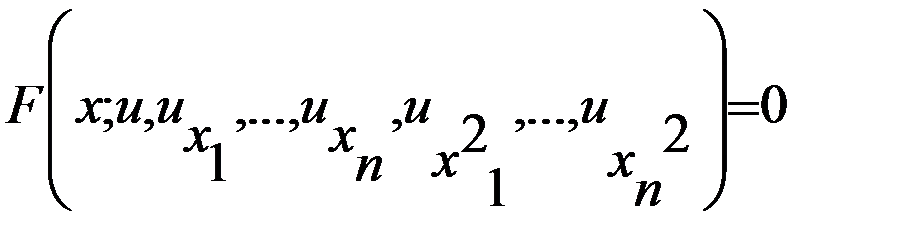 .
. где коэфиц. аij явл. только фун-ми независимых переменных х.Если они зависят также и от искомой функции u и её первых частных производных,то ду (1) наз. квазилинейным.Ду (1) наз. линейным,если оно линейно не только относительностарших роизводных,но и относительно искомой функции и её первых частных произ-ых.Такое ду имеет вид:
где коэфиц. аij явл. только фун-ми независимых переменных х.Если они зависят также и от искомой функции u и её первых частных производных,то ду (1) наз. квазилинейным.Ду (1) наз. линейным,если оно линейно не только относительностарших роизводных,но и относительно искомой функции и её первых частных произ-ых.Такое ду имеет вид:

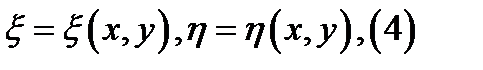 где ξ и η дважды непрер-о диф-мы на обл. D.Преобр. (4) осущ-ет взаимно однозначное отобр-ие обл. D на обл.G.Нужно,чтобы якобиан перобр. (4) ≠0:
где ξ и η дважды непрер-о диф-мы на обл. D.Преобр. (4) осущ-ет взаимно однозначное отобр-ие обл. D на обл.G.Нужно,чтобы якобиан перобр. (4) ≠0:  .
. В новых перем. ду (3) примен. вид:
В новых перем. ду (3) примен. вид:
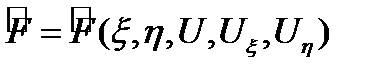 есть функция не зав-ая от старших произ-ых. Проверкой убеждаемся,что
есть функция не зав-ая от старших произ-ых. Проверкой убеждаемся,что  Соот-я (4)-(10) позв. ввести след. классиф-ю квазалинейных ду (3),линеёных относительно старших производных. Опр1. Если в точке М0(х0,у0):1)выражение а122-а11а22>0,то ду (3) наз. ур. гиперболического типа в точке М0(х0,у0);2) выражение а122-а11а22=0,то ду (3) наз. ур. параболического типа в точке М0(х0,у0);3) выражение а122-а11а22<0,то ду (3) наз. ур. эллиптического типа в точке М0(х0,у0).Согласно (10) при любой невыр-ой замене (4) незав. перем. типа ду(3) не изменяется.Поэтому он явл. инвариантом при невыр-ых заменах незав. перем-ых.Это позволяет ввести такие ограничения. Опр2. Если тип ду(3) одинаково во всех точках обл.D,то наз. уравнение данного типа во всей обл-и. Опр.3. Если в разных точках обл. D ду(3) принадлежит разным типам,то наз. ур. смешенного типа на этой обл. Замечание: Рассмотрим квадр. форму,сост. из старших коэф-в ду(3),взятых в точке М0(х0,у0):
Соот-я (4)-(10) позв. ввести след. классиф-ю квазалинейных ду (3),линеёных относительно старших производных. Опр1. Если в точке М0(х0,у0):1)выражение а122-а11а22>0,то ду (3) наз. ур. гиперболического типа в точке М0(х0,у0);2) выражение а122-а11а22=0,то ду (3) наз. ур. параболического типа в точке М0(х0,у0);3) выражение а122-а11а22<0,то ду (3) наз. ур. эллиптического типа в точке М0(х0,у0).Согласно (10) при любой невыр-ой замене (4) незав. перем. типа ду(3) не изменяется.Поэтому он явл. инвариантом при невыр-ых заменах незав. перем-ых.Это позволяет ввести такие ограничения. Опр2. Если тип ду(3) одинаково во всех точках обл.D,то наз. уравнение данного типа во всей обл-и. Опр.3. Если в разных точках обл. D ду(3) принадлежит разным типам,то наз. ур. смешенного типа на этой обл. Замечание: Рассмотрим квадр. форму,сост. из старших коэф-в ду(3),взятых в точке М0(х0,у0):  Не трудно видеть,что классиф. ду(3) совпадает с классиф. квадр. формы (11).
Не трудно видеть,что классиф. ду(3) совпадает с классиф. квадр. формы (11).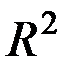 с коорд.
с коорд.  рассмотрим круг
рассмотрим круг  радиуса
радиуса  , описанный вокруг начала координат
, описанный вокруг начала координат  (0,0). Граница круга –окружность
(0,0). Граница круга –окружность 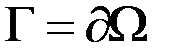 . Для круга сформул. внутр. задачу Дирихле для ур-ния Лапласа:
. Для круга сформул. внутр. задачу Дирихле для ур-ния Лапласа:  в обл.
в обл.  , (1) с граничн.усл.
, (1) с граничн.усл.  , (2)где
, (2)где 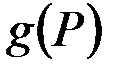 - заданная функция на окружности
- заданная функция на окружности  .
. .В полярных координатах:
.В полярных координатах: 
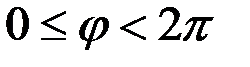 , задача (1), (2) запишется в виде:
, задача (1), (2) запишется в виде:  ,(3)
,(3)
 (4)
(4) (5).Подставив (5) в д.у. (3), получим равенство
(5).Подставив (5) в д.у. (3), получим равенство 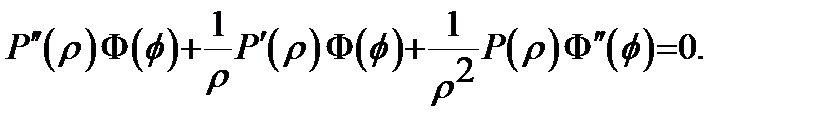
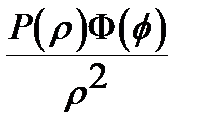 , отделяя ф-ции зависящ от
, отделяя ф-ции зависящ от  и ф-ции зависящ от
и ф-ции зависящ от 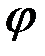 , тогда
, тогда 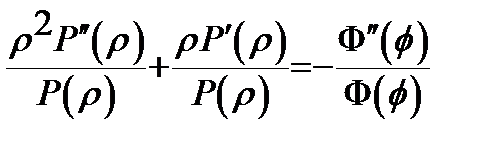 .
. , а справа - только от
, а справа - только от  , поэтому это рав-во имеет место ó, когда эти выраж явл.постоян, т.е.
, поэтому это рав-во имеет место ó, когда эти выраж явл.постоян, т.е.  где
где  -постоянная разделения.
-постоянная разделения.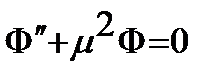 , (6)
, (6)  .
. . Общие реш ур(6)опред ф-ми:
. Общие реш ур(6)опред ф-ми:  (7)
(7)  ,где
,где  - произвольные постоянные.
- произвольные постоянные.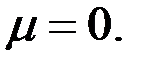 Ур.(6) примут вид
Ур.(6) примут вид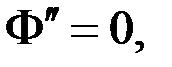
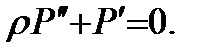
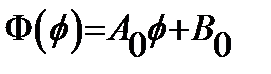 ,
, 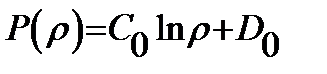 ,(8)где
,(8)где 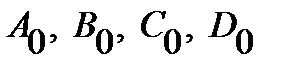 - произвольные постоянные.
- произвольные постоянные. (9)
(9) 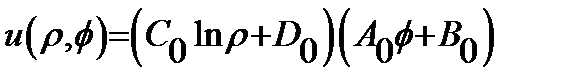 .
.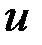 должно быть периодическим по углу
должно быть периодическим по углу 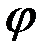 с периодом
с периодом 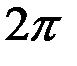 , т.е.
, т.е. 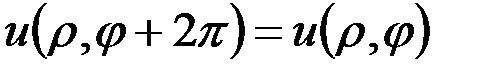 . Усл периодичности для ф-ций (9) будет выполнено, если
. Усл периодичности для ф-ций (9) будет выполнено, если 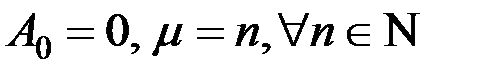 .В результате получим следующие частные решения д.у. (3):
.В результате получим следующие частные решения д.у. (3):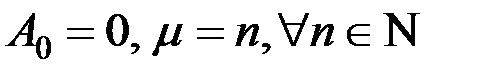 ,
,  ;
;
 (10)
(10)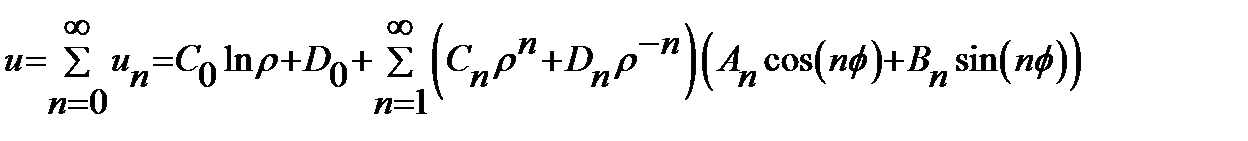 По смыслу зад Дирихле реш
По смыслу зад Дирихле реш 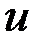 должно быть огранич в центре круга
должно быть огранич в центре круга 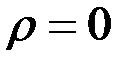 . Следовательно:
. Следовательно:  В результ получим представление реш задачи (3), (4) в виде разложения в ряд
В результ получим представление реш задачи (3), (4) в виде разложения в ряд 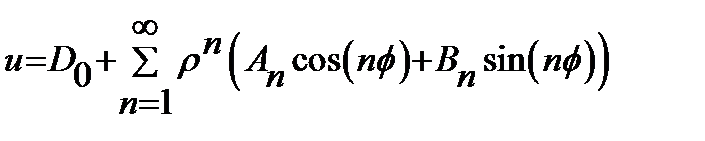 (11)
(11) определим из граничного
определим из граничного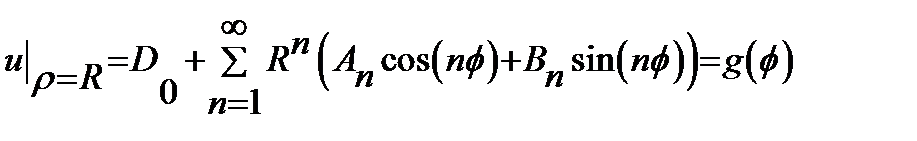 . (12)
. (12)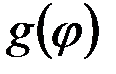 в ряд Фурье
в ряд Фурье 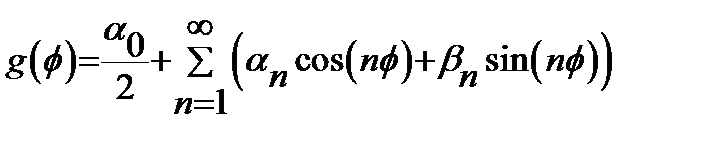 ,(13)где
,(13)где 
 (14)
(14)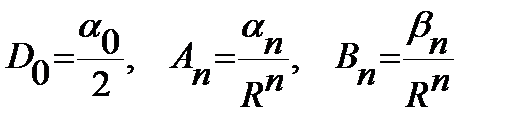 .
. (15)
(15)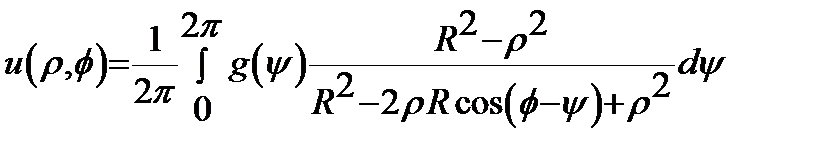 ,
, на
на 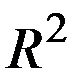 (1)
(1) (2)
(2)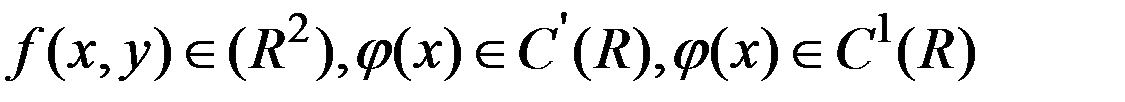 .
.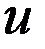 , облад. непрер. смешанной произв.
, облад. непрер. смешанной произв. 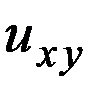 в области
в области 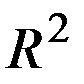 . Т.к. линия
. Т.к. линия  принадлежит области, то ДУ (1) должно выполн.
принадлежит области, то ДУ (1) должно выполн. 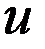 на линии, т.е.
на линии, т.е.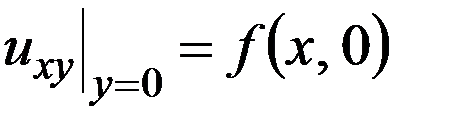 .
.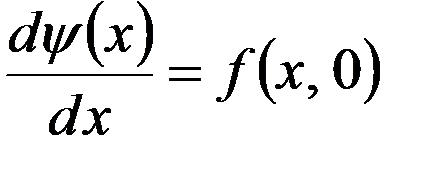 . (3)
. (3)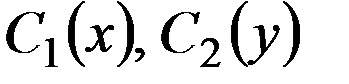 определим из начальных условий.
определим из начальных условий. .
.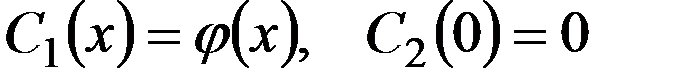 .
.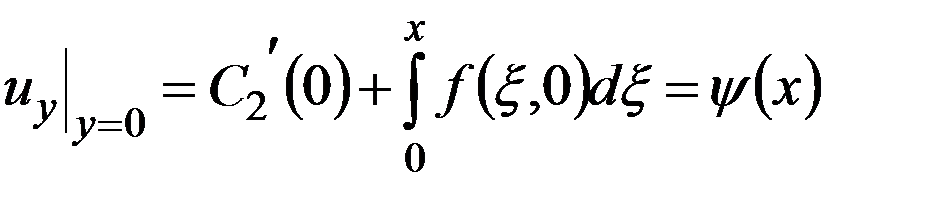 .
.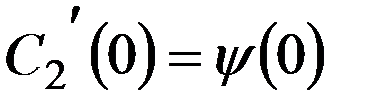 . Т.о. произв. ф-ция
. Т.о. произв. ф-ция 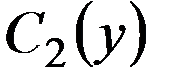 удовл. усл.
удовл. усл.  ,
, 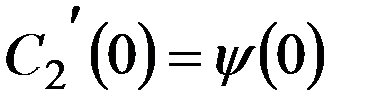 .
.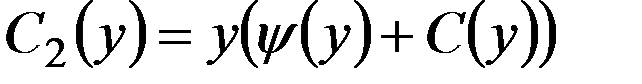 ,
,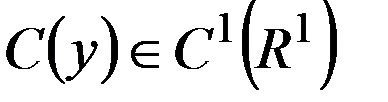 ,
, 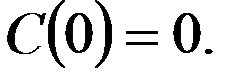
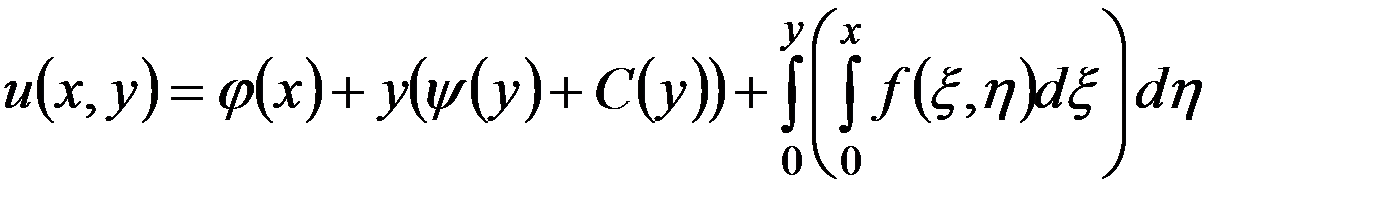 ,
,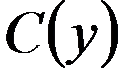 .
. на
на 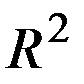 , (4)
, (4)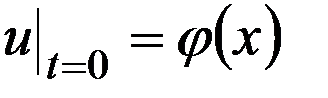 ,
,  ,
,  (5)
(5)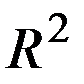 . Т.к. линия
. Т.к. линия 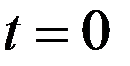 принадл. данной обл., то ДУ (4) должно выпол. и на линии, т.е.
принадл. данной обл., то ДУ (4) должно выпол. и на линии, т.е.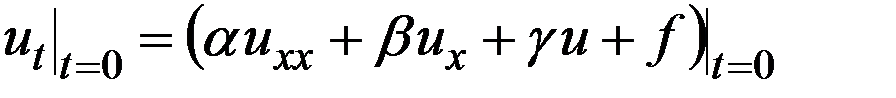 .
.


