
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вероятностная теория информацииСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
„Величайшее литературное произведение — в принципе не что иное, как ; разбросанный в беспорядке алфавит." Жан Кокто' ' В.2.1. Шенноновские сообщения „Тот факт, что зло всё ещё имеет более высокую информационную ценность, чем добро,— неплохой признак. Он доказывает, что добро по-прежнему является правилом, а зло, напротив, исключением." „Поезд, который сходит с рельсов, заведомо имеет большую информационную ценность, чем поезд, прибывающий по расписанию." Гастон Лакур Содержащаяся в сообщении информация может существенно зависеть от того момента времени, в который сообщение достигает приёмника. Задержка такого сообщения одновременно изменяет его характер. Примерами могут служить лотерейный билет, прогноз погоды и штормовое предупреждение. Предельным является случай, когда вся информация, которую несёт сообщение, определяется временем прибытия (заранее обусловленного) сигнала. Тогда говорят об извещении или тревоге. Примерами служат пожарный сигнал, звон колокола, бой часов или сигнал сирены. Существуют, однако, сообщения, информация которых не зависит от времени. Такие сообщения часто можно рассматривать как последовательности отдельных сообщений, которые посылаются друг за другом во времени: в момент времени t 0 — первое сообщение, в момент t1 — второе и т. д. Так как нас не интересует дальнейшая внутренняя структура отдельных сообщений, мы можем считать их знаками. Эти знаки считаются выбранными с некоторыми не зависящими от времени вероятностями из заранее заданного конечного или бесконечного набора знаков. Здесь нас особо интересует случай, имеющий место, например, при бросании кубика, когда вероятность встретить некоторый знак Z, в произвольный момент времени tсовпадает с относительной частотой знака Zво всей последовательности знаков. Последовательности знаков с таким свойством называются шенноневскими сообщениями, а порождающий их отправитель — источником сообщений или шенноновским источником. С математической точки зрения источник сообщений — это стационарный случайный процесс. Поскольку сами знаки и содержащаяся в них информация известны заранее, существенный момент при поступлении некоторого знака состоит в самом факте, какой именно из заданных знаков получен, т. е. какой из знаков был „выбран". Эти „выборы" исследуются теорией информации Шеннона. К. Шеннон в 1948 г. ввёл в связи с этим математическое понятие количества информации. Это в существенном мера тех затрат, которые необходимы для того, чтобы расклассифицировать („разобрать") переданные знаки. Слово „информация" употребляется здесь, очевидно, в некотором специальном смысле, не совпадающем с тем, в котором оно использовалось нами ранее. В.2.2. Количество информации Шенноновская теория информации, точнее количества информации, исходит из элементарного альтернативного выбора между двумя знаками (битами) О и 1_. Такой выбор соответствует приёму сообщения, состоящего из одного двоичного знака. По определению количество информации, содержащееся в таком сообщении, принимается за единицу и также называется битом. Если выбор состоит в том, что некоторый знак выбирается из множества п знаков, где При заданном выборочном каскаде нас интересует теперь, сколько потребуется альтернативных выборов для выбора какого-нибудь определённого знака. На рис. 1 приведён пример: чтобы выбрать а или е, нужны два альтернативных выбора (количество информации составляет 2 бита); чтобы выбрать b, с или f, необходимы три альтернативных выбора, и т. д. Если некоторый знак встречается часто, то, естественно, количество выборов, требующихся для его опознавания, стремятся сделать возможно меньшим. Соответственно для опознавания более редких знаков приходится использовать большее число альтернативных выборов. Другими словами, часто встречающиеся знаки содержат малое, а редкие знаки — большое количество информации. Поэтому представляется разумным разбивать исходное множество знаков не на равновеликие, а на равновероятные подмножества, т. е. так, чтобы при каждом разбиении на два подмножества суммы вероятностей для знаков одного и для знаков другого подмножества были близки друг к другу, насколько это возможно. Ради простоты будем считать сначала, что заданные вероятности позволяют получить точное равенство. Тогда если i -й знак выделяется после kiальтернативных выборов, то вероятность его появления рi равна
Рис.1. Выборочный каскад.
Тогда среднее количество информации, приходящейся на один произвольный знак, будет равно
Это — основное определение теории информации Шеннона. Величину Н называют средним количеством информации на знак, информацией на знак или энтропией источника сообщений. Результат одного отдельного альтернативного выбора может быть представлен как О или L. Тогда выбору всякого знака соответствует некоторая последовательность двоичных знаков О и L, т. е. двоичное слово. Мы назовем это двоичное слово кодировкой знака, а множество кодировок всех знаков источника сообщений — кодированием источника сообщений. Получающиеся двоичные слова имеют, вообще говоря, разную длину: знаку, вероятность которого рi, соответствует слово длины Ni = ld(1/рi). Однако условие Фано (см. 1.4.3) при этом выполняется автоматически. Таким образом, Н является еще и средней длиной двоичных слов, используемых при двоичном кодировании источника сообщений. На рис. 2 показано, как производится кодирование для примера, приведённого на рис. 1.
Рис.2. Оптимальное кодирование.
Если количество знаков представляет собой степень двойки, п = 2N и все знаки равновероятны, pi=(1/2)N, то все двоичные слова имеют длину N и H=N=ldn Легко показать, что для источника сообщений с п знаками и произвольными значениями pi. Равенство достигается в случае равновероятных знаков. Но даже в этом случае ld п — это, вообще говоря, не целое число. Это значит, что ld п не может быть (одинаковым для всех знаков) количеством необходимых альтернативных выборов. Тем не менее выбор из п знаков всегда можно осуществить с помощью N альтернативных выборов, где
Для этого достаточно разбивать всякое множество знаков так, чтобы количества знаков в двух получающихся подмножествах различались не более чем на 1. Таким образом, для источника с п знаками всегда существует кодирование словами длины N, где Несмотря на сказанное, имеет смысл использовать основное определение количества информации, содержащейся в знаке, и тогда, когда вероятности не являются целочисленными (отрицательными) степенями двойки или когда нельзя произвести точного разбиения на равновероятные подмножества. Если при некотором кодировании источника сообщений i -й знак имеет длину Ni то средняя длина слов равна
Наложив на набор знаков то ограничение, что его можно разбить на точно равновероятные подмножества, мы установили выше, что I. — Я. В общем случае связь между средней длиной слов Ь и энтропией Н источника сообщений даёт следующая Теорема кодирования Шеннона (Шеннон, 1948г.). 1. Имеет место неравенство
2. Всякий источник сообщений можно закодировать так, что разность L — Н будет как угодно мала. Чтобы получить кодирования, о которых говорится в пункте 2 теоремы, следует не просто кодировать каждый знак по отдельности, а рассматривать вместо этого двоичные кодирования для пk групп по и знаков. Тогда длина кода i -го знака Ziвычисляется так: Ni=(средняя длина всех кодовых групп, содержащих Zi) / k. Чем больше берётся k, тем точнее можно приблизиться к разбиению на равновероятные подмножества. Часто уже при k=2 или k=3 достигается практически приемлемое приближение. Именно теорема кодирования является оправданием для определения энтропии по формуле Н — это нижняя граница для количества затрачиваемых альтернативных выборов при наилучшем возможном кодировании. Разность L — H называют избыточностью кода, а 1—(H/L) — относительной избыточностью кода. Последняя задаётся обычно в процентах. Избыточность — это мера бесполезно совершаемых альтернативных выборов. Так как в практических случаях отдельные знаки почти никогда не встречаются одинаково часто, то кодирование с постоянной длиной кодовых слов в большинстве случаев избыточно. Несмотря на это, такое кодирование применяют довольно часто, руководствуясь техническими соображениями, в частности возможностью параллельной и мультиплексной передачи.
|
|||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 576; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.206.88 (0.007 с.) |

 то это можно сделать посредством конечного числа следующих друг за другом альтернативных выборов в форме выборочного каскада: данное множество из п знаков разбивается на два (непустых) подмножества, каждое из которых точно так же разбивается дальше, пока мы не получим одноэлементные подмножества.
то это можно сделать посредством конечного числа следующих друг за другом альтернативных выборов в форме выборочного каскада: данное множество из п знаков разбивается на два (непустых) подмножества, каждое из которых точно так же разбивается дальше, пока мы не получим одноэлементные подмножества. . Обратно, для выбора знака, который встречается с вероятностью рi требуется ki = ld(1/рi) альтернативных выборов. Исходя из сказанного мы определим количество информации, содержащейся в знаке, задаваемое частотой появления такого знака, как
. Обратно, для выбора знака, который встречается с вероятностью рi требуется ki = ld(1/рi) альтернативных выборов. Исходя из сказанного мы определим количество информации, содержащейся в знаке, задаваемое частотой появления такого знака, как  (бит).
(бит).
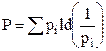 (бит).
(бит).



 .
. ; действительно,
; действительно,


