Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Редактор формул Microsoft Equation, MathTypeСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Технология работы 1. Запустить MS Word и создать новый документ. Ввести следующий текст: «Для ввода сложных формул в MS Word используется компонент Microsoft Equation. Более полная и мощная версия редактора Equation Editor — редактор формул MathType. Пользователи, которым часто приходится включать формулы в документы, предпочитают работать с MathType. Этот редактор так же прост в использовании, как и Equation Editor, однако имеет ряд дополнительных возможностей, ускоряющих работу и повышающих качество документов. MathType предоставляет следующим возможности: • создание формул для документов Web; • сохранение часто используемых формул, символов и шаблонов. Для последующей вставки их в документ достаточно один раз щелкнуть мышью; • преобразование формул на другие языки, такие как ТеХ; • добавление команд автоматического форматирования, обновления, нумерации и др. в меню MS Word; • выбор команд с клавиатуры». 2. Вставить формулу, для чего установить курсор в конец текста и выбрать на вкладке Вставка команду Объект. В окне Вставка объекта выбрать вкладку Создание, в списке вставляемых типов объектов выбрать Microsoft Equation и щелкнуть ОК. После этого на экране развернется панель инструментов Формула, показанная на рисунке 14, в которой имеется две строки инструментов. В верхней строке панели можно выбрать более чем 150 математических символов. В ее нижней строке содержатся шаблоны и наборы, в которых можно выбирать специальные символы (дроби, интегралы, суммы и т. д.).
Рис.14. Панель инструментов Редактор формул С помощью формульного редактора наберите формулу:
Технология работы: - вызовите формульный редактор; - в палитре шаблонов выберите третий слева шаблон с индексами; - в открывшемся списке выберите левый в первом ряду; - наберите греческое "Хи" (в палитре символов второе поле справа – греческие символы). Обратите внимание на различный вид курсоров. Вводимый символ вставляется в позицию, определяемую вертикальной чертой курсора! - подведите курсор в поле верхнего индекса и нажмите 2; - введите "=" после Х; - из палитры шаблонов выберите знак суммы с верхним и нижним индексами и введите индексы; - выберите из палитры шаблонов объект с верхним индексом (первый в четвёртом ряду);
- выберите шаблон со скобками; - выберите шаблон для дроби; - выберите шаблон с нижним индексом, введите "Хи", переведите курсор в следующую позицию (стрелкой - в знаменателе введите "s" - в месте верхнего индекса наберите "2"; - выйдите из редактора формул, щёлкнув левой кнопкой мыши вне поля редактирования. - сохраните формулу в файле. Наберите систему линейных уравнений в матричной записи в виде:
Технология работы: - в новом окне вызовите формульный редактор; - из палитры шаблонов выберите круглые скобки; - выберите шаблон матрицы размером 4 - перемещаясь от поля к полю с помощью мыши или клавиши Tab, заполните матрицу; - выберите круглые скобки, вектор размером 4, заполните его значениями; - введите "="; - аналогично введите последний вектор; - выйдите из редактора формул; - сделайте подпись под матрицей; - сохраните рисунок в файле. 3. Выйти из режима редактирования формул и вернуться в редактор MS Word, щелкнув в любом месте документа MS Word вне рамки с формулой. Задание для самостоятельной работы. 1. Формула для вычисления определенного интеграла:
2. Коэффициент автокорреляции:
3. Формула расчета функции титрования:
4. Формула расчета волновой функции:
5. Матрица гамильтониана при наличии магнитного поля:
6. Формула расчета наименьшего обнаруживаемого числа парамагнитных центров в резонаторе ЭПР:
7. Связывающая молекулярная орбиталь, содержащая
8. Двухэлектронная волновая функция:
9. Наберите формулы:
ЛАБОРАТОРНАЯ РАБОТА № 11
|
|||||
|
Последнее изменение этой страницы: 2016-12-17; просмотров: 852; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.182.201 (0.007 с.) |



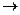 или щелчком мыши), наберите "–", затем "m"
или щелчком мыши), наберите "–", затем "m"
 4;
4;





 электроны:
электроны: