Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные этапы опроса экспертов.Содержание книги
Поиск на нашем сайте
1. Уточнение объекта опроса. Получение новых мнений, рекомендаций, путей нового подхода к решаемой проблеме. Цель этого этапа – собрать всю информацию об исследуемом объекте и выделить наиболее существенные характеристики и ограничения. 2. Вероятностная оценка рабочей модели, ее характеристика, факторы, влияющие на нее. На этом этапе получают информацию, необходимую для выработки решения. Но на этом этапе информация не может быть сразу использована из-за несогласованности экспертных оценок. 3. Согласование оценок экспертов. Это этап может повторяться несколько раз, пока не будет достигнута достаточная согласованность мнений экспертов. После каждого этапа производится сбор, статистическая обработка и анализ результатов опроса. 25% самых высоких и 25% самых низких оценок отбрасываются. Перед каждым следующим этапом экспертов информируют о результатах предыдущего этапа. Они при этом могут пересмотреть или исправить предыдущие ответы. Если их оценки попали в отброшенные 25%, то их просят обосновать свое мнение (анонимно). Результаты опроса обрабатывают и вновь доводят до сведения экспертов, предоставив возможность опять пересмотреть оценки. Как правило, трех этапов бывает достаточно для получения хорошо согласованных оценок экспертов. Метод ранжирования Ряд объектов (показателей, факторов) в соответствии с выраженностью определенного признака называют ранжированным. Сам процесс упорядочения называют ранжировкой. Номер, который при этом получает каждый объект, называют его рангом. Так, наиболее значимый объект получает ранг, равный 1. Ранг 2 присваивается объекту, наиболее значимому среди оставшихся, и т.д. Если значимость объектов выражена с помощью количественных характеристик (чисел), то ранжирование можно производить, упорядочивая их по убыванию (возрастанию) этих чисел. Если объекты одинаково важны, они получают одинаковые ранги, называемые связными рангами. В практике ранжирования объектов следует отказаться от использования связных рангов. Запрет на связные ранги диктуется и характером объектов, и стремлением получить от экспертов более полную и объективную информацию в результате дополнительного анализа близких по значимости объектов.
Процесс упорядочения объектов в соответствии с выраженностью определенного признака называют ранжированием. Если значимость определенных признаков объекта выражена с помощью количественных характеристик (чисел), то ранжирование объектов осуществляется естественным образом. Можно упорядочить их по возрастанию или по убыванию этих чисел. Если же у исследуемых признаков объектов нет количественных характеристик, то для их ранжирования прибегают к помощи экспертов. Номер, который получает каждый объект, называется рангом. Наиболее значимый объект получает ранг 1. Наиболее значимый объект среди оставшихся объектов ранг 2 и т.д. Ранги, назначенные каждым экспертом, назовем индивидуальными. Ранги, которые получают объекты по результатам групповой экспертизы, назовем групповыми рангами. Рассмотрим пример. Пусть нужно произвести ранжирование m объектов F1, F2,…,Fm. Привлекаем n экспертов. Ранг, который i-му объекту присвоит j-й эксперт, обозначим rij. В результате опроса всех экспертов получим результаты, которые сведем в таблицу. Пусть необходимо произвести ранжирование m объектов F1; F2;… Fi; …; Fm с помощью n экспертов (j = 1,2,..., n). Обозначим rij ранг, которые присваивает i-му объекту j-й эксперт. В результате опроса экспертов получаем таблицу-матрицу размером m x n, то есть матрица индивидуальных рангов имеет n строк и m столбцов.
Символически такую матрицу принято обозначать:
В таблице следует предусмотреть четыре графы для результатов обработки исходных данных. Для установки групповых рангов ri (i = 1, 2,…, m), по которым и производится ранжирование данных объектов, определяется суммарный ранг Ri по каждому объекту:
логика исследований и соответствующие нормативные документы, требуют оценить достоверность полученной экспертной информации путём проверки согласованности экспертных оценок внутри рабочей группы. Для этого вычисляют значение размаха
и проверяют условие
Если условие Если условие
Здесь D — дисперсия Ri, Понятие дисперсии и среднего арифметического широко применяется в математической статистике. Они вычисляются по следующим формулам:
Условие (*) получено в предположении, что с вероятностью более 90% можно утверждать, что между экспертами существует согласованность оценок, достаточная для того, чтобы экспертную информацию можно было считать достоверной. Теперь наименьшей сумме рангов, т.е. наименьшему значению из Ri, присваивается ранг, равный 1, наименьшему из оставшихся Ri — ранг 2 и т.д. Иначе говоря, ранжирование объектов производим, упорядочивая их по возрастающим значениям Ri. Если условие (*) не будет выполнено, следует рассмотреть дополнительно вопросы по составу рабочей группы. Рассмотрим пример. Пусть при ранжировании m=4 объектов n=5 экспертами получены следующие результаты:
Оценим результаты ранжирования по первому методу. вычислим значение размаха:
проверим условие Проведем дополнительную проверку на согласованность экспертных оценок по более точной формуле.
Так как 22>17,25 (
Метод балльных оценок
Пусть нужно произвести ранжирование m объектов. Привлекаем n экспертов. Метод балльных оценок позволяет непосредственно находить относительные коэффициенты весомости объектов (или индивидуальные баллы) Wij. Wij – это оценка, которую дает j-й эксперт i-му объекту. Эта оценка выражается в долях 1 или в процентах. От каждого эксперта можно потребовать выполнения условия нормированности индивидуальных баллов:
Эксперт в процессе назначения оценок должен контролировать выполнение условия нормированности индивидуальных баллов. Это побуждает его постоянно сравнивать объекты между собой. При этом получается более обоснованное экспертное заключение. «Все познается в сравнениии!!!». По результатам опроса n экспертов строим матрицу индивидуальных относительных коэффициентов весомости Групповую оценку весомости i-го объекта
Для оценки достоверности результатов (то есть согласованности назначенных экспертами индивидуальных коэффициентов весомости) вводится величина
Здесь
Если Рассмотрим пример. Пусть 5 экспертов оценивают 4 объекта.
согласованность назначенных экспертами индивидуальных коэффициентов весомости считаем недостаточной.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-17; просмотров: 250; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.15.173.197 (0.008 с.) |

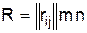 .
.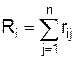 .
.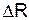 как разность между наибольшими и наименьшими значениями Ri:
как разность между наибольшими и наименьшими значениями Ri: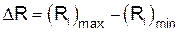
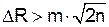 .
.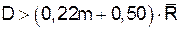 ,
, 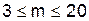 (*)
(*)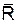 — среднее арифметическое Ri.
— среднее арифметическое Ri.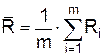 ,
, 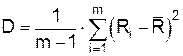 .
.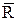
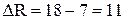 .
.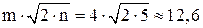 .
.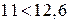 .
.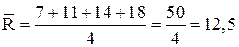 .
.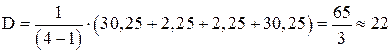 .
.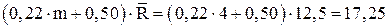 .
.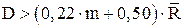 ), то можно утверждать, что между экспертами существует согласованность оценок, достаточная для того, чтобы экспертную информацию можно было считать достоверной.
), то можно утверждать, что между экспертами существует согласованность оценок, достаточная для того, чтобы экспертную информацию можно было считать достоверной.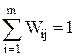 .
.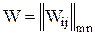 аналогичную матрице R (см. метод ранжирования).
аналогичную матрице R (см. метод ранжирования).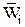 вычисляем следующим образом:
вычисляем следующим образом: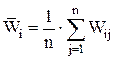 .
.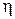 – относительный размах.
– относительный размах.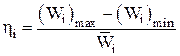 .
.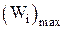 – наибольший индивидуальный коэффициент весомости из всех коэффициентов, данных экспертами по i-му объекту, то есть
– наибольший индивидуальный коэффициент весомости из всех коэффициентов, данных экспертами по i-му объекту, то есть 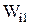 ,
, 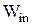 .
. 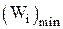 – наименьший индивидуальный коэффициент весомости из всех коэффициентов, данных экспертами по i-му объекту, то есть
– наименьший индивидуальный коэффициент весомости из всех коэффициентов, данных экспертами по i-му объекту, то есть 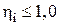 , то согласованность назначенных экспертами индивидуальных коэффициентов весомости считаем достаточной.
, то согласованность назначенных экспертами индивидуальных коэффициентов весомости считаем достаточной.