Глава 8. Основы алгоритмизации

 

Понятие алгоритма. Свойства и способы описания алгоритмов

 

Алгоритм – это конечная последовательность точно определенных действий, приводящих к решению поставленной задачи.

При составлении алгоритмов следует учитывать ряд требований, выполнение которых приводит к формированию необходимых свойств:

· алгоритм должен быть однозначным, исключающим произвольность толкования любого из предписаний и заданного полрядка исполнения. Это свойство алгоритма называется определенностью;

· любой алгоритм должен иметь только одно начало (один вход) и одно окончание (один выход);

· реализация процесса, предусмотренного алгоритмом, должна выдать результаты или сообщение о невозможности решения задачи. Это свойство алгоритма называется результативностью;

· способность алгоритма обеспечить решение однотипных задач с различными исходными данными. Это свойство называется массовостью;

· расчленение процесса, предусмотренного алгоритмом, на отдельные этапы, элементарные операции. Это свойство называется дискретностью.

Для строгого задания различных структур данных и алгоритмов, их обработки требуется иметь такую систему формальных обозначений и правил, чтобы смысл всякого используемого предписания трактовался точно и однозначно. Для выполнения этого условия или требования существуют следующие способы описания алгоритмов:

· словесное описание (запись на естественном языке);

· графическое описание;

· программное описание (тексты программ на алгоритмическом языке).

 

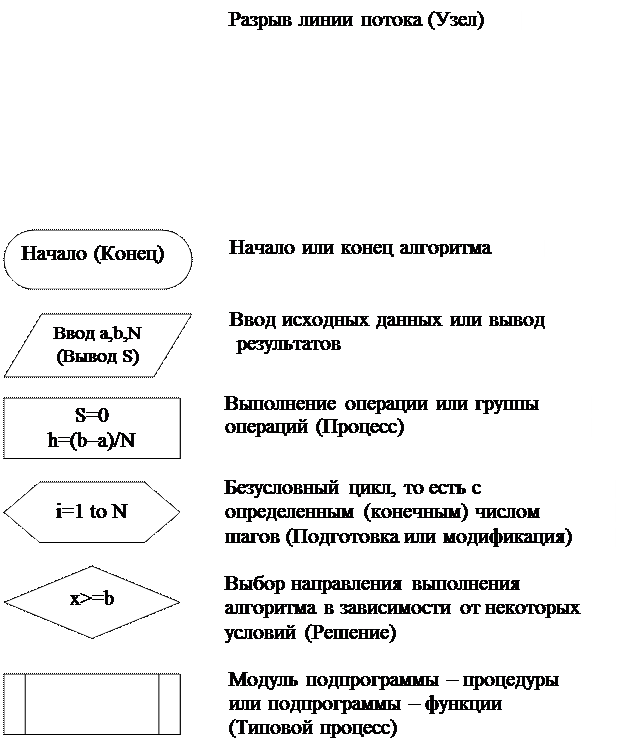
8.2. Графический способ описания (блок-схема)

Для составления алгоритма в виде блок-схемы применяются следующие основные графические изображения.

Графический объект	Предназначение объекта
	Начало или конец алгоритма
	Ввод исходных данных или вывод результатов
	Выполнение операции или группы операций (Процесс)
	Безусловный цикл (Модификация)
	Выбор направления в зависимости от условия (Решение)
	Подпрограмма ─ процедура или Подпрограмма ─ функция (Типовой процесс)
	Линия потока, соединяющая фигуры блок-схемы. Направление линии указывать при ее ходе слева направо. Изменение направления линии под прямым углом
	Разрыв линии потока (Узел)
	Ссылка на другую страницу

 

 

 

 

Базовые конструкции алгоритмов

 

При разработке и составлении блок-схемы того или иного алгоритма применяются следующие базовые конструкции: линейная, циклическая и ветвящаяся.

 

Линейная конструкция

Линейная конструкция – это последовательное выполнение операций без повторов и разветвлений.

Пример

 

 

Ветвящаяся конструкция

Ветвящаяся конструкция – это выполнение операций по одному из нескольких направлений в зависимости от заданных условий.

Пример

 

 

 

 

Циклические конструкции

 

Циклы используются для организации повторного выполнения какой-либо операции (инструкции) или блока операций (инструкций). Цикл состоит из двух частей: условие цикла и тело цикла. У любого цикла есть параметр. Параметр цикла – это переменная, которая изменяется в теле цикла, а также участвует в условии его окончания. Для организации повторов могут применяться следующие виды циклических конструкций: цикл с предусловием, цикл с постусловием, безусловный цикл (цикл с фиксированным количеством повторов или цикл по счетчику).

 

Цикл с предусловием

Конструкция цикла с предусловием в зависимости от результата выполнения условия может быть двух вариантов. В первом варианте повторение осуществляется до тех пор, пока условие имеет значение Истина (True). В другом варианте повторение осуществляется до тех пор, пока условие имеет значение Ложь (False).

Примеры:

Вариант 1	Вариант 2
Нет     Да	Да     Нет

 

Цикл с постусловием

 

Конструкция цикла с постусловием в зависимости от результата выполнения условия может быть двух вариантов. В первом варианте повторение осуществляется до тех пор, пока условие имеет значение Ложь (False). В другом варианте повторение осуществляется до тех пор, пока условие имеет значение Истина (True).

Примеры:

Вариант 1	Вариант 2
Да     Нет	Нет     Да

 

Безусловный цикл

 

В этом цикле выполнение и повторение операций происходит от начального значения параметра (счетчика) до его конечного значения с указанным шагом. Если шаг не указан, то его значение полагается равным единице.

Пример:

 

 

Простые циклические конструкции могут вкладываться в другую простую циклическую конструкцию, образуя тем самым вложенный (сложный) цикл. При этом необходимо выполнять следующие правила:

· имена параметров всех простых циклов не должны повторяться;

· нельзя войти во внутренний цикл, минуя внешний;

· простые циклы в сложном цикле не должны пересекаться, то есть внешний цикл должен заканчиваться после внутреннего (инструкции тела внешнего цикла не должны быть в теле внутреннего цикла).

Пример:

 

Вариант 1	Вариант 2

 

Базовые конструкции алгоритмов в чистом виде на практике не применяются, а используются в сочетании между собой.