Билет22 Изокоста и равновесие производителя в краткосрочном периоде.

Максимизировать выпуск при данных издержках позволяет прямая равных издержек - изокоста -комбинации ресурсов, использование которых ведет к одинаковым затратам. Рост бюджета производителя или снижение цен на ресурсы сдвигает изокосту вправо, а сокращение бюджета или рост цен - влево. Точка касания изокванты с изокостой дает равновесие производителя, т.к. позволяет достичь максимального объема производства при имеющихся ограниченных ресурсах, которые можно затратить на покупку ресурсов. Для нахождения точки равновесия производителя соеди­ним точки на оси абсцисс и оси ординат, в которых затраты на факторы производства будут равными. Получим изокосты. Теперь совместим изокванту с многочисленными линиями равных издержек. В точке B, где изокванта касается одной из линий равных издержек, издержки производства будут минимальными.

Равновесие производителя

Равновесие производителя - состояние производства, при котором использование факторов производства позволяет получить максимальный объем продукции, т. е. когда изокванта занимает самую отдаленную от начала координат точку. Чтобы определить равновесие производителя, необходимо совместить карты изоквант с картой изокост. Максимальный объем выпуска будет в точке касания изокванты с изокостой (рис. 21.6).

Рис. 21.6. Равновесие производителя

Из рис. 21.6 видно, что изокванта, расположенная ближе к началу координат, дает меньшее количество производимой продукции (изокванта Q1). Изокванты, расположенные выше и правее изокванты Q2, вызовут изменение большего объема факторов производства, нежели позволяет бюджетное ограничение производителя.

Таким образом, точка касания изокванты и изокосты (на рис. 21.6 точка Е) является оптимальной, поскольку в этом случае производитель получает максимальный результат.

 

Изокоста — линия, демонстрирующая комбинации факторов производства, которые можно купить за одинаковую общую сумму денег.

 

График изокосты

Изокосту иначе называют линией равных издержек. Изокосты являются параллельными прямыми, поскольку допускается, что фирма может приобрести любое желаемое количество факторов производства по неизменным ценам. Наклон изокосты выражает относительные цены факторов производства. Каждая точка на линии изокосты характеризуется одними и теми же общими издержками. Эти линии прямые, поскольку факторные цены имеют отрицательный наклон и параллельны.

Совместив изокванты и изокосты, можно определить оптимальную позицию фирмы. Точка, в которой изокванта касается (но не пересекает) изокосту, означает наиболее дешевую по стоимости комбинацию факторов, необходимых для выпуска определенного

Билет 23 Минимизация издержек производства

Одним из графических инструментов анализа производства является изокоста (рис.9).Изокоста - геометрическое место точек, соответствующих всем комбинациям двух ресурсов, которые имеют одинаковую стоимость.Изокоста аналогична бюджетной линии потребителя. Наклон изокосты постоянен вдоль всей прямой равен ценовому отношению обоих ресурсов.

Рис. 9 Изокоста

Ряд параллельных изокост характеризует разные уровни совокупных издержек при неизменных ценах факторов или при изменении цен в одинаковой пропорции. Если наклон изокосты меняется, это свидетельствует, при прочих равных условиях, об изменении цены одного из факторов (или об изменении цен обоих факторов, но в разных пропорциях).

Придерживаясь рационального принципа поведения, предприниматель стремится минимизировать издержки производства заданного объема продукции. Графическое решение этой задачи предполагает использование нескольких изокост и изокванты, соответствующей заданному объему производства. Для стандартной изокванты (производственной функции Кобба-Дугласа) решение обозначено на рис.9.1

рис. 9.1 минимизация издержек производства

Изокосты, лежащие ниже изокванты и не имеющие ней общих точек, означают, что заданный объем производства недостижим при столь низких уровнях издержек.Изокосты, пересекающие изокванту и имеющие с ней общие точки, означают, что уровень издержек завышен. Всегда можно подобрать иную комбинацию ресурсов, которая обеспечит заданный выпуск продукции при меньших затратах.Изокоста, проходящая по касательной к изокванте, характеризует тот минимальный уровень издержек, который требуется для выпуска заданного количества продукции. Точка касания заданной изокванты с возможно более низкой изокостой показывает ту комбинацию ресурсов, которую необходимо применять в данном случае. В точке касания углы наклона кривых равны, т. е. МР_L/МР_К — Р_L/Р_К.Графическим путем получена та же формула минимизации издержек, что и алгебраически.Кривая издержек показывает, какие минимальные издержки требуются для достижения нового масштаба производства. Тем самым кривая издержек показывает так называемую траекторию расширения фирмы.

Метод Лагранжа

Метод Лагранжа — метод приведения квадратичной формы к каноническому виду, указанный в 1759 году Лагранжем.

Описание

Данный метод состоит в последовательном выделении в квадратичной форме полных квадратов. Пусть

есть данная квадратичная форма. Возможны два случая:

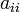1. хотя бы один из коэффициентов при квадратах отличен от нуля. Не нарушая общности, будем считать (этого всегда можно добиться соответствующей перенумерацией переменных);
2. все коэффициенты , но есть коэффициент , отличный от нуля (для определённости пусть будет ).

В первом случае преобразуем квадратичную форму следующим образом:

, где , а через обозначены все остальные слагаемые. представляет собой квадратичную форму от n-1 переменных . С ней поступают аналогичным образом и так далее.Заметим, что . Второй случай заменой переменных сводится к первому.