
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Применение теоретико-множественных представлений.Содержание книги
Поиск на нашем сайте
В рамках данного курса классическая теория множеств, представляющая собой применение теоретико-множественных представлений к теории чисел, не представляет особого интереса. Она может быть полезной лишь в качестве иллюстрации основных положений теоретико-множественных методов. Ниже обсуждается значение теоретико-множественных представлений описания состояний и процессов в сложных системах. При применении теоретико-множественных представлений для отображения сложных систем и процессов в них наиболее общими формальными характеристиками являются абстрактные знаковые формулы, с помощью которых удобно отображать многоуровневое строение систем. Например, система S может быть отображена в совокупность множеств, описываемую теоретико-множественной формулой: S = <I, C, A, P, E, U, X, W, Z>, где I = {i} – множество информаций, т.е. совокупность (общий вектор) входных информационных сигналов; A = {a} – множество выходных действий (актуаций) системы; E = {e} – множество элементов, из которых составлена данная система; U = {u} – множество отношений и элементов е; C = {c} – множество состояний (ситуаций) системы; X = {x} – множество признаков (или параметров), характеризующих состояние элементов и отношений; W = {w} – множество свойств свойств, т.е. w – свойства свойств системы: вес, цена, значимость каждого свойства по отношению к другим свойствам; P = {p} – множество вероятностей изменения состояний; Z = {z} – множество возмущений, действующих на систему. Представление системы полной формулой S = <I, C, A, P, E, U, X, W, Z> не всегда возможно и целесообразно. Обычно системы описываются сокращенными формулами (в зависимости от требований полноты и отображения), которые иногда носят следующие названия (в соответствии с количеством объединяемых множеств): – монада [I] или {i}; – диада (двойка) [I, A] или <{i}{a}>; – триада (тройка) [I, C, A] или <{i}{c}{a}>; – тетрада (четверка) [I, C, A, P] или <{i}{c}{a}{p}>.
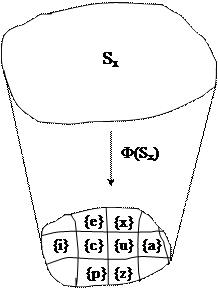
При отображении системы осуществляется декомпозиция её – выделение групп (множеств) элементов, обладающих одинаковыми (в рамках определенных ограничений) свойствами.
Выделив множества, можно производить соответствующие операции над ними, т.е., ставя их в определенные отношения друг с другом, прейти к композиции системы:
{x} R1 {c} R2 {e} Rj {u} Rk {a} Rn {i}
Символом R здесь обозначаются отношения между элементами или множествами в случае, если не определен характер этих отношений. Решение задачи композиции системы заключается в определении характера взаимоотношений между элементами или множествами, т.е. в замене символа R соответствующим знаком – оператором, функтором, - выражающим смысл и основные свойства отношений. Выяснение характера взаимоотношений между множествами или их элементами и возможные преобразования выражения {x} R1 {c} R2 {e} Rj {u} Rk {a} Rn {i} выполняются на основе определенных правил – законов, аксиом. Композиция обычно осуществляется путем задания отношений между элементами, принадлежащими различным множествам, например, <x, r, c> и образование этих пар (троек и т.д.) взаимодействующих элементов нового множества. Таким образом, теоретико-множественные формулы переводят систему Интересно отметить, что при конкретизации правил образования новых понятий теоретико-множественные представления могут привести к одной из алгебр логики, к одному из формальных языков математической лингвистики. В принципе при применении теоретико-множественных представлений допустимо введение любых отношений. Благодаря этому свойству, теоретико-множественные представления а) служат хорошим языком, с помощью которого облегчается взаимопонимание между представителями различных областей знаний; б) могут являться основой для возникновения новых научных направлений. В этом основное значение теоретико-множественных представлений. Частным случаем теоретико-множественных отображений являются логические отображения: система с языка реальности переводится на язык одной из алгебр логики (двузначной, многозначной, непрерывной).
Графические методы (Подоровский С.)
Графические методы являются удобной формой отображения систем, так как они позволяют наглядно представить процессы, происходящие в системах, что облегчает их анализ. Классификация применяемых в настоящее время графиков по признакам и видам приведена в таблице 9. Большинство графических примеров служит для наглядного представления информации. Однако некоторые из них позволяют решать вопросы оптимизации процессов организации и управления с применением строгих математических методов. Заслуживают внимания графические методы представления операций во времени. Старейшим из них является график Ганта (рис 9). На этом графике в прямоугольной системе координат «время-операция» наносятся сведения о выполняемых работах при планировании, контроле и управлении производством. График Ганта выполняется в форме чертежей, ленточных диаграмм с ручным управлением или ленточных диаграмм с автоматическим управлением. В двух последних случаях графики представляют собой бесконечные ленты, одна половина которых окрашена в черный цвет, вторая – в белый; причем черный участок в масштабе времени соответствует продолжительности операции. Дальнейшим шагом было разделение отрезка времени, отображающего дискретные операции, на дискретные элементы (рис 9б). Все операции и интервалы времени могут быть пронумерованы: операции I, II, III, IV, V; интервалы – 1, 2, 3,.. 19, 20, 21. В этом случае появляется возможность оперировать дискретной информацией. Можно вообще отойти от конфигурации ленточных графиков и рассматривать всю совокупность дискретных операций в дискретном времени, как множество событий, упорядоченных в двух измерениях. Это показано на рис. 9в. Последний вариант составляет переходное звено к современным сетевым графикам планирования, наблюдения и управления. В зарубежных работах соответствующие методы называются методом ПЕРТ (РЕРТ), в отечественной литературе принято название «Сетевое планирование и управление» (СПУ). В стилизованном виде, график СПУ показан на рис. 9г. В отличии от предыдущих вариантов, в нем добавлены стрелки связей, показывающие соотношение операций и моментов времени при выполнении каких-либо работ. Практически при построении графиков СПУ нарушают строгую геометрию рис 9г., так как удобнее «сшивать» операции во времени произвольным подсоединением групп операций.
Основная терминология сетевого моделирования.
При применении сетевых моделей пользуются определенной терминологией: вершина, ребро, путь. Эти понятия пояснены с помощью рис.10. Сетевые модели могут быть представлены: - в терминах работ (вершины отражают действия работы, ребра- события, результат работы); - в терминах событий (вершины отражают события – результат действия, операции, ребра – работы); - в терминах работы событий (смешанные), в этом случае ребра отражают только направление перехода от одной вершины к другой.
Часто применяют также термины источник и сток. Источником называют исходное событие (или работу), стоком – конечное событие. Сеть может иметь несколько источников и один сток (одноцелевые сети), один источник и несколько стоков (многоцелевые сети). При анализе сетей их оценивают по одному из критериев (например, по времени или стоимости и т.д.), а затем, суммируя оценки вершин (или ребер, в зависимости от вида сети), определят путь, наилучший с точки зрения данного критерия. Этот путь называют критическим.
Основным математическим аппаратом анализом сетевых графиков является теория графа. Теория графа – математическая теория, которая развивалась независимо от сетевого планирования. Основная терминология этой теории приведена в таблице 10. По предъявляемым к сетевым графикам требованиям (наличие истоков и стока, отсутствие циклов) они представляют собой направленный граф. Методы анализа таких графов для случая, когда ребра графа (работы сетевого графа) имеют детерминированные оценки, хорошо разработаны. В более сложных случаях – если граф вероятностный – решение не всегда может быть найдено. В ряде ситуаций такие графы путем введения статических оценок могут быть сведены к детерминированным. В других – к вероятностным графам, представляющим собой так называемые цепи Маркова.
|
||||||||||
|
Последнее изменение этой страницы: 2016-12-28; просмотров: 565; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.219.152.33 (0.008 с.) |

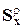 языка реальности в абстрактную систему, описываемую искусственным языком α, β или γ, имеющим соответствующий словарь (множество элементов, множество состояний, множество признаков и т.д., отображенных определенными символами) и правила образования новых понятий – композиций (множество отношений, законов, аксиом). Сложность языка определяется сложностью отображаемой системы и допустимой степенью абстрагирования.
языка реальности в абстрактную систему, описываемую искусственным языком α, β или γ, имеющим соответствующий словарь (множество элементов, множество состояний, множество признаков и т.д., отображенных определенными символами) и правила образования новых понятий – композиций (множество отношений, законов, аксиом). Сложность языка определяется сложностью отображаемой системы и допустимой степенью абстрагирования.


