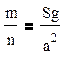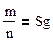Теория статистических испытаний

 

Теория статистических испытаний или статистического моделирования является особым методом получения статистических оценок анализа систем и процессов.

Она применяется для:

- решения статистических задач, в которых нахождение законов распределения или хотя бы вероятностных характеристик (дисперсии, коэффициента или функции корреляции, и др.) является очень сложной, практически неосуществимой задачей.

- Решения отдельных детерминированных задач или анализа систем, для которых в силу сложности вычислений решение не может быть получено аналитическими методами.

 

В этих случаях подбирается и моделируется на ЭВМ процесс, сходящийся к результату решения.

Теория статистических испытаний является распространением более специфического метода Монте-Карло на случай сложных систем и процессов и основана на законе больших чисел. В силу этого закона оценки, полученные на основе достаточно большого числа реализаций случайного процесса, приобретают статистическую устойчивость (порядок дисперсии оценки равен 1/n, n – число реализаций), и с достаточной для практики точностью могут быть приняты в качестве примерных значений искомой величины.

 

Идею метода статистических испытаний удобно пояснить на примере с геометрической интерпретацией вероятности.

Детерминированную площадь можно в принципе считать размытой точкой. Можно представить матрицу случайных попаданий детерминированной точки на измеряемую детерминируемую площадь (Двумерная матрица). Получается представление детерминированной площади стохастическим отображением.

, причём S Pij =1, 0 £Pij £1

Такие матрицы называют стохастическими.

Закон распределения определяется заданием значений Pij в матрице P.

Стохастическая матрица может быть решена с помощью алгоритма из логических операторов, когда результат выполнения Аi однозначно определяет оператор Aj, к которому следует перейти. Тогда Рij можно рассматривать как вероятность перехода от Ai к Aj.

Если удастся подобрать вероятности Pij и операторы Aj так, что какая-либо числовая характеристика закона распределения (например, МО) с ростом числа опытов будет сходиться по вероятности к исходному значению некоторой функции Y(x), то полученная схема алгоритма будет называться стохастическим алгоритмом, вычисляющим функцию Y(x).

Стохастический алгоритм называют методом статистических испытаний.

Рассмотрим применение метода Монте-Карло для вычисления площади произвольной фигуры G, находящейся внутри квадрата со стороной а.

 

Смоделируем случайный процесс L –бросание точки в квадрат. Тогда вероятность того, что точка попадёт внутрь фигуры G,будет равна отношению площади фигуры G к площади квадрата

G a

а

 

При увеличении числа бросков по формуле Бернулли получим

 

 

где n- число бросаний, m – число попаданий.

При достаточно большом числе испытаний с вероятностью, близкой к единице,

можно утверждать, что:

При а=1 получаем:

 

Чем больше n, тем больше точность этой оценки.

При решении задач на ЭВМ с применением метода Монте-Карло в некоторых случаях можно (даже выгодно) отказаться от моделирования истинно случайного процесса и пользоваться датчиком псевдослучайных чисел.

Некоторым усовершенствованием метода Монте-Карло являются методы случайного поиска с ограничениями, накладываемыми на выбор применяющихся операторов; метод Монте-Карло с адаптацией; когда учитываются ошибки (промахи и неудачи), оцениваемые по случайной выборке; а также статистические испытания с применение эвристических методов, сокращающих время решения.