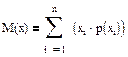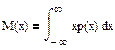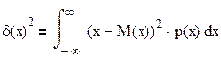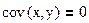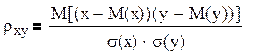Применение аналитических методов.

 

Аналитические методы применяются в тех случаях, когда свойства системы можно отобразить с помощью детерминированных величин или процессов. Эти методы используются при разрешении задач движения или устойчивости, оптимального решения, оптимального распределения работ и ресурсов, выбора оптимального пути, оптимальной стратегии поведения в конфликтных ситуациях и т.д.

Рассмотренные выше математические теории явились основой ряда прикладных теорий, таких как теория автоматического управления, теория оптимальных процессов, теория решений, теория исследования операций и т.д.

При применении аналитических методов для анализа задач, возникающих при разработке и организации функционирования сложных систем, нужно установить все детерминированные связи между компонентами (подлежащими выбору), учитываемыми критериями и задачами (формализующими цель системы) в виде аналитических зависимостей. Для задач, в которых учитывается много компонент и много критериев, это трудно осуществить. Более того, если даже это удается, то практически невозможно доказать правомерность применения этого аналитического выражения, то есть адекватность полученной аналитической модели рассматриваемой задаче.

Кроме того, в ряде случаев (в частности, при описании системы “документальный информационный поток”) в принципе нереально установить все связи между учитываемыми компонентами (информационными источниками) и целями (информационными потребностями, запросами).

В таких случаях возможны следующие подходы:

1. Не устанавливая всех детерминированных связей, на основе выборочного исследования получить статистические закономерности и распространить их с какой-то вероятностью на поведение системы в целом (т.е. применить статистические методы).

2. С помощью знаковой системы (“языка”) фиксировать явные простейшие связи и, комбинируя их, выявлять новые, неизвестные ранее. Иными словами, использовать то, что известно к моменту начала анализа задачи и, постепенно накапливая новые факты и связи, все более и более адекватно отображать систему и исследуемые в ней процессы.

 

 

Статистические методы (Гришина Е.)

 

Не всегда допустимо вводить такие жёсткие ограничения, которые позволили бы представить систему с помощью детерминированных категорий без ущерба для понимания свойств реальной системы.

Например, в тех случаях, когда:

- исследователю неизвестна программа, структура или поведение системы.

- Они настолько сложны, что невозможно описать их аналитически.

 

В этих случаях применяют статистические методы и говорят о случайных (стохастических) событиях, процессах, моделях.

Статистическое отображение системы можно представить в виде «размытой точки» в

N-мерном пространстве, совершающей какое-либо движение (поведение) системы.

Размытую точку следует понимать как некую область, характеризующую движение (поведение) системы, границы этой области заданы с некоторой вероятностью. Движение точки по этой области определяется не аналитическим выражением, а некоторой случайной функцией.

Закрепляя все параметры, кроме одного и исследуя поведение системы, можно получить разрез по линии ab, физический смысл которого- воздействие данного параметра на поведение системы в свободном движении, что можно описать статистическим распределением по данному параметру. В принципе существуют 2,3,.. n – мерные статистические распределения (по n осям).

Статистические распределения можно представить в виде ДСВ и их вероятностей или в виде НСВ, непрерывных случайных событий, непрерывных случайных процессов.

Закон распределения является удобной формой статистического отображения системы.

Для дискретного случая чаще всего закон распределения представляют в табличной форме:

X i	X1	…	Xn
P(xi)	P1	…	Pn

 

Для непрерывного случая:

1) В виде функции распределения F(x)

2) В виде плотности вероятности f(x)= F¢(x)

 

Практическое применение получили, в основном, одномерные распределения.

 

Однако определение закона распределения является трудной часто невыполнимой задачей, поэтому используется не сам закон распределения, а его характеристики - начальные и центральные моменты: математическое ожидание, дисперсия, ковариация (момент связи), коэффициент корреляции.

Математическое ожидание вычисляется по формуле:

Для дискретных величин:

Для непрерывных величин:

Дисперсия случайной величины

 

Для дискретных величин:

Для непрерывных величин:

На практике часто используется не дисперсия, а среднее квадратическое отклонение, то есть квадратный корень из дисперсии.

Связь между системами в общем случае характеризуется ковариацией- моментом связи:

Если Х и У независимы, то

Часто вводят ковариацию нормированных отклонений, которую называют коэффициентом корреляции

Также важной статистической характеристикой системы является энтропия.

Энтропия - это мера неопределённости информации, она характеризует способность одной системы (источника) отдавать информацию и способность другой системы (приёмника) принимать её.

I= Hx-Hy=-Spi Logpi –(-SPjlogpj)

Важным понятием в статистике является понятие выборки. Выборка- это часть изучаемой совокупности, на основе исследования которой получают статистические закономерности, присущие всей совокупности.

Для того, чтобы полученные при исследовании выборки выводы можно было распространять на всю совокупность выборка должна быть представительной или репрезентативной, то есть правильно отражать свойства совокупности.

 

На базе статистических отображений развивается ряд математических теорий: математическая статистика, теория статистических испытаний, теория выдвижения и проверки гипотез.

 

Математическая статистика.

Математическая статистика - математическая дисциплина, которая объединяет различные методы статистического анализа, базирующиеся на использовании статистических закономерностей или их характеристик. Наиболее распространенными методами статистического анализа являются:

- регрессионный анализ (основан на сравнении математических ожиданий)

- дисперсионный анализ (основан на сравнении дисперсий)

- корреляционный анализ (учитывает математические ожидания, дисперсии и характеристики связи между событиями и процессами)

- факторный анализ (статистическая обработка многофакторного эксперимента)

- ранговая корреляция (сочетание корреляционного и факторного анализа)

При применении различных методов математической статистики статистические закономерности или их характеристики получают различными способами: путём наблюдения и исследования выборок; с помощью приближённых методов, основанных на различных способах преобразования или разбиения выборок (например, преобразование выборки в форму вариационного ряда, разбиения выборок на потоки, разряды, случайные интервалы времени).

При анализе информационных потоков и разработке систем применяются модификации и комбинации перечисленных методов.