
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методы расчета плит лежащих на упругом полупространствеСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Н.М.Герсеванову стало очевидно, что для плитных фундаментов пренебрежение распределительной способностью основания в модели Винклера приводит не только к количественным, но и качественным отличиям результатов расчета по сравнению скажем, с моделью основания в виде однородного упругого полупространства (УПП), и поэтому он инициировал и возглавил в ВИОС (НИИОСП) разработку методов расчета плит на УПП. Результаты этой работы сведены в сборник [17]. Так, в статье Н.М.Герсеванова и Я.А.Мачерета о нагруженной сосредоточенной силой бесконечно длинной балке на «упругой почве» под балкой авторы понимали балочную плиту, т.е. бесконечную и однородную в одном направлении плиту, работающую в условиях плоской деформации, а под сосредоточенной силой, соответственно, — нагрузку, распределенную с постоянной интенсивностью вдоль прямой линии того же направления. Н.М.Герсеванов и Я.А.Мачерет решают плоскую задачу теории упругости для полуплоскости, используя оригинальное представление напряжений в виде функций комплексного переменного, полученное ранее Н.М.Герсевановым. В качестве граничного условия (помимо отсутствия касательных напряжений) используется уравнение изгиба балки, связывающее перемещение границы с контактными нормальными напряжениями. Решение ищется методом функциональных уравнений и сводится к решению обыкновенного линейного дифференциального уравнения 3-го порядка. При этом очень эффективно используется герсевановское представление обобщенной δ -функции в виде предела аналитической функции [18]. Достаточно технически сложные построения позволяют представить решение в аналитической форме, доказать его корректность и выписать в конечном виде некоторые ключевые параметры, например изгибающий момент в плите в месте приложения нагрузки. Б.П.Павлов [17] решает ту же задачу несколько иными методами. У него плита задается не уравнением изгиба, а как упругая полоса конечной толщины. Используется стандартное представление решения плоской задачи теории упругости Колосова-Мусхелишвили. Задача сводится к сингулярному интегральному уравнению относительно неизвестной функции распределения контактных напряжений, которое решается методом коллокаций с использованием численного интегрирования. Из-за крайне ограниченных в то время возможностей решения систем линейных уравнений результаты получились достаточно приближенными, но качественно верными. В гипотезе упругого полупространства распределительная способность преувеличена. Модуль деформации является характеристикой, представляющей одновременно как упругие, так и остаточные деформации. При многократном приложении нагрузки остаточные деформации исчезают, модуль общей деформации E0 переходит в модуль упругости E, значительно больший, чем E0. При ширине фундамента примерно от 70 см до 7 м значение модуля деформации меняется незначительно. При превышении ширины 7 м модуль деформации заметно возрастает. Между расчетными значениями модуля деформации E0 и коэффициентом постели, исходя из приравнивания осадок, вычисленных по той и другой гипотезе, устанавливается связь:
Рис.1.4. Зависимость коэффициента k0 от отношения сторон прямоугольного фундамента α
Осадки жесткого прямоугольного фундамента на однородном основании определяются по формуле:
где P – суммарная центрированная нагрузка на фундамент. Осадки жесткой плиты лишь немного меньше (на 7%) средних осадок гибкой плиты при равномерной нагрузке. Расчеты по обеим гипотезам, даже при использовании формулы (1.1.21), дают, как правило, различные результаты в отношении изгибающих моментов в конструкции и ее изгиба. Только для узких балок при α > 10 можно подобрать отличное от определяемого формулой (1.1.21) значение коэффициента постели, при котором результаты расчета будут близки. Однако при равномерной нагрузке или при нагрузке, приближающейся к ней, получить близкие результаты расчета при любом соотношении между E0 и k невозможно. Формула соотношения между E0 и ks для узких балок шириной B имеет вид:
Гибкие фундаменты в настоящее время рассчитываются преимущественно по гипотезе упругого полупространства. Этот расчет при фундаментах большой опорной площади, в десятки или сотни квадратных метров, дает, однако, преувеличенное значение осадки, изгиба и изгибающих моментов, так как гипотеза игнорирует уплотнение грунта с глубиной, вызванного действием его собственного веса. Кроме того, при больших опорных площадях грунт под фундаментом сжимается в основном без возможности бокового расширения, что не учитывается при опытном определении модуля деформации штампом. Чтобы приблизить расчетные условия к действительным, при больших опорных площадях используют схему, согласно которой основание представляют собой сжимаемый слой, подстилаемый несжимаемым основанием.
1.7. Напряженное состояние неоднородного грунтового массива
В строительной практике часто приходится встречать грунты, неоднородные по механическим свойствам. Даже при постоянном гранулометрическом составе глубинные слои грунта имеют больший модуль деформации, чем поверхностные, в результате уплотнения весом вышележащих слоев и развития цементационных связей. Часто встречаются неоднородные напластования – грунты, подстилаемые скалой или слоем мерзлого грунта, глинистые грунты с песчаными прослойками, мерзлый грунт, подстилаемый слоем талого грунта и т.п. Наряду с неоднородностью грунтовых толщ, на распределение напряжений может влиять анизотропность грунта (неоднородность механических свойств грунта по разным направлениям). К таким грунтам относятся торфяные залежи, мерзлые грунты с ледяными прослойками, лессы, солонцеватые грунты со столбчатой структурой, ленточные глины и т.п. Рассмотрим некоторые решения для этих случаев.
где m = 1 + 1 /n – коэффициент концентрации напряжений; n – коэффициент Пуассона. Чем больше коэффициент концентрации напряжений, тем быстрее происходит затухание напряжений по мере удаления в стороны от линии действия силы.
где q – нагрузка на единицу длины загруженной линии; R – расстояние от загруженной линии до рассматриваемой точки Грунты, подстилаемые жестким слоем. Вопросу о распределении напряжений в слое грунта ограниченной толщины, залегающем на жестком несжимаемом основании, посвящено большое число работ таких ученых как К.Е.Егоров, О.Я.Шехтер, М.Н.Горбунов-Посадов и др. Близкое расположение жесткого слоя к поверхности грунта вызывает увеличение напряжений по оси действия нагрузки, т.е. происходит концентрация напряжений. Характерно, что при малых глубинах залегания жесткого слоя напряжения в грунте превышают удельное давление на штамп. М.Н.Горбуновым-Посадовым рассчитаны относительные контактные давления на поверхности (кровле) подстилающего жесткого слоя в зависимости от относительной глубины и отношения сторон подошвы штампа. Многослойные системы. Распределение напряжений в многослойных системах имеет большое значение для расчета толщины дорожных одежд, состоящих из нескольких слоев, прочность которых уменьшается с глубиной. В связи со сложностью и малой изученностью задачи о распределении напряжений в слоистых системах до сих пор большое практическое значение имеет метод эквивалентного слоя, разработанный Г.И.Покровским в 1936 г., который дает возможность при определении напряжений привести любую многослойную систему к однослойной. Идея метода заключается в том, что давление, передающееся от силы на подстилающий грунт через две плиты разной толщины и из разных материалов, будет одинаково в том случае, если равны их жесткости, т.е.
Подставив сюда моменты инерции
Следовательно, если давление на грунтовый массив передается через слой, состоящий из более жесткого материала толщиной hм, то этот слой можно мысленно заменить эквивалентным слоем самого массива грунта толщиной
Таким образом, при передаче давления на грунт через уложенный поверх него слой более жесткого материала для определения давления в подстилающем грунте верхний слой может быть заменен фиктивным эквивалентным слоем грунта такой толщины, чтобы напряжения на уровне поверхности грунтового основания оставались одинаковыми. Для дорожных одежд, работающих в стадии медленного накопления пластических деформаций, Н.Н.Иванов предложил на основании опытных данных использовать уравнение эквивалентного слоя с изменением знаком радикала и характеризовать свойства конструктивных слоев модулем деформации, а не модулем упругости:
где Е од и Е гр – модули деформации дорожной одежды и подстилающего ее грунта; Н – толщина дорожной одежды.
2. МЕТОДИКА ЭКСПЕРИМЕНТАЛЬНЫХ ИССЛЕДОВАНИЙ
|
||||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 429; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.94.208 (0.007 с.) |

 (1.1.19).
(1.1.19). Значение k0 определяется по рис. 1.1.2 в зависимости от отношения сторон прямоугольного фундамента α, его опорной площади A и коэффициента Пуассона грунта ν0, принимаемого для песков ν0 = 0.3, для суглинков и супесей ν0 = 0.35, для глин ν0 = 0.4.
Значение k0 определяется по рис. 1.1.2 в зависимости от отношения сторон прямоугольного фундамента α, его опорной площади A и коэффициента Пуассона грунта ν0, принимаемого для песков ν0 = 0.3, для суглинков и супесей ν0 = 0.35, для глин ν0 = 0.4. (1.1.20)
(1.1.20) (1.1.22).
(1.1.22). Грунт с модулем деформации, изменяющимся по глубине. Для линейно-деформируемого бесконечного полупространства, модуль которого закономерно изменяется с глубиной, при нагрузке от сосредоточенной силы применимы формулы О.К.Фрелиха:
Грунт с модулем деформации, изменяющимся по глубине. Для линейно-деформируемого бесконечного полупространства, модуль которого закономерно изменяется с глубиной, при нагрузке от сосредоточенной силы применимы формулы О.К.Фрелиха: ;
; ;
; ;
; Анизотропные грунты. В грунтовых напластованиях, модули деформации которых в горизонтальном и вертикальном направлениях различны и могут быть обозначены соответственно Е 1 и Е 2, для определения напряжений при действии линейной нагрузки можно пользоваться формулами К.Вольфа:
Анизотропные грунты. В грунтовых напластованиях, модули деформации которых в горизонтальном и вертикальном направлениях различны и могут быть обозначены соответственно Е 1 и Е 2, для определения напряжений при действии линейной нагрузки можно пользоваться формулами К.Вольфа: ;
; ;
; ,
,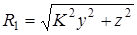 ;
;  .
. .
. , получим
, получим .
. .
. ,
,


