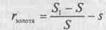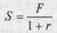Золото: паритет между форвардными и спот-ценами

Подобно тому, как арбитражные операции формируют базис между фьючерсными ценами и ценами спот на пшеницу в случае ее хранения, они определяют и разность этих цен для золота. Получаемое в результате уравнение, связывающее фьючерсные цены и цены спот, называется уравнением паритета меивду форвардными ценами и ценами спот (forward-spot price-parity relation).

Представьте себе, что вы хотите инвестировать средства в операции с золотом. Срок инвестирования составляет один год. Для этого имеется два способа. Первый состоит в покупке золота по текущей цене спот S, хранении его и продаже в конце года по цене 5 Пусть s — годовые затраты на хранение золота, выраженные в долях от цены спот. Таким образом, ваша ставка доходности составляет

 

(14.2)

 

Если, например, цена спот на золото составляет 300 долл., а затраты на хранение равны 2% годовых, ставка доходности оказывается равной

-⁼-»."

Другой способ вложения средств в золото сроком на год состоит в том, чтобы взять те же 300 долл. и вместо того, чтобы покупать золото, создать его синтетический (synthetic) аналог. Вы можете создать синтетическое золото, вложив 300 долл. (т.е. сумму, соответствующую цене спот золота) в безрисковые активы и одновременно заняв длинную позицию по форвардному контракту на золото с датой поставки через год и форвардной ценой F. Ставка доходности для такого вложения в синтетическое золото составит

Если, например, безрисковая ставка составляет 8%, ставка доходности для синтетического золота будет равна

В соответствии с законом единой цены эти два равноценных вложения средств должны давать одну и ту же доходность; вследствие этого, приравнивая друг другу выражения (14.2) и (14.3), получаем

5', -F _S-S ~~⁺''~~S~~^S

Путем несложных преобразований приходим к уравнению паритета между форвардными ценами и ценами спот на золото:

F={l+r+s)xS (14.4)

В рассматриваемом примере форвардная цена для поставки золота через год должна составить 330 долл. за унцию:

F = (1 + г + s) х S = 1,10 х 300 = 330

Если в нашем случае форвардная цена окажется выше 330 долл. за унцию, то ар-"итражеру стоит купить золото по цене спот и одновременно перепродать его для по-едующей поставки по форвардной цене. Если же, с другой стороны, форвардная Цена окажется меньше 330 долл. за унцию, то арбитражеру стоит совершить короткую "Родажу золота на спот-рынке (т.е. одолжить его и немедленно продать), вложить вырученную сумму в безрисковые активы и открыть длинную позицию по форвардному контракту.

На практике именно торговцы золотом являются теми участниками рынка, которые поддерживают паритет между форвардными ценами и ценами спот. Это связано с тем, что для них затраты на хранение и совершение сделок минимальны.

В табл. 14.2 показаны возможности ценового арбитража, которые существовали бы в случае форвардной цены, равной не 330 долл. за унцию, а 340 долл. за унцию. Торговец золотом должен был бы взять заем, использовать средства для покупки золота по цене 300 долл. за унцию и одновременно продать форвардный контракт по цене 340 долл. за унцию. После возврата займа и оплаты затрат на хранение в течение года он получит разницу в 10 долл. независимо от того, какой на этот момент окажется цена спот.

Рассмотрим теперь, какой была бы ситуация, если бы форвардная цена на золото составила только 320 долл. за унцию. В табл. 14.3 показаны возможности арбитража, которые существовали, если бы форвардная цена составляла не 330, а 320 долл. за унцию. Торговец золотом должен был бы в этом случае коротко продать на спот-рынке золото по цене 330 долл. за унцию, вложить средства в безрисковые активы и одновременно купить форвардный контракт по цене 320 долл. за унцию. После возврата займа и получения суммы, равняющейся затратам на хранение в течение года, он получит разницу в 10 долл. независимо от того, какой на этот момент окажется цена спот7.

 

Таблица 14.2. Арбитражные возможности при завышенной форвардной цене на золото-

Арбитражная позиция 1 Продажа форвардного контракта	Денежные потоки на начало го	да Денежные потоки чере 340долл -	згод S1
Заем 300 долл.	300 долл.	-324 долл.
Покупка унции золота	- 300 долл.	S1
Оплата затрат на хранение		- 6 долл.
Чистая выручка		340долл -ЗЗОдолл	= Юдолл

 

Таблица 14.3. Арбитражные возможности при заниженной форвардной цене на золото

Арбитражная позиция Денежные потоки на начало года Денежные потоки через год
Продажа на срок унции золота 300 долл. - S1
Покупка форвардного контракта 0 S1 - 320 долл.

Вложение 300 долларов в годич- - 300 долл. 324 долл.
ные бескупонные облигации

Получение затрат по хранению 6 долл.
Чистая выручка 0 330 долл.- 320 долл.=Юдолл

Уравнение паритета между форвардными ценами и ценами спот не отражает какую-либо причинно-следственную связь. Оно не утверждает, что форвардная цена определяется ценой спот и затратами на хранение. Скорее, как форвардная цена, так и цена спот задаются рынком. Если нам известна одна из них, закон единой цены дает возможность определить, какой должна быть вторая.

 

Контрольный вопрос 14.4

Предположим, что r=0,06, S=400 долл. и s=0,02. Какой должна быть форвардная цена на золото? Покажите, каким образом в случае, если она оказывается иной возникает возможность арбитража.

14.6.1. "Подразумеваемые" издержки по хранению

Одним из следствий уравнения паритета между форвардными ценами и ценами спот на золото является невозможность получить какую-либо дополнительную информацию об ожидаемой в будущем цене спот из форвардной цены помимо той, которую дает спот-рынок. В случае торговли пшеницей, описанном в разделе 14.4, мы видели, что в отсутствие зерна на хранении форвардная цена содержит такую информацию об ожидаемой в будущем цене спот, которая никак не связана с уровнем текущей цены спот. Поскольку мы рассматриваем золото, которое находится на хранении, то аналогичная информация об ожидаемых в будущем ценах не может быть получена на основании сведений о форвардной цене.

Единственная информация, которую можно извлечь из существующей цены спот и форвардной цены на золото, — это подразумеваемые издержки по хранению (implied cost of carry), которые определяются как разница между форвардной ценой и ценой спот:

Подразумеваемые издержки по хранению = F - S

Эта величина представляет собой подразумеваемые предельные издержки хранения для инвестора, которому все равно, куда вкладывать свои средства: в реальное золото или в синтетическое.

Из описываемого соотношением 14.4 уравнения паритета между форвардными ценами и ценами спот мы видим, что издержки хранения (в виде доли цены спот) складываются из безрисковой ставки доходности и складских издержек:

Таким образом, вычитая фактическую величину процентной ставки из предполагаемых издержек по хранению, можно получить размер подразумеваемых складских издержек для золота.

Предположим, например, что цена спот на золото составляет 300 долл. за унцию, форвардная цена при сроке поставки через один год равна 330 долл., а безрисковая процентная ставка составляет 8%. Чему равны подразумеваемые издержки по хранению и подразумеваемые складские издержки?

Подразумеваемые издержки по хранению = F — S = 330 долл. — 300 долл. = 30 долл. за унцию

Подразумеваемые складские издержки = (F — S)/S — г = 0,10 — 0,08 = 0,02, или 2% годовых.

Контрольный вопрос 14.5

Предположим, что цена спот на золото составляет 300 долл. за унцию, а форвардная Цена со сроком поставки через один год равна 324 долл. Чему равны подразумевае- \ мые издержки по хранению золота? Чему равны подразумеваемые складские издержки, если безрисковая ставка составляет 7% годовых?

ФИНАНСОВЫЕ ФЬЮЧЕРСЫ

рабочая книга Рассмотрим теперь вопросы ценообразования финансовых фьючерсов

;'1 Речь пойдет о поставляемых в будущем акциях, облигациях и иностран-SS J ной валюте. В отличие от таких товаров, как пшеница или золото, фи-47 нансовые активы не имеют реальной стоимости. Их не потребляют, не используют в производственных процессах, не держат ради красоты. Ценные бумаги, скорее, можно рассматривать как воплощение требований их владельцев на некие будущие доходы.

Ценные бумаги можно выпускать и хранить при очень низких затратах, что отражается в связи между их ценами слот и фьючерсными ценами. Действительно, в первом приближении мы можем полностью пренебречь этими затратами при получении уравнений паритета между форвардными ценами и ценами спот.

Рассмотрим акции гипотетического взаимного фонда S&P, портфель акций которого характеризуется широкой диверсификацией. Все дивиденды реинвестируются. Форвардный контракт на акции S&P представляет собой обещание поставить акции в некоторый определенный день по оговоренной цене поставки. Обозначим эту форвардную цену F. Сторона, открывающая длинную позицию по форвардному контракту, соглашается в день получения акций заплатить F долларов противоположной стороне, занявшей короткую позицию. Мы обозначим стоимость акции на день передачи S,.

Вместо реальной передачи акций расчеты по контракту обычно осуществляются в денежной форме. Это означает, что передачи акций не происходит, а в день платежа по контракту выплачивается только разница между F и S/. Предположим, например, что форвардная цена составляет 108 долл. за акцию. Тогда в том случае, если цена акции в день их передачи оказывается 109 долл., то сторона, занявшая длинную позицию, получает 1 долл. от стороны, занявшей короткую позицию. Однако если цена спот оказывается равной 107 долл., сторона, занявшая длинную позицию, должна выплатить 1 долл. стороне, занявшей короткую позицию.

Рассмотрим теперь связь между форвардными ценами и ценами спот для акций S&P. Предположим, что цена спот S&P составляет 100 долл., безрисковая процентная ставка равна 8% годовых, а поставка акций предусматривается через год. Какой в таком случае должна быть форвардная цена?

Отметим, что мы можем создать следующую конструкцию, по сути дублирующую получение через год акции фонда S&P. купить безрисковые бескупонные облигации номинальной стоимостью F, одновременно открыв длинную позицию по форвардному контракту для акций S&P. В срок оплаты по форвардному контракту мы погасим облигации по номинальной стоимости F и используем полученные средства для покупки акции S&P по форвардной цене.

Таким образом, форвардный контракт на акции S&P плюс бескупонная облигация образуют синтетическую акцию S&P точно с такими же характеристиками доходности, как и сами акции S&P. В соответствии с законом единой цены две эквивалентные ценные бумаги должны иметь одинаковые цены.

В табл. 14.4 показаны операции и соответствующие им выплаты, применяемые для конструирования акции с помощью бескупонных облигаций и форвардного контракта. Обратите внимание на тот факт, что акции S&P и дублирующий их портфель ценных бумаг (replicating portfolio) имеют через год одну и ту же стоимость, а именно Sj.

 

Таблица 14.4. Конструирование синтетических бездивидендных акций с помощью 'бескупонных облигаций и форвардного контракта на акции

Позиция Де» Покупка акций	южные потоки на начало года - ЮОдолл	Денежные потоки через год Si
Дублирующий портфель (синтетическая акция)
Открытие длинной позиции по форвардному контракту на акции		S,-F
Покупка бескупонных облигаций номинальной стоимостью F	-F/1,08	F
Итоговое движение денег по дублирующему портфелю	-F/1,08	Si

Приравнивая стоимость синтетической акции к стоимости реальной акции, получаем:

 

(14.5)

 

откуда следует, что цена спот равна приведенной стоимости форвардной цены, дисконтированной по безрисковой процентной ставке.

Проведя в равенстве 14.5 соответствующие преобразования, находим выражение для форвардной цены F в виде зависимости от текущего значения цены спот S и безрисковой процентной ставки г.

F = S х (1 + г) = 100 долл. х 1,08 = 108 долл.

В более общем случае, если срок выплаты по форвардному контракту и срок погашения для бескупонной облигации составляют Глет, получаем следующее уравнение паритета между форвардными ценами и ценами спот:

(14.6),

согласно которому форвардная цена равна будущей стоимости цены спот на которую начисляется сложный процент по безрисковой процентной ставке в течение Т лет.

Соблюдение этого равенства поддерживается арбитражными операциями. Для доказательства допустим, что оно не выполняется. Сначала предположим, что форвардная цена оказывается слишком высокой для данной безрисковой ставки и цены спот. Предположим, например, что г=0,08, S=100 долл. и форвардная цена, F, равна 109 долл. вместо 108 долл. Таким образом, форвардная цена оказывается на 1 долл. выше, чем та, которая следует из уравнения для паритета цен.

Наличие конкурентного рынка для акций S&P и возможности заключения форвардных контрактов на акции S&P означает также и то, что имеются возможности для арбитражных операций. Для их совершения арбитраже? должен купить акции на спот-рынке и одновременно открыть короткую позицию, продав форвардный контакт. Таким образом, он купит акции S&P, профинансировав эту покупку посредством займа на всю сумму покупки, и одновременно застрахуется от возможных потерь, открыв короткую позицию по форвардному контракту на продажу акций S&P. В результате он ничего не получит в начале года, но зато его чистая выручка в конце года ставит 1 долл. в расчете на одну акцию. Если количество акций, с которыми совершена эта операция, составляло миллион, то общий доход от арбитража будет равен 1 миллиону долл.

В табл. 14.5 проиллюстрированы операции, необходимые для такого рода арбитража. Естественно, что арбитражеры будут стараться проводить эти операции в очень больших объемах. Их деятельность на спот- и форвардных рынках ценных бумаг вызовет колебания форвардных и спот-цен до тех пор, пока равенство в уравнении 14.6 не восстановится.

 

Таблица 14.9. Арбитражные операции с фьючерсными контрактами на акции

Арбитражная позиция	Денежные потоки на начало года	Денежные потоки через год
Продажа форвардного контракта		109долл -Si
Заем ЮОдолл	100 долл.	- 108 долл.
Покупка акций	-ЮОдолл	S)
Чистая выручка		1 долл

 

Как мы уже раньше видели, анализируя операции с золотом, из уравнения паритета между форвардными ценами и ценами спот не следуют какие-либо конкретные рекомендации. Это уравнение не позволяет определить форвардную цену на основе цен спот и безрисковой ставки доходности. Все три входящих в него переменных — F, S и г— задаются рынком. Если мы знаем любые две из этих величин, то в соответствии с законом единой цены можем определить, чему должна равняться третья.

14.8. "ПОДРАЗУМЕВАЕМАЯ" БЕЗРИСКОВАЯ СТАВКА ДОХОДНОСТИ

Подобно тому, как можно сконструировать синтетические акции, воспользовавшись безрисковыми активами и форвардным контрактом на акции, можно синтезировать и безрисковую бескупонную облигацию, купив акции и одновременно открыв короткую позицию по форвардному контракту. Предположим, что F равно 108 долл., Сравняется 108 долл., а Г составляет один год. Мы можем сконструировать синтетическую годичную бескупонную облигацию номинальной стоимостью 108 долл., купив акции по 100 долл. и одновременно открыв короткую позицию по поставке через год акций по форвардной цене 108 долл

Первоначальные расходы составляют 100 долл., а выручка через год составит 108 долл. независимо от того, какой окажется цена спот (S,) для акций. Таким образом, если вы можете купить синтетическую годичную бескупонную облигацию (или казначейский вексель) номинальной стоимостью 108 долл. за полную стоимость в 100 долл., подразумеваемая безрисковая ставка составляет 8%. Совершаемые при этом операции проиллюстрированы в табл. 14.6.

В более общей форме подразумеваемая безрисковая ставка доходности, которую можно получить посредством покупки акций и открытия короткой позиции по форвардному контракту, равна

 

(14.7)

 

Таблица 14.6. Конструирование синтетической бескупонной облигации с помощью акций и форвардного контракта

Позиция Денежные потоки на Денежные потоки че-начало года рез год

Покупка казначейского векселя номиналом 108 долл. -108 долл /(1 +г) 108 долл. Дублирующий портфель ценных бумаг (синтетический казначейский вексель) Покупка акций -ЮОдолл 81 Открытие короткой позиции 0 (108 - S1) долл. Итоговые движения денег по дублирующему портфелю -ЮОдолл 108 долл