Формирование наиболее предпочтительного инвестиционного портфеля

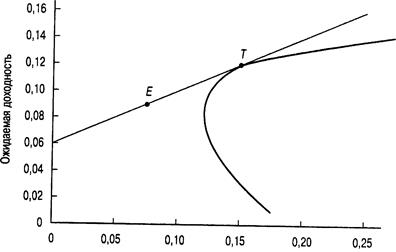
Чтобы завершить анализ, давайте рассмотрим выбор инвестора с точки зрения его предпочтений и с учетом графика соотношения риск/доходность для эффективных портфелей. Надеюсь, вы не забыли, что в разделе 12.1 мы упоминали о том, что предпочтения при формировании портфеля зависят от стадии жизненного цикла, на которой находится инвестор, периода (горизонта) планирования и толерантности к риску. Следовательно, инвестор может выбрать позицию в любой точке на отрезке, ограниченном точками F и Г. На рис. 12.5 для этого выбрана точка Е. Портфель, который соответствует точке Е, на 50% состоит из портфельных инвестиций в общей точке (тангенциальный портфель) и на 50% из инвестиций в безрисковый актив. Преобразуем уравнения 12.1 и 12.2 таким образом, чтобы они отражали тот факт, что портфель в точке касания — это теперь единственный рискованный актив, который следует объединять с безрисковым активом. Выясняется, что ожидаемая доходность и стандартное отклонение портфеля Е имеют вид:

() = /у + 0,5 х [£(/y) - /7] = 0,06 + 0,5(0,122 - 0,06) = 0,091 ст= 0,5ха,- =0,5х0,146=0.073

Учитывая, что тангенциальный портфель состоит на 69,2% из рискованного актива 1 и на 30,8% — из рискованного актива 2, можно определить, что состав портфеля будет следующим:

Доля безрискового актива		50,0%
Доля рискованного актива 1	0,5х69,2%=	34,6%
Доля рискованного актива 2	0,5х30,8%=	15,4%
Всего		100,0%

 

Следовательно, если вы инвестировали 100000 долл. в портфель Е, то 50000 долл. инвестировано в безрисковый актив, 34600 долл. — в рискованный актив 1 15400 долл. — в рискованный актив 2.

Давайте теперь обобщим имеющиеся у нас сведения относительно создания эффективного портфеля, когда имеется два вида рискованных активов и один безрисковый актив. Существует только один портфель с рискованными активами, который оптимальным образом можно объединить с безрисковым активом. Мы называем этот особенный портфель с рискованными активами, соответствующий общей (тангенциальной) точке Г на рис. 12.4, оптимальной комбинацией рискованных активов. Предпочтительный портфель всегда является какой-либо комбинацией портфеля рискованных активов в общей точке и безрискового актива.

Стандартное отклонение Рис. 12.5. Выбор наиболее предпочтительного портфеля

12.3.4. Как получить заданную ожидаемую доходность: пример 2

Предположим, что у вас имеется 100000 долл., которые вы хотели бы инвестировать с ожидаемой ставкой доходности в 0,10 годовых. Сравните стандартное отклонение доходности, на которое вам пришлось бы пойти при прежнем графике риск/доходность (линия, соединяющая точки Ей S) со стандартным отклонением при новом графике риск/доходность (линия, соединяющая точки F и 7). Каков состав каждого из этих двух портфелей?

Решение

Во-первых, давайте запишем формулу, связывающую ожидаемую доходность Портфеля с долей, инвестированной в рискованные активы, и решим его. Таким обра-эом мы определим долю, которую надо инвестировать в рискованные активы. Для но-"ого соотношения риск/доходность, в котором используется оптимальная комбинация Двух рискованных активов, формула имеет следующий вид:

£ (г) =£•(/,>+г, (1-w) £(/•)= 0,122w+0,06(1-н')

 

Установив ожидаемую ставку доходности портфеля равной 0,10 и определив н', получим:

£(/-)=-0,06 + 0,062w =0,10

0,10-0,06..-

w = ————— = 0,6D 0,062

Следовательно, для получения оптимальной комбинации 65% от 100000 долл. должно быть инвестировано в рискованные активы, а 35% — в безрисковый актив. Стандартное отклонение в таком портфеле определяется по формуле:

(j=\v(t =0,65х0,146=0,095

Поскольку оптимальная комбинация рискованных активов сама по себе содержит 69,2% рискованного актива 1 и 30,8% рискованного актива 2, состав итогового портфеля с ожидаемой доходностью в 0,10 в год определяется следующим образом:

Доля безрискового актива		35%
Доля рискованного актива 1	0,65х69,2%=	45%
Доля рискованного актива 2	0,65х30,8%=	20%
Всего		100%

Для прежнего графика соотношения риск/доходность с единственным рискованным активом формула, связывающая ожидаемую доходность и w, имела вид:

£(r) =£(/•>+/у (1-uQ £(r)=0,14w+0,06(l-w)

Установив ожидаемую ставку доходности портфеля равной 0,10 и вычислив w, получим:

£(r)= 0,06+0,08=0,10

	0,10	-0,		-0,
w =	0,

Таким образом, 50% от 100000 долл. должно быть вложено в рискованный актив 1.

а 50% — в безрисковый актив.

Стандартное отклонение этого портфеля задано уравнением:

 

Контрольный вопрос 12.9

Предположим, инвестор выбрал портфель, который на рис. 12.5 соответствует точке, лежащей на отрезке между точками F и Т на расстоянии в три четверти длины отрезка от точки F. Другими словами, 75% его портфеля вложено в портфель, соответствующий общей точке, а 25% — в безрисковый актив. Какова ожидаемая ставка доходности и стандартное отклонение этого портфеля? Если у инвестора имеете 1000000 долл., то сколько ему следует вложить в каждый из трех активов?

 

Важно отметить, что при поиске оптимальной комбинации рискованных активов нам не нужно ничего знать ни о благосостоянии инвестора, ни о его предпочтениях. Состав этого портфеля зависит только от ожидаемых ставок доходности и стандартных отклонений рискованного актива 1 и рискованного актива 2 и от корреляции между ними. Это означает, что все инвесторы, которые согласились на такие характеристики доходности (среднее значение, стандартное отклонение, корреляция), захотят инвестировать в один и тот же тангенциальный портфель, дополненный безрисковым активом. Вот общее правило, применимое ко всем случаям, когда имеется множество рискованных активов:

Всегда существует оптимальный портфель рискованных активов, который все инвесторы, избегающие риска и имеющие одинаковые представления о характеристиках

доходности, будут объединять с безрисковым активом с целью получения наиболее предпочтительного портфеля.