

Мы поможем в написании ваших работ!
ЗНАЕТЕ ЛИ ВЫ?
|
Повторення курсу « ГЕОМЕТРІЯ-10»
| Планіметрія
Л.Я. Федченко, Донецьк, „Каштан”, 2009. Збірник завдань для тематичних і підсумкових атестацій. Геометрія 7-9 класи.
| | Тема: Прямокутний трикутник
| | Розділ
| І рівень
| ІІ рівень
| ІІІ рівень
| | Теорема Піфагора
| № 955-956;
№ 969-974;
№ 983-994;
№ 997-1022
| № 1277-1281;
№ 1283;
№1285-1288;
№ 1291-1294;
№ 1304; № 1307;
№1309, № 1310;
№ 1331-1336;
№ 1338-1340
| № 1556-1571;
№ 1574;
№ 1575;
№ 1577;
№ 1580;
№ 1585;
№ 1594
| | Співвідношення між сторонами та кутами прямокутного трикутника
| № 953; № 954; №967; № 968; № 975-978;
№ 995; № 996;
№ 1010;
№1018-1021;
№ 1024-1030
| № 1275-1278;
№ 1305;
№ 1311-1315;
№ 1317;
№ 1318-1340
| № 1554;
№ 1555;
№ 1578-1584;
№ 1586;
№ 1587;
№ 1590;
№ 1591;
№ 1595;
№ 1596;
№ 1602;
№ 1603;
№ 1608-1615
| | Теорема синусів
| № 1663-1667
| № 1940-1945
| № 2101;
№ 2102
| | Теорема косинусів
| № 1650-1657
| № 1924-1931
| № 2093-2096
| | Координати на площині
| № 1766-1790
| № 2002-2005
| № 2148-2153
| | Вектори на площині
| № 1841-1887
| № 2047-2073
| № 2197-2222
| | Стереометрія
Г.М. Литвиненко, Л.Я Федченко, В.А.Швець, Донецьк, 2000. Збірник завдань для екзамену з математики на атестат про середню освіту. Геометрія 10-11.
| | Тема: Паралельність у просторі
| | Розділ
| І рівень
| ІІ рівень
| ІІІ рівень
| | Паралельність прямих
| № 1а; № 6;
№ 9
| № 47; № 63;
№ 73; № 75
|
| | Паралельність прямої та площини
| № 15; № 19;
№ 27; № 35
| № 46; № 67;
№ 70; № 71
| № 119;
№ 120
| | Паралельність площин
| № 8; № 10;
№ 12; № 17
| № 49; № 50;
№ 52; № 74
| № 180
| | Комбіновані задачі
| № 11; № 7;
№ 13;
№ 14; № 40
| № 41; № 42;
№ 43; № 44; № 45
|
| | Тема: Перпендикулярність у просторі
| | Перпендикулярність прямих
|
№ 20; № 21
|
№ 68; № 69
|
| | Теорема про три перпендикуляри
| № 23
| № 57; №77;
№ 93; № 96
|
| | Перпендикулярність прямої і площини
|
№ 18; № 22;
№ 25; № 36
| № 48; № 53; № 54;
№ 72; № 85; № 86;
№ 89; № 91; № 92
|
№ 148; № 172
| | Перпендикулярність площин
|
№ 26
| № 58; № 60; №80;
№ 110; № 111; №112; №113
|
№ 135; № 154
| | Комбіновані задачі
| № 28
| № 51
| №121; №130; №131; №132; № 133
| | Тема: Відстані і кути у просторі
| | Відстані між прямими
|
|
| № 137; №175
| | Відстань від точки до площини
|
| № 79; № 81; № 88;
№ 106; № 107;
№ 108; № 109;
№ 115; № 116
| № 151; № 152;
№ 168; № 169;
№ 176; № 177
| | Відстань між площинами
|
|
| № 163
| | Кут між прямою і площиною
| № 29; № 34
| № 65; № 78
| № 123;
№ 165;
№ 173;
№ 178
| | Кут між площинами
| № 24; № 30
| № 61; № 100;
№ 102; № 117;
№ 118
| № 124; № 126;
№ 149; № 150;
№ 153; № 157
№ 160; № 164;
№ 171; № 182;
№ 183; № 184
| | Відстань від точки до вершин многокутника
| № 32
| № 59; № 76; № 82; № 83; № 97; № 104; № 105
| № 129; № 134;
№ 139; № 147;
№ 159; № 166
| | Відстань від точки до сторін многокутника
| № 31
| № 55; № 56; № 84; №87; № 90; № 94; № 95; № 98; № 101; № 103; № 114
| № 127; № 136; № 138; № 155; № 158; № 162; № 167;
№ 170; № 179;
| | Комбіновані задачі
| № 33
| № 64; № 66
| № 122; № 125; № 128; № 140; № 161; № 181; № 185
| | | | | | | | | | Урок №1. Система опорних фактів з планіметрії. Координати та вектори на площині.
Індивідуальна робота з теми «Вектори»
Дано точки А, В, С, D.
1. Знайдіть координати векторів 
2. Знайдіть абсолютну величину векторів 
3. Знайдіть скалярні добутки: 
4. Визначите вид кута між векторами  й й  і вид кута, утвореного векторами і вид кута, утвореного векторами  й й  . .
5. Знайдіть значення косинуса кута між векторами  й й  і векторами і векторами  и. и. 
6. Знайдіть координати точок Р и К, якщо Р - середина відрізка ВР, а К - середина відрізка DС.
7. Знайдіть довжину відрізка РК.
8. Знайдіть координати векторів  й й  . .
9. З'ясувати, чи будуть вектори 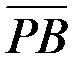 й й  перпендикулярними? перпендикулярними?
10. Встановити, чи є вектори  й й  колінеарними? колінеарними?
11. Встановити вид чотирикутника АВСD.
12. Встановити вид трикутника РСК.
13. Відкласти від точки D вектор, який дорівнює вектору  . .
14. Відкласти від початку координат вектор  , заданий формулою , заданий формулою  (двома способами). (двома способами).
15. Відкласти від початку координат вектор  , заданий формулою , заданий формулою  (двома способами). (двома способами).
16. Виразити вектор  через вектори через вектори  й й  , де Р и К - середини сторін ВР і DС відповідно. , де Р и К - середини сторін ВР і DС відповідно.
17. Складіть рівняння окружності, діаметром якої є відрізок ВР.
18. Складіть рівняння прямої РК.
Варіанти завдань
| 1.А(-3; 5) В(- 3; 8) С(2;10) D(2; 7)
| 14.А(2;3) В(3;5) С(10;1) D(11;-2)
| 27.А(-2;-2) В(-4;-6) С(4;-10) D(6;-6)
| | 2.А(- 9; 1) В(- 7; 5) С(-3;7) D(-5; 3)
| 15.А(7;-1) В(4;-4)
С(-2;-6) D(1;-3)
| 28.А(-8;-2) В(-10;1)
С(-4;5) D(1;4)
| | 3.А(0; 0) В(0; 2)
С(6;8) D(10; 10)
| 16.А(-7;-2) В(-1;-3) С(0;-10) D(-7;-9)
| 29.А(-6;-1) В(0;1) С(6;1) D(0;-1)
| | 4.А(-2;1) В(-1;6) С(-6;7) D(-7;2)
| 17.А(-9;4) В(-8;7)
С(-5;9) D(0;10)
| 30.А(0;0) В(4;-1) С(5;-5) D(1;-4)
| | 5.А(-2;-2) В(0;2) С(6;8) D(10;10)
| 18.А(4;-1) В(7;-4) С(4;-7) D(1;-4)
| 31.А(-7;4) В(-3;2)
С(-1;-2) D(-3;-4)
| | 6.А(2;3) В(3;5) С(10;1) D(9;-1)
| 19.А(9;-4) В(11;2) С(12;2) D(14;-4)
| 32.А(-2;0) В(-1;4) С(3;3) D(2;-1)
| | 7.А(-3;1) В(-1;7) С(2;6) D(-1;-3)
| 20.А(-8;-2) В(-10;1) С(-1;7) D(1;4)
| 33.А(-3;-2) В(-4;4) С(4;-4) D(-2;-3)
| | 8.А(-14;-2) В(-11;2) С(-3;2) D(-6;-2)
| 21.А(-4;-6) В(-2;-2) С(2;-4) D(4;-10)
| 34.А(-2;-1) В(-2;-2) С(7;-2) D(7;-1)
| | 9.А(6;0) В(5;-5) С(0;-6) D(1;-1)
| 22.А(0;6) В(5;4) С(7;0) D(2;2)
| 35.А(-2;-1) В(-2;-2) С(7;-2) D(3;-1)
| | 10.А(-4;-10) В(0;-6) С(4;-6) D(2;-10)
| 23.А(0;2) В(1;5) С(0;8) D(-1;5)
| 36.А(0;-6) В(4;-4)
С(4;-8) D(0;-10)
| | 11.А(-5;-1) В(-2;-3)
С(-4;-6) D(-7;-4)
| 24.А(0;2) В(0;6) С(3;9) D(6;8)
| 37.А(7;0) В(10;2) С(13;0) D(10;-2)
| | 12.А(-4;-10) В(0;-6) С(4;-6) D(8;-10)
| 25.А(3;0) В(1;3) С(7;2) D(6;-1)
| 38.А(4;-4) В(5;0) С(8;0) D(13;-4)
| | 13.А(-3;1) В(-1;7)
С(2;6) D(0;0)
| 26.А(0;2) В(0;6) С(3;9) D(7;9)
| | Математичний диктант №1
Варіант 1
1.Запишіть коротко «вектор а».
2. Зобразити вектор  .
3.Запишіть позначення вектора з кінцем у точці Х та початком у точці У.
4.Зобразити два однаково спрямованих, але не рівних вектора.
5.Що можна сказати про напрямок двох рівних векторів?
6.Запишіть у вигляді рівності, чому дорівнює абсолютна величина нульового вектора.
7. Зобразити вектор .
3.Запишіть позначення вектора з кінцем у точці Х та початком у точці У.
4.Зобразити два однаково спрямованих, але не рівних вектора.
5.Що можна сказати про напрямок двох рівних векторів?
6.Запишіть у вигляді рівності, чому дорівнює абсолютна величина нульового вектора.
7. Зобразити вектор  і точку У. Відкладіть від точки У вектор, рівний і точку У. Відкладіть від точки У вектор, рівний  .
8. Запишіть за допомогою позначень «довжина вектора .
8. Запишіть за допомогою позначень «довжина вектора  дорівнює 3 см».
9.Знайдіть довжину вектора, зображеного на рисунку:
Т
3 см
S 5 см
10. Чи вірно твердження: «Якщо вектори дорівнює 3 см».
9.Знайдіть довжину вектора, зображеного на рисунку:
Т
3 см
S 5 см
10. Чи вірно твердження: «Якщо вектори  й й  рівні, то вони колінеарні»? рівні, то вони колінеарні»?
| Математичний диктант №1
Варіант 2
1.Запишіть коротко «вектор в».
2. Зобразити вектор 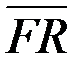 .
3.Запишіть позначення вектора з кінцем у точці Р та початком у точці А.
4.Запишіть у вигляді рівності, чому дорівнює абсолютна величина нульового вектора.
5. Зобразити вектор .
3.Запишіть позначення вектора з кінцем у точці Р та початком у точці А.
4.Запишіть у вигляді рівності, чому дорівнює абсолютна величина нульового вектора.
5. Зобразити вектор  і точку М. Відкладіть від точки М вектор, який дорівнює вектору і точку М. Відкладіть від точки М вектор, який дорівнює вектору  .
6.Що можна сказати про напрямок двох рівних векторів?
7.Зобразити два однаково спрямованих, але не рівних вектора.
8. Запишіть за допомогою позначень «довжина вектора .
6.Що можна сказати про напрямок двох рівних векторів?
7.Зобразити два однаково спрямованих, але не рівних вектора.
8. Запишіть за допомогою позначень «довжина вектора 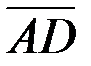 дорівнює 4 см».
9.Знайдіть довжину вектора, зображеного на малюнку:
М
К 2 см
6 см
10. Чи вірно твердження: «Якщо два вектори колінеарні, то вони однаково спрямовані»? дорівнює 4 см».
9.Знайдіть довжину вектора, зображеного на малюнку:
М
К 2 см
6 см
10. Чи вірно твердження: «Якщо два вектори колінеарні, то вони однаково спрямовані»?
| Математичний диктант №2
Варіант 1
1. Знайдіть координати вектора  , де А(1;3), В(-2;0).
2. Знайдіть довжину вектора , де А(1;3), В(-2;0).
2. Знайдіть довжину вектора
 (-3;4).
3. Знайдіть суму векторів (-3;4).
3. Знайдіть суму векторів  (-3;2) і (-3;2) і  (-4;5).
4. Чи колінеарні вектори (-4;5).
4. Чи колінеарні вектори  (-1;2) і (-1;2) і  (2;-4)?
5. Знайдіть скалярний добуток векторів (2;-4)?
5. Знайдіть скалярний добуток векторів  (1;5) і (1;5) і  (-3;-2).
6. Знайдіть скалярний добуток векторів (-3;-2).
6. Знайдіть скалярний добуток векторів  й й  , якщо , якщо 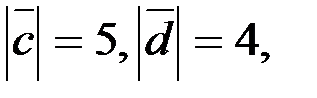 а кут між цими векторами дорівнює 300.
7. Чи перпендикулярні вектори а кут між цими векторами дорівнює 300.
7. Чи перпендикулярні вектори
 (-2;3) і (-2;3) і  (-1;2)?
8. Знайдіть кут між векторами (-1;2)?
8. Знайдіть кут між векторами  (1;1) і (1;1) і  (1;0).
9. Знайдіть косинус кута між векторами (1;0).
9. Знайдіть косинус кута між векторами  (-3;1) і (-3;1) і  (3;-4).
10. Вектор (3;-4).
10. Вектор  має координати (-3;8), а точка F(5;2). Знайдіть координати точки К. має координати (-3;8), а точка F(5;2). Знайдіть координати точки К.
| Математичний диктант №2
Варіант 2
1. Знайдіть координати вектора  , де А(2;4), В(-3;0).
2. Знайдіть довжину вектора , де А(2;4), В(-3;0).
2. Знайдіть довжину вектора
 (6;-8).
3. Знайдіть суму векторів (6;-8).
3. Знайдіть суму векторів  (-2;3) і (-2;3) і  (-4;7).
4. Чи колінеарні вектори (-4;7).
4. Чи колінеарні вектори  (-2;4) і (-2;4) і  (6;-5)?
5. Знайдіть скалярний добуток векторів (6;-5)?
5. Знайдіть скалярний добуток векторів  (3;4) і (3;4) і  (-2;1).
6. Знайдіть скалярний добуток векторів (-2;1).
6. Знайдіть скалярний добуток векторів  й й  , якщо , якщо  а кут між цими векторами дорівнює 450.
7. Чи перпендикулярні вектори а кут між цими векторами дорівнює 450.
7. Чи перпендикулярні вектори  (-3;2) і (-3;2) і  (4;6)?
8. Знайдіть кут між векторами (4;6)?
8. Знайдіть кут між векторами  (2;2) і (2;2) і  (0;2).
9. Знайдіть косинус кута між векторами (0;2).
9. Знайдіть косинус кута між векторами  (-2;1) і (-2;1) і  (4;-3).
10. Вектор (4;-3).
10. Вектор  має координати (-4;-3), а точка F(1;3). Знайдіть координати точки К. має координати (-4;-3), а точка F(1;3). Знайдіть координати точки К.
| Варіант 3
1. Знайдіть координати вектора  , де А(3;5), В(-3;2).
2. Знайдіть довжину вектора , де А(3;5), В(-3;2).
2. Знайдіть довжину вектора
 (2;-4).
3. Знайдіть суму векторів (2;-4).
3. Знайдіть суму векторів  (-4;2) і (-4;2) і  (5;7).
4. Чи колінеарні вектори (5;7).
4. Чи колінеарні вектори  (8;-4) і (8;-4) і  (-2;-1)?
5.Знайдіть скалярний добуток векторів (-2;-1)?
5.Знайдіть скалярний добуток векторів  (4;2) і (4;2) і  (-2;1).
6. Знайдіть скалярний добуток векторів (-2;1).
6. Знайдіть скалярний добуток векторів  й й  , якщо , якщо  а кут між цими векторами дорівнює 1500.
7. Чи перпендикулярні вектори а кут між цими векторами дорівнює 1500.
7. Чи перпендикулярні вектори 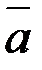 (3;2) і (3;2) і  (-4;6)?
8. Знайдіть кут між векторами (-4;6)?
8. Знайдіть кут між векторами
 (-1;1) і (-1;1) і  (-1;0).
9.Знайдіть косинус кута між векторами (-1;0).
9.Знайдіть косинус кута між векторами  (3;1) і (3;1) і  (3;4).
10. Вектор (3;4).
10. Вектор  має координати (2;11), а точка F(2;-3). Знайдіть координати точки К. має координати (2;11), а точка F(2;-3). Знайдіть координати точки К.
| Варіант 4
1. Знайдіть координати вектора  , де А(4;6), В(-2;4).
2. Знайдіть довжину вектора , де А(4;6), В(-2;4).
2. Знайдіть довжину вектора
 (-8;2).
3. Знайдіть суму векторів (-8;2).
3. Знайдіть суму векторів  (2;-6) і (2;-6) і  (4;-8).
4. Чи колінеарні вектори (4;-8).
4. Чи колінеарні вектори  (7;-3) і (7;-3) і  (1;-4)?
5.Знайдіть скалярний добуток векторів (1;-4)?
5.Знайдіть скалярний добуток векторів  (3;2) і (3;2) і  (-4;6).
6. Знайдіть скалярний добуток векторів (-4;6).
6. Знайдіть скалярний добуток векторів  й й  , якщо , якщо  а кут між цими векторами дорівнює 1350.
7. Чи перпендикулярні вектори а кут між цими векторами дорівнює 1350.
7. Чи перпендикулярні вектори  (4;2) і (4;2) і  (-2;1)?
8. Знайдіть кут між векторами (-2;1)?
8. Знайдіть кут між векторами
 (-2;2) і (-2;2) і  (0;-2).
9.Знайдіть косинус кута між векторами (0;-2).
9.Знайдіть косинус кута між векторами  (2;1) і (2;1) і  (4;3).
10. Вектор (4;3).
10. Вектор  має координати (-9;10), а точки F(4;-3). Знайдіть координати точки К. має координати (-9;10), а точки F(4;-3). Знайдіть координати точки К.
|
|






 й
й  і вид кута, утвореного векторами
і вид кута, утвореного векторами  й
й  .
. й
й  і векторами
і векторами  и.
и. 
 й
й  .
.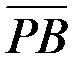 й
й  перпендикулярними?
перпендикулярними? й
й  колінеарними?
колінеарними? .
. , заданий формулою
, заданий формулою  (двома способами).
(двома способами). , заданий формулою
, заданий формулою  (двома способами).
(двома способами). через вектори
через вектори  й
й  , де Р и К - середини сторін ВР і DС відповідно.
, де Р и К - середини сторін ВР і DС відповідно. .
3.Запишіть позначення вектора з кінцем у точці Х та початком у точці У.
4.Зобразити два однаково спрямованих, але не рівних вектора.
5.Що можна сказати про напрямок двох рівних векторів?
6.Запишіть у вигляді рівності, чому дорівнює абсолютна величина нульового вектора.
7. Зобразити вектор
.
3.Запишіть позначення вектора з кінцем у точці Х та початком у точці У.
4.Зобразити два однаково спрямованих, але не рівних вектора.
5.Що можна сказати про напрямок двох рівних векторів?
6.Запишіть у вигляді рівності, чому дорівнює абсолютна величина нульового вектора.
7. Зобразити вектор  і точку У. Відкладіть від точки У вектор, рівний
і точку У. Відкладіть від точки У вектор, рівний  .
8. Запишіть за допомогою позначень «довжина вектора
.
8. Запишіть за допомогою позначень «довжина вектора  дорівнює 3 см».
9.Знайдіть довжину вектора, зображеного на рисунку:
Т
3 см
S 5 см
10. Чи вірно твердження: «Якщо вектори
дорівнює 3 см».
9.Знайдіть довжину вектора, зображеного на рисунку:
Т
3 см
S 5 см
10. Чи вірно твердження: «Якщо вектори  й
й  рівні, то вони колінеарні»?
рівні, то вони колінеарні»?
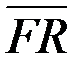 .
3.Запишіть позначення вектора з кінцем у точці Р та початком у точці А.
4.Запишіть у вигляді рівності, чому дорівнює абсолютна величина нульового вектора.
5. Зобразити вектор
.
3.Запишіть позначення вектора з кінцем у точці Р та початком у точці А.
4.Запишіть у вигляді рівності, чому дорівнює абсолютна величина нульового вектора.
5. Зобразити вектор  і точку М. Відкладіть від точки М вектор, який дорівнює вектору
і точку М. Відкладіть від точки М вектор, який дорівнює вектору  .
6.Що можна сказати про напрямок двох рівних векторів?
7.Зобразити два однаково спрямованих, але не рівних вектора.
8. Запишіть за допомогою позначень «довжина вектора
.
6.Що можна сказати про напрямок двох рівних векторів?
7.Зобразити два однаково спрямованих, але не рівних вектора.
8. Запишіть за допомогою позначень «довжина вектора 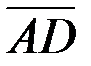 дорівнює 4 см».
9.Знайдіть довжину вектора, зображеного на малюнку:
М
К 2 см
6 см
10. Чи вірно твердження: «Якщо два вектори колінеарні, то вони однаково спрямовані»?
дорівнює 4 см».
9.Знайдіть довжину вектора, зображеного на малюнку:
М
К 2 см
6 см
10. Чи вірно твердження: «Якщо два вектори колінеарні, то вони однаково спрямовані»?
 , де А(1;3), В(-2;0).
2. Знайдіть довжину вектора
, де А(1;3), В(-2;0).
2. Знайдіть довжину вектора
 (-3;4).
3. Знайдіть суму векторів
(-3;4).
3. Знайдіть суму векторів  (-3;2) і
(-3;2) і  (-4;5).
4. Чи колінеарні вектори
(-4;5).
4. Чи колінеарні вектори  (-1;2) і
(-1;2) і  (2;-4)?
5. Знайдіть скалярний добуток векторів
(2;-4)?
5. Знайдіть скалярний добуток векторів  (1;5) і
(1;5) і  (-3;-2).
6. Знайдіть скалярний добуток векторів
(-3;-2).
6. Знайдіть скалярний добуток векторів  й
й  , якщо
, якщо 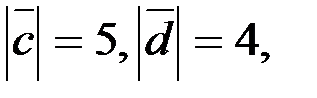 а кут між цими векторами дорівнює 300.
7. Чи перпендикулярні вектори
а кут між цими векторами дорівнює 300.
7. Чи перпендикулярні вектори
 (-2;3) і
(-2;3) і  (-1;2)?
8. Знайдіть кут між векторами
(-1;2)?
8. Знайдіть кут між векторами  (1;1) і
(1;1) і  (1;0).
9. Знайдіть косинус кута між векторами
(1;0).
9. Знайдіть косинус кута між векторами  (-3;1) і
(-3;1) і  (3;-4).
10. Вектор
(3;-4).
10. Вектор  має координати (-3;8), а точка F(5;2). Знайдіть координати точки К.
має координати (-3;8), а точка F(5;2). Знайдіть координати точки К.
 , де А(2;4), В(-3;0).
2. Знайдіть довжину вектора
, де А(2;4), В(-3;0).
2. Знайдіть довжину вектора
 (6;-8).
3. Знайдіть суму векторів
(6;-8).
3. Знайдіть суму векторів  (-4;7).
4. Чи колінеарні вектори
(-4;7).
4. Чи колінеарні вектори  (-2;4) і
(-2;4) і  (6;-5)?
5. Знайдіть скалярний добуток векторів
(6;-5)?
5. Знайдіть скалярний добуток векторів  (3;4) і
(3;4) і  (-2;1).
6. Знайдіть скалярний добуток векторів
(-2;1).
6. Знайдіть скалярний добуток векторів  й
й  , якщо
, якщо  а кут між цими векторами дорівнює 450.
7. Чи перпендикулярні вектори
а кут між цими векторами дорівнює 450.
7. Чи перпендикулярні вектори  (-3;2) і
(-3;2) і  (4;6)?
8. Знайдіть кут між векторами
(4;6)?
8. Знайдіть кут між векторами  (2;2) і
(2;2) і  (0;2).
9. Знайдіть косинус кута між векторами
(0;2).
9. Знайдіть косинус кута між векторами  (-2;1) і
(-2;1) і  (4;-3).
10. Вектор
(4;-3).
10. Вектор  має координати (-4;-3), а точка F(1;3). Знайдіть координати точки К.
має координати (-4;-3), а точка F(1;3). Знайдіть координати точки К.
 , де А(3;5), В(-3;2).
2. Знайдіть довжину вектора
, де А(3;5), В(-3;2).
2. Знайдіть довжину вектора
 (2;-4).
3. Знайдіть суму векторів
(2;-4).
3. Знайдіть суму векторів  (-4;2) і
(-4;2) і  (5;7).
4. Чи колінеарні вектори
(5;7).
4. Чи колінеарні вектори  (8;-4) і
(8;-4) і  (-2;-1)?
5.Знайдіть скалярний добуток векторів
(-2;-1)?
5.Знайдіть скалярний добуток векторів  (4;2) і
(4;2) і  (-2;1).
6. Знайдіть скалярний добуток векторів
(-2;1).
6. Знайдіть скалярний добуток векторів  й
й  , якщо
, якщо  а кут між цими векторами дорівнює 1500.
7. Чи перпендикулярні вектори
а кут між цими векторами дорівнює 1500.
7. Чи перпендикулярні вектори 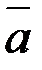 (3;2) і
(3;2) і  (-4;6)?
8. Знайдіть кут між векторами
(-4;6)?
8. Знайдіть кут між векторами
 (-1;1) і
(-1;1) і  (-1;0).
9.Знайдіть косинус кута між векторами
(-1;0).
9.Знайдіть косинус кута між векторами  (3;1) і
(3;1) і  (3;4).
10. Вектор
(3;4).
10. Вектор  має координати (2;11), а точка F(2;-3). Знайдіть координати точки К.
має координати (2;11), а точка F(2;-3). Знайдіть координати точки К.
 , де А(4;6), В(-2;4).
2. Знайдіть довжину вектора
, де А(4;6), В(-2;4).
2. Знайдіть довжину вектора
 (-8;2).
3. Знайдіть суму векторів
(-8;2).
3. Знайдіть суму векторів  (2;-6) і
(2;-6) і  (4;-8).
4. Чи колінеарні вектори
(4;-8).
4. Чи колінеарні вектори  (7;-3) і
(7;-3) і  (1;-4)?
5.Знайдіть скалярний добуток векторів
(1;-4)?
5.Знайдіть скалярний добуток векторів  (3;2) і
(3;2) і  (-4;6).
6. Знайдіть скалярний добуток векторів
(-4;6).
6. Знайдіть скалярний добуток векторів  й
й  , якщо
, якщо  а кут між цими векторами дорівнює 1350.
7. Чи перпендикулярні вектори
а кут між цими векторами дорівнює 1350.
7. Чи перпендикулярні вектори  (4;2) і
(4;2) і  (-2;1)?
8. Знайдіть кут між векторами
(-2;1)?
8. Знайдіть кут між векторами
 (-2;2) і
(-2;2) і  (0;-2).
9.Знайдіть косинус кута між векторами
(0;-2).
9.Знайдіть косинус кута між векторами  (2;1) і
(2;1) і  (4;3).
10. Вектор
(4;3).
10. Вектор  має координати (-9;10), а точки F(4;-3). Знайдіть координати точки К.
має координати (-9;10), а точки F(4;-3). Знайдіть координати точки К.



