ЗМІСТ
| 1.
| Календарно – тематичне планування
|
|
| 2.
| Довідковий матеріал з теми
|
|
| 3.
| Довідковий матеріал з повторення
|
|
| 4.
| Дидактичний матеріал для організації повторення
|
|
| 5.
| Діагностичні контрольні роботи
|
|
| |
|
|
КАЛЕНДАРНО– ТЕМАТИЧНЕ ПЛАНУВАННЯ
ГЕОМЕТРІЯ, 11 КЛАС
(2 години на тиждень, всього за рік - 70 годин)
| №
| Тема уроку
| Примітка
|
| Тема 1. Узагальнення та систематизація навчального матеріалу. (4 годин)
|
|
|
| Система опорних фактів з планіметрії. Координати та вектори на площині.
|
|
|
| Аксіоми стереометрії, їх наслідки. Паралельність і перпендикулярність прямих і площин.
|
|
|
| Вимірювання кутів та відстаней у просторі.
|
|
|
| Діагностична контрольна робота (№1)
|
|
| Тема 2. Координати, геометричні перетворення та вектори у просторі. (16 годин)
|
|
|
| Прямокутна система координат у просторі. Відстань між точками. Координати середини відрізка.
|
|
|
| Відстань між точками. Координати середини відрізка.
|
|
|
| Перетворення у просторі та їх властивості.
|
|
|
| Перетворення у просторі та їх властивості.
|
|
|
| Вектори у просторі. Рівність, колінеарність та компланарність векторів.
|
|
|
| Додавання та віднімання векторів, множення вектора на число.
|
|
|
| Додавання та віднімання векторів, множення вектора на число. Самостійна робота.
|
|
|
| Кут між векторами. Скалярний добуток векторів.
|
|
|
| Кут між векторами. Скалярний добуток векторів.
|
|
|
| Розв’язування задач. Розкладання вектора за трьома не компланарними векторами.
|
|
|
| Рівняння площини.
|
|
|
| Рівняння сфери.
|
|
|
| Розв’язування задач.
|
|
|
| Розв’язування задач. Самостійна робота.
|
|
|
| Розв’язування задач.
|
|
|
| Тематична контрольна робота (№2)
|
|
| Тема 3. Многогранники. (16 годин)
|
|
|
| Двогранні, многогранні кути. Лінійний кут двогранного кута.
|
|
|
| Многогранники. Опуклі многогранники. Призма.
|
|
|
| Зображення призми та побудова перерізів.
|
|
|
| Пряма і правильна призма. Бічна і повна поверхні призми.
|
|
|
| Розв’язування задач. Самостійна робота.
|
|
|
| Паралелепіпед та його властивості. Прямокутний паралелепіпед.
|
|
|
| Піраміда.
|
|
|
| Побудова піраміди та її перерізів.
|
|
|
| Правильна піраміда. Бічна поверхня правильної піраміди.
|
|
|
| Розв’язування задач. Самостійна робота.
|
|
|
| Правильні многогранники.
|
|
|
| Розв’язування задач.
|
|
|
| Розв’язування задач.
|
|
|
| Розв’язування задач. Самостійна робота.
|
|
|
| Розв’язування задач.
|
|
|
| Тематична контрольна робота (№3)
|
|
| Тема 4. Тіла обертання. (14 годин)
|
|
|
| Тіла і поверхні обертання. Циліндр, його елементи. Переріз циліндра площиною.
|
|
|
| Вписана й описана призми.
|
|
|
| Конус. Зрізаний конус, його елементи. Переріз конуса площиною.
|
|
|
| Вписана й описана піраміди.
|
|
|
| Розв’язування задач. Самостійна робота.
|
|
|
| Куля і сфера. Переріз кулі площиною. Симетрія кулі.
|
|
|
| Площина, дотична до сфери. Вписані й описані многогранники.
|
|
|
| Розв’язування задач.
|
|
|
| Вписані многогранники і тіла обертання.
|
|
|
| Описані многогранники і тіла обертання.
|
|
|
| Розв’язування вправ на комбінації просторових фігур.
|
|
|
| Розв’язування вправ. Самостійна робота.
|
|
|
| Розв’язування вправ.
|
|
|
| Тематична контрольна робота (№4)
|
|
| Тема 5. Об’єми та площі поверхонь геометричних тіл.
(14 годин)
|
|
|
| Поняття про об’єм тіла. Основні властивості об’ємів. Об’єм паралелепіпеда.
|
|
|
| Об’єм призми.
|
|
|
| Об’єм піраміди.
|
|
|
| Розв’язування вправ. Самостійна робота.
|
|
|
| Об’єм циліндра.
|
|
|
| Об’єм конуса.
|
|
|
| Об’єм кулі та її частин.
|
|
|
| Розв’язування вправ. Самостійна робота.
|
|
|
| Площі бічної і повної поверхонь циліндра.
|
|
|
| Площі бічної і повної поверхонь конуса.
|
|
|
| Площа сфери.
|
|
|
| Розв’язування вправ. Самостійна робота.
|
|
|
| Розв’язування вправ.
|
|
|
| Тематична контрольна робота (№5)
|
|
| Тема 6. Повторення, узагальнення та систематизація навчального матеріалу, розв’язування задач. (6 годин)
|
|
|
| Паралельність і перпендикулярність прямих і площин. Вимірювання кутів та відстаней у просторі.
|
|
|
| Многогранники. Тіла обертання.
|
|
|
| Об’єми та площі поверхонь геометричних тіл.
|
|
|
| Контрольна робота(№6)
|
|
|
| Розв’язування вправ.
|
|
|
| Розв’язування вправ.
|
|
ДОВІДКОВИЙ МАТЕРІАЛ З ТЕМИ
| Взаємне розміщення прямих і площин у просторі
|
| кількість спільних точок
|
| не менше двох
| одна
| Відсутні
|
|
|
|
|
| а Ì a
а лежить в a
| а ´ a
а перетинає a
| а | | a
а і a паралельні
|
| Взаємне розміщення площин у просторі
|
| кількість спільних точок
|
| не менше трьох, що не
лежать на одній прямій
| не менше однієї, але
немає спільних точок, які
не лежать на одній прямій
| Відсутні
|
|
|
|
|
| a і b збігаються
a = b
| a і b перетинаються
a ´ b
| a і b паралельні
a | | b
|
| Для того, щоб зафіксувати площину в просторі можна задати:
|
| Ø три точки, що не лежать на одній прямій
|
|
| Ø пряму і точку, що не лежать на цій прямій
|
|
| Ø дві різні прямі, що перетинаються
|
|
| Ø дві паралельні прямі
|
|
| Для встановлення паралельності двох прямих в просторі можна перевірити:
|
| Ø чи знайдеться пряма, паралельна кожній із даних прямих
|
|
| Ø чи будуть дані прямі лініями перетину двох паралельних площин третьою.
|
|
| Ø чи буде одна із даних прямих лінією перетину двох площин, одна з яких паралельна даній прямій, а інша проходить через цю пряму.
|
|
| Для встановлення мимобіжності двох прямих в просторі необхідно перевірити:
|
| Ø Чи знайдеться площина, у якій лежить одна з даних прямих і яку перетинає друга пряма у точці, що не належить першій прямій.
|
|
| Для встановлення паралельності прямої і площини необхідно перевірити:
|
| Ø чи знайдеться в площині пряма паралельна даній прямій
|
|
| Для встановлення паралельності двох площин можна перевірити:
|
| Ø чи знайдуться в одній із площин дві прямі, що перетинаються і відповідно паралельні двом прямим другої площини
|
|
| Ø чи знайдеться площина, паралельна кожній з даних площин
|
|
Основні формули та теореми
| Паралельні прямі
Ознаки
|
| 1. Дві прямі паралельні, якщо з січною вони утворюють рівні відповідні кути.
2. Дві прямі паралельні, якщо з січною вони утворюють рівні внутрішні різносторонні кути.
3. Дві прямі паралельні, якщо сума односторонніх кутів, що утворюються з січною, дорівнює 180°.
4. Дві прямі, перпендикулярні до третьої, паралельні між собою.
5. Дві прямі, паралельні третій, паралельні між собою.
|
| Властивості
|
| 1. Відповідні кути, що утворені паралельними прямими з їх січною, рівні.
2. Внутрішні різносторонні кути, утворені паралельними прямими з їх січною, рівні.
3. Сума односторонніх кутів (внутрішніх або зовнішніх), утворених паралельними прямими з січною, дорівнює 180°.
|
| Теорема Фалеса
|
| Якщо паралельні прямі, що перетинають сторони кута, відтинають на одній його стороні рівні між собою відрізки, то вони відтинають рівні між собою відрізки і на другій його стороні.
|
Трикутник
| Рисунок
| Позначення
| Формули
|
  
| a, b, c – сторони
А, В, С – кути
hb – висота, проведена з вершини В
R – радіус описаного кола
r – радіус вписаного кола
S – площа трикутника
р – півпериметр
ma – медіана до сторони а
|  (формула Герона)
(формула Герона)
 (теорема косинусів)
(теорема косинусів)
 (теорема синусів)
(теорема синусів)
|
| Основні теореми
Теорема про суму кутів трикутників
Сума внутрішніх кутів трикутника дорівнює 180°.
Теорема про середню лінію трикутника
Відрізок, який з’єднує середини двох сторін трикутника, паралельний до третьої сторони та дорівнює його половині.
Ознаки рівності трикутників
1. Якщо дві сторони та кут між ними одного трикутника дорівнюють відповідно двом сторонам і куту між ними другого трикутника, то такі трикутники рівні.
2. Якщо сторона та два прилеглі до неї кута одного трикутника дорівнюють відповідно стороні та двом прилеглим до неї кутам другого трикутника, то такі трикутники рівні.
3. Якщо три сторони одного трикутника рівні відповідно трьом сторонам другого трикутника, то такі трикутники рівні.
Ознаки подібності трикутників
1.Якщо два кута одного трикутника відповідно рівні двом кутам другого трикутника, то такі трикутники подібні.
2. Якщо дві сторони одного трикутника пропорційні двом сторонам другого і кути, утворені цими сторонами, рівні, то такі трикутники подібні.
3. Якщо три сторони одного трикутника пропорційні трьом сторонам другого, то такі трикутники подібні.
Вписані та описані трикутники
1. Навколо будь-якого трикутника можна описати коло і тільки одне. Центр описаного кола співпадає з точкою перетину серединних перпендикулярів до сторін трикутника.
2. В будь-який трикутник можна вписати коло і тільки одне. Центр вписаного кола лежить на перетині бісектрис кутів трикутника.
Властивості медіан, бісектрис та висот трикутника
1. Медіани трикутника перетинаються в одній точці та поділяються точкою перетину у відношенні 2:1, рахуючи від вершини.
2. Бісектриси кутів трикутника перетинаються в одній точці.
3. Бісектриса внутрішнього кута трикутника поділяє протилежну сторону на частини, пропорційні прилеглим сторонам.
4. Висоти трикутника (або їх продовження) перетинаються в одній точці.
|
Прямокутний трикутник
| Рисунок
| Позначення
| Формули
|

| A, b – катети
с – гіпотенуза
b¢, a¢ - проекції катетів на гіпотенузу
mc – медіана, проведена до гіпотенузи
R – радіус описаного кола
О – центр описаного кола
|  (теорема Піфагора)
(теорема Піфагора)

|
Основні теореми
Теорема Піфагора
У прямокутному трикутнику квадрат гіпотенузи дорівнює сумі квадратів катетів.
Метричні співвідношення
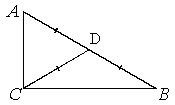
1. Висота CD, яка проведена до гіпотенузи AB прямокутного трикутника ABC, поділяє цей трикутник на два трикутники, подібні між собою та подібні даному трикутнику.
Звідси: CD 2 = AD·BD; BC 2 = AB · AD; BC 2 = AB · BD.
 2. Медіана, яка проведена з вершини прямого кута прямокутного трикутника, дорівнює половині гіпотенузи. 2. Медіана, яка проведена з вершини прямого кута прямокутного трикутника, дорівнює половині гіпотенузи.
3. Центр кола, описаного навколо прямокутного трикутника, співпадає з серединою гіпотенузи, а його радіус дорівнює половині гіпотенузи.
R = AO = BO = CO =  AB. AB.
 4. Сума довжин катетів прямокутного трикутника дорівнює сумі довжин діаметрів вписаного та описаного кіл. 4. Сума довжин катетів прямокутного трикутника дорівнює сумі довжин діаметрів вписаного та описаного кіл.
а + b = 2R+2r
|
Правильний трикутник
| Рисунок
| Позначення
| Формули
|

| а – сторона
h – висота
R – радіус описаного кола
r – радіус вписаного кола
S – площа
| 
|
Рівнобедрений трикутник
Основні теореми
Властивості
Ознаки
1. Якщо у трикутнику два кута рівні, то він рівнобедрений.
2. Якщо висота трикутника одночасно є і медіаною, то трикутник рівнобедрений.
3. Якщо медіана трикутника одночасно є і бісектрисою, то трикутник рівнобедрений.
4. Якщо бісектриса кута трикутника одночасно є і висотою, то трикутник рівнобедрений.
Чотирикутник
| Рисунок
| Основні теореми
|
Навколо опуклого чотирикутника можна описати коло тоді і тільки тоді, коли сума протилежних кутів становить 180°: 

В опуклий чотирикутник можна вписати коло тоді і тільки тоді, коли суми протилежних сторін рівні:

|
Паралелограм
| Рисунок
| Позначення
| Формули
|

| a, b – сторони
hb – висота до сторони b
d 1, d 2 – діагоналі
S – площа
a - кут паралелограма
j - кут між діагоналями
| 
|
| Основні теореми
Властивості
1. Протилежні сторони паралелограма рівні, та протилежні кути паралелограма рівні.
2. Діагоналі паралелограма поділяються точкою перетину навпіл.
Ознаки
1. Якщо в чотирикутнику дві протилежні сторони рівні та паралельні, то такий чотирикутник – паралелограм.
2. Якщо в чотирикутнику протилежні сторони попарно рівні, то такий чотирикутник – паралелограм.
3. Якщо у чотирикутника діагоналі діляться точкою перетину навпіл, то такий чотирикутник – паралелограм.
|
Прямокутник та ромб
Властивості
1. Діагоналі прямокутник рівні.
2. Діагоналі ромба взаємно перпендикулярні та ділять кути ромба навпіл.
Ознаки
1. Якщо у паралелограма діагоналі рівні, то такий паралелограм – прямокутник.
2. Якщо у паралелограма діагоналі перпендикулярні, то такий паралелограм – ромб.
3. Якщо у паралелограма діагоналі ділять його кути навпіл, то такий паралелограм – ромб.
| Трапеція
|
| Рисунок
| Позначення
| Формули
|

| a, b – основи
h – висота
t – середня лінія
S – площа
| 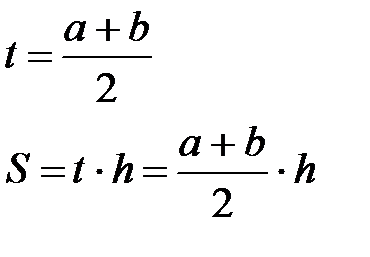
|
| Основні властивості
Середня лінія трапеції паралельна основам та дорівнює їх півсумі.
|
| Круг і коло
|
| Рисунок
| Позначення
| Формули
|


|
R – радіус кола
с – довжина кола
S – площа круга
l – довжина дуги кола
Sc – площа сектора
a - радіанна міра центрального кута, який відповідає дузі
п – градусна міра центрального кута, який відповідає дузі
| Центральний кут вимірюється дугою, на яку він спирається.
 .
Вписаний кут вимірюється половиною дуги, на яку він спирається. .
Вписаний кут вимірюється половиною дуги, на яку він спирається.
 .
Кут між дотичною і хордою, що проведені через деяку точку кола, вимірюється половиною дуги, що знаходиться між ними. .
Кут між дотичною і хордою, що проведені через деяку точку кола, вимірюється половиною дуги, що знаходиться між ними.
 c = 2pR S =pR 2
c = 2pR S =pR 2


|
|
|
|
|
| Метричні співвідношення у колі
Якщо хорди AB і CD перетинаються в точці M у внутрішній частині кола, то 

Якщо із точки М, що лежить поза колом, провести до кола січну MAB і дотичну MC, то  . .
|
| | | | | |
Вектор
Вектор - це величина, яка характеризується числовим значенням і напрямком. Під направленим відрізком  розуміють впорядковану пару точок, перша з яких - точка A - називається його початком, а друга - B - його кінцем.
розуміють впорядковану пару точок, перша з яких - точка A - називається його початком, а друга - B - його кінцем.
Вектори позначають двома способами:
· малими буквами латинського алфавіту (наприклад,  );
);
·  двома великими буквами латинського алфавіту (наприклад,
двома великими буквами латинського алфавіту (наприклад,  ), де перша буква - початок вектора, а друга - кінець.
), де перша буква - початок вектора, а друга - кінець.
Графічно вектори зображають у вигляді направлених відрізків певної довжини  .
.
Рис.1. Вектор AB
з початком в A і кінцем в B.
Примітка. Поняття вектора з'явилося в роботах німецького математика XIX ст. Г. Грассмана та ірландського математика У. Гамільтона.
Чисельне значення вектора  називається модулем чи довжиною і позначається |
називається модулем чи довжиною і позначається |  |. Довжина вектора - це довжина відрізка, що зображає цей вектор.
|. Довжина вектора - це довжина відрізка, що зображає цей вектор.
Вектори  і
і  називають протилежно напрямленими, якщо протилежно напрямлені півпрямі
називають протилежно напрямленими, якщо протилежно напрямлені півпрямі  і
і 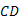 .
.
Вектори  і
і  називають співнапрямленими, якщо співнапрямлені півпрямі
називають співнапрямленими, якщо співнапрямлені півпрямі  і
і 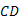 .
.
 Рис.2. Протилежно напрямлені вектори. Рис.3. Співнапрямлені вектори.
Рис.2. Протилежно напрямлені вектори. Рис.3. Співнапрямлені вектори.

Вектор, початок і кінець якого збігаються, називається нульовим і позначається  . Нульовий вектор має довжину 0. Напрям нульового вектора не визначений. Нульовий вектор прийнято рахувати співнапрямленим з будь-яким вектором. Вважається, що нульовий вектор одночасно паралельний і перпендикулярний будь-якому вектору.
. Нульовий вектор має довжину 0. Напрям нульового вектора не визначений. Нульовий вектор прийнято рахувати співнапрямленим з будь-яким вектором. Вважається, що нульовий вектор одночасно паралельний і перпендикулярний будь-якому вектору.
Колінеарними називаються вектори, які зображаються відрізками, що лежать на одній прямій чи на паралельних прямих.
Два вектора називаються рівними, якщо вони однієї довжини і їх напрямки збігаються.
Одиничний вектор (орт) - вектор, довжина якого рівна одиниці.
Числа  ,
,  називаються координатами вектора
називаються координатами вектора  з початком
з початком  і кінцем
і кінцем  .
.
Примітка. Всі координати нульового вектора дорівнюють нулю.
Примітка. Вектори рівні, коли їх відповідні координати рівні.
Вектор з координатами  і
і 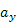 позначається
позначається  .
.
Вектор  з координатами
з координатами  і
і 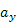 позначається
позначається  .
.
Використовуючи означення координат вектора довжину можна записати формулою  .
.
Правило трикутника
 Для складання двох векторів
Для складання двох векторів  і
і  за правилом трикутника обидва ці вектора переносяться паралельно самим собі так, щоб початок одного з них збігався з кінцем іншого. Тоді вектор суми задається третьою стороною трикутника, що утворився, причому його початок збігається з початком першого вектора.
за правилом трикутника обидва ці вектора переносяться паралельно самим собі так, щоб початок одного з них збігався з кінцем іншого. Тоді вектор суми задається третьою стороною трикутника, що утворився, причому його початок збігається з початком першого вектора.
Правило паралелограма

 Для складання двох векторів
Для складання двох векторів  і
і  за правилом паралелограма обидва ці вектора переносяться паралельно самим собі так, щоб їх початки збігалися. Тоді вектор суми задається діагоналлю побудованого на них паралелограма, яка виходить з їх спільного початку.
за правилом паралелограма обидва ці вектора переносяться паралельно самим собі так, щоб їх початки збігалися. Тоді вектор суми задається діагоналлю побудованого на них паралелограма, яка виходить з їх спільного початку.
Різницею векторів  і
і  називають такий вектор
називають такий вектор  , який в сумі з
, який в сумі з  дає
дає  .
.
Добуток вектора  на число
на число  називається вектор
називається вектор  .
.
Два вектори  і
і  колінеарні тоді і лише тоді, коли їх відповідні координати пропорційні
колінеарні тоді і лише тоді, коли їх відповідні координати пропорційні  .
.
Скалярним добутком векторів  і
і  називається число, яке рівне сумі добутків відповідних координат, тобто
називається число, яке рівне сумі добутків відповідних координат, тобто  .
.
Скалярний добуток векторів дорівнює добутку їх довжин на косинус кута між ними, тобто  , де
, де  - кут між векторами
- кут між векторами  і
і  .
.
Варіанти завдань
| 1.А(-3; 5) В(- 3; 8) С(2;10) D(2; 7)
| 14.А(2;3) В(3;5) С(10;1) D(11;-2)
| 27.А(-2;-2) В(-4;-6) С(4;-10) D(6;-6)
|
| 2.А(- 9; 1) В(- 7; 5) С(-3;7) D(-5; 3)
| 15.А(7;-1) В(4;-4)
С(-2;-6) D(1;-3)
| 28.А(-8;-2) В(-10;1)
С(-4;5) D(1;4)
|
| 3.А(0; 0) В(0; 2)
С(6;8) D(10; 10)
| 16.А(-7;-2) В(-1;-3) С(0;-10) D(-7;-9)
| 29.А(-6;-1) В(0;1) С(6;1) D(0;-1)
|
| 4.А(-2;1) В(-1;6) С(-6;7) D(-7;2)
| 17.А(-9;4) В(-8;7)
С(-5;9) D(0;10)
| 30.А(0;0) В(4;-1) С(5;-5) D(1;-4)
|
| 5.А(-2;-2) В(0;2) С(6;8) D(10;10)
| 18.А(4;-1) В(7;-4) С(4;-7) D(1;-4)
| 31.А(-7;4) В(-3;2)
С(-1;-2) D(-3;-4)
|
| 6.А(2;3) В(3;5) С(10;1) D(9;-1)
| 19.А(9;-4) В(11;2) С(12;2) D(14;-4)
| 32.А(-2;0) В(-1;4) С(3;3) D(2;-1)
|
| 7.А(-3;1) В(-1;7) С(2;6) D(-1;-3)
| 20.А(-8;-2) В(-10;1) С(-1;7) D(1;4)
| 33.А(-3;-2) В(-4;4) С(4;-4) D(-2;-3)
|
| 8.А(-14;-2) В(-11;2) С(-3;2) D(-6;-2)
| 21.А(-4;-6) В(-2;-2) С(2;-4) D(4;-10)
| 34.А(-2;-1) В(-2;-2) С(7;-2) D(7;-1)
|
| 9.А(6;0) В(5;-5) С(0;-6) D(1;-1)
| 22.А(0;6) В(5;4) С(7;0) D(2;2)
| 35.А(-2;-1) В(-2;-2) С(7;-2) D(3;-1)
|
| 10.А(-4;-10) В(0;-6) С(4;-6) D(2;-10)
| 23.А(0;2) В(1;5) С(0;8) D(-1;5)
| 36.А(0;-6) В(4;-4)
С(4;-8) D(0;-10)
|
| 11.А(-5;-1) В(-2;-3)
С(-4;-6) D(-7;-4)
| 24.А(0;2) В(0;6) С(3;9) D(6;8)
| 37.А(7;0) В(10;2) С(13;0) D(10;-2)
|
| 12.А(-4;-10) В(0;-6) С(4;-6) D(8;-10)
| 25.А(3;0) В(1;3) С(7;2) D(6;-1)
| 38.А(4;-4) В(5;0) С(8;0) D(13;-4)
|
| 13.А(-3;1) В(-1;7)
С(2;6) D(0;0)
| 26.А(0;2) В(0;6) С(3;9) D(7;9)
| |
Математичний диктант №1
Варіант 1
1.Запишіть коротко «вектор а».
2. Зобразити вектор  .
3.Запишіть позначення вектора з кінцем у точці Х та початком у точці У.
4.Зобразити два однаково спрямованих, але не рівних вектора.
5.Що можна сказати про напрямок двох рівних векторів?
6.Запишіть у вигляді рівності, чому дорівнює абсолютна величина нульового вектора.
7. Зобразити вектор .
3.Запишіть позначення вектора з кінцем у точці Х та початком у точці У.
4.Зобразити два однаково спрямованих, але не рівних вектора.
5.Що можна сказати про напрямок двох рівних векторів?
6.Запишіть у вигляді рівності, чому дорівнює абсолютна величина нульового вектора.
7. Зобразити вектор  і точку У. Відкладіть від точки У вектор, рівний і точку У. Відкладіть від точки У вектор, рівний  .
8. Запишіть за допомогою позначень «довжина вектора .
8. Запишіть за допомогою позначень «довжина вектора  дорівнює 3 см».
9.Знайдіть довжину вектора, зображеного на рисунку:
Т
3 см
S 5 см
10. Чи вірно твердження: «Якщо вектори дорівнює 3 см».
9.Знайдіть довжину вектора, зображеного на рисунку:
Т
3 см
S 5 см
10. Чи вірно твердження: «Якщо вектори  й й  рівні, то вони колінеарні»? рівні, то вони колінеарні»?
| Математичний диктант №1
Варіант 2
1.Запишіть коротко «вектор в».
2. Зобразити вектор 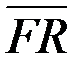 .
3.Запишіть позначення вектора з кінцем у точці Р та початком у точці А.
4.Запишіть у вигляді рівності, чому дорівнює абсолютна величина нульового вектора.
5. Зобразити вектор .
3.Запишіть позначення вектора з кінцем у точці Р та початком у точці А.
4.Запишіть у вигляді рівності, чому дорівнює абсолютна величина нульового вектора.
5. Зобразити вектор  і точку М. Відкладіть від точки М вектор, який дорівнює вектору і точку М. Відкладіть від точки М вектор, який дорівнює вектору  .
6.Що можна сказати про напрямок двох рівних векторів?
7.Зобразити два однаково спрямованих, але не рівних вектора.
8. Запишіть за допомогою позначень «довжина вектора .
6.Що можна сказати про напрямок двох рівних векторів?
7.Зобразити два однаково спрямованих, але не рівних вектора.
8. Запишіть за допомогою позначень «довжина вектора 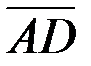 дорівнює 4 см».
9.Знайдіть довжину вектора, зображеного на малюнку:
М
К 2 см
6 см
10. Чи вірно твердження: «Якщо два вектори колінеарні, то вони однаково спрямовані»? дорівнює 4 см».
9.Знайдіть довжину вектора, зображеного на малюнку:
М
К 2 см
6 см
10. Чи вірно твердження: «Якщо два вектори колінеарні, то вони однаково спрямовані»?
|
Математичний диктант №2
Варіант 1
1. Знайдіть координати вектора  , де А(1;3), В(-2;0).
2. Знайдіть довжину вектора , де А(1;3), В(-2;0).
2. Знайдіть довжину вектора
 (-3;4).
3. Знайдіть суму векторів (-3;4).
3. Знайдіть суму векторів  (-3;2) і (-3;2) і  (-4;5).
4. Чи колінеарні вектори (-4;5).
4. Чи колінеарні вектори  (-1;2) і (-1;2) і  (2;-4)?
5. Знайдіть скалярний добуток векторів (2;-4)?
5. Знайдіть скалярний добуток векторів  (1;5) і (1;5) і  (-3;-2).
6. Знайдіть скалярний добуток векторів (-3;-2).
6. Знайдіть скалярний добуток векторів  й й  , якщо , якщо 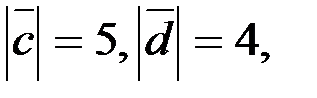 а кут між цими векторами дорівнює 300.
7. Чи перпендикулярні вектори а кут між цими векторами дорівнює 300.
7. Чи перпендикулярні вектори
 (-2;3) і (-2;3) і  (-1;2)?
8. Знайдіть кут між векторами (-1;2)?
8. Знайдіть кут між векторами  (1;1) і (1;1) і  (1;0).
9. Знайдіть косинус кута між векторами (1;0).
9. Знайдіть косинус кута між векторами  (-3;1) і (-3;1) і  (3;-4).
10. Вектор (3;-4).
10. Вектор  має координати (-3;8), а точка F(5;2). Знайдіть координати точки К. має координати (-3;8), а точка F(5;2). Знайдіть координати точки К.
| Математичний диктант №2
Варіант 2
1. Знайдіть координати вектора  , де А(2;4), В(-3;0).
2. Знайдіть довжину вектора , де А(2;4), В(-3;0).
2. Знайдіть довжину вектора
 (6;-8).
3. Знайдіть суму векторів (6;-8).
3. Знайдіть суму векторів  (-2;3) і (-2;3) і  (-4;7).
4. Чи колінеарні вектори (-4;7).
4. Чи колінеарні вектори  (-2;4) і (-2;4) і  (6;-5)?
5. Знайдіть скалярний добуток векторів (6;-5)?
5. Знайдіть скалярний добуток векторів  (3;4) і (3;4) і  (-2;1).
6. Знайдіть скалярний добуток векторів (-2;1).
6. Знайдіть скалярний добуток векторів  й й  , якщо , якщо  а кут між цими векторами дорівнює 450.
7. Чи перпендикулярні вектори а кут між цими векторами дорівнює 450.
7. Чи перпендикулярні вектори  (-3;2) і (-3;2) і  (4;6)?
8. Знайдіть кут між векторами (4;6)?
8. Знайдіть кут між векторами  (2;2) і (2;2) і  (0;2).
9. Знайдіть косинус кута між векторами (0;2).
9. Знайдіть косинус кута між векторами  (-2;1) і (-2;1) і  (4;-3).
10. Вектор (4;-3).
10. Вектор  має координати (-4;-3), а точка F(1;3). Знайдіть координати точки К. має координати (-4;-3), а точка F(1;3). Знайдіть координати точки К.
|
Варіант 3
1. Знайдіть координати вектора  , де А(3;5), В(-3;2).
2. Знайдіть довжину вектора , де А(3;5), В(-3;2).
2. Знайдіть довжину вектора
 (2;-4).
3. Знайдіть суму векторів (2;-4).
3. Знайдіть суму векторів  (-4;2) і (-4;2) і  (5;7).
4. Чи колінеарні вектори (5;7).
4. Чи колінеарні вектори  (8;-4) і (8;-4) і  (-2;-1)?
5.Знайдіть скалярний добуток векторів (-2;-1)?
5.Знайдіть скалярний добуток векторів  (4;2) і (4;2) і  (-2;1).
6. Знайдіть скалярний добуток векторів (-2;1).
6. Знайдіть скалярний добуток векторів  й й  , якщо , якщо  а кут між цими векторами дорівнює 1500.
7. Чи перпендикулярні вектори а кут між цими векторами дорівнює 1500.
7. Чи перпендикулярні вектори 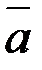 (3;2) і (3;2) і  (-4;6)?
8. Знайдіть кут між векторами (-4;6)?
8. Знайдіть кут між векторами
 (-1;1) і (-1;1) і  (-1;0).
9.Знайдіть косинус кута між векторами (-1;0).
9.Знайдіть косинус кута між векторами  (3;1) і (3;1) і  (3;4).
10. Вектор (3;4).
10. Вектор  має координати (2;11), а точка F(2;-3). Знайдіть координати точки К. має координати (2;11), а точка F(2;-3). Знайдіть координати точки К.
| Варіант 4
1. Знайдіть координати вектора  , де А(4;6), В(-2;4).
2. Знайдіть довжину вектора , де А(4;6), В(-2;4).
2. Знайдіть довжину вектора
 (-8;2).
3. Знайдіть суму векторів (-8;2).
3. Знайдіть суму векторів  (2;-6) і (2;-6) і  (4;-8).
4. Чи колінеарні вектори (4;-8).
4. Чи колінеарні вектори  (7;-3) і (7;-3) і  (1;-4)?
5.Знайдіть скалярний добуток векторів (1;-4)?
5.Знайдіть скалярний добуток векторів  (3;2) і (3;2) і  (-4;6).
6. Знайдіть скалярний добуток векторів (-4;6).
6. Знайдіть скалярний добуток векторів  й й  , якщо , якщо  а кут між цими векторами дорівнює 1350.
7. Чи перпендикулярні вектори а кут між цими векторами дорівнює 1350.
7. Чи перпендикулярні вектори  (4;2) і (4;2) і  (-2;1)?
8. Знайдіть кут між векторами (-2;1)?
8. Знайдіть кут між векторами
 (-2;2) і (-2;2) і  (0;-2).
9.Знайдіть косинус кута між векторами (0;-2).
9.Знайдіть косинус кута між векторами  (2;1) і (2;1) і  (4;3).
10. Вектор (4;3).
10. Вектор  має координати (-9;10), а точки F(4;-3). Знайдіть координати точки К. має координати (-9;10), а точки F(4;-3). Знайдіть координати точки К.
|
Питання для обговорення до теми: «Основні поняття й аксіоми стереометрії»
1. Чи можуть три точки розташовуватися так, щоб через них можна було провести дві різні площини?
2. Чи можуть лежати в одній площині тільки три вершини паралелограма?
3. Чи можуть дві площини мати тільки одну спільну точку?
4. Чи вірно, що трикутник лежить у площині, якщо його вершини лежать у цій площині?
5. Чи завжди пряма, що перетинає кожну із двох прямих, які перетинаються, лежить із ними в одній площині?


 і
і  збігаються
збігаються 
 і
і  перети-наються (а ´
перети-наються (а ´  )
)
 і
і  паралельні
(а êú
паралельні
(а êú 
 )
)



 (формула Герона)
(формула Герона)
 (теорема косинусів)
(теорема косинусів)
 (теорема синусів)
(теорема синусів)

 (теорема Піфагора)
(теорема Піфагора)

 2. Медіана, яка проведена з вершини прямого кута прямокутного трикутника, дорівнює половині гіпотенузи.
2. Медіана, яка проведена з вершини прямого кута прямокутного трикутника, дорівнює половині гіпотенузи.
 AB.
AB. 4. Сума довжин катетів прямокутного трикутника дорівнює сумі довжин діаметрів вписаного та описаного кіл.
4. Сума довжин катетів прямокутного трикутника дорівнює сумі довжин діаметрів вписаного та описаного кіл.







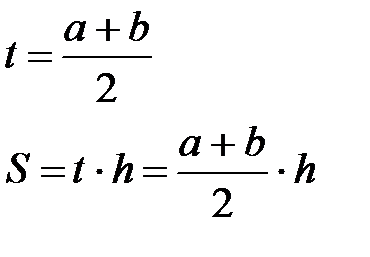


 .
Вписаний кут вимірюється половиною дуги, на яку він спирається.
.
Вписаний кут вимірюється половиною дуги, на яку він спирається.
 .
Кут між дотичною і хордою, що проведені через деяку точку кола, вимірюється половиною дуги, що знаходиться між ними.
.
Кут між дотичною і хордою, що проведені через деяку точку кола, вимірюється половиною дуги, що знаходиться між ними.
 c = 2pR S =pR 2
c = 2pR S =pR 2




 .
. розуміють впорядковану пару точок, перша з яких - точка A - називається його початком, а друга - B - його кінцем.
розуміють впорядковану пару точок, перша з яких - точка A - називається його початком, а друга - B - його кінцем. );
); двома великими буквами латинського алфавіту (наприклад,
двома великими буквами латинського алфавіту (наприклад,  називається модулем чи довжиною і позначається |
називається модулем чи довжиною і позначається |  називають протилежно напрямленими, якщо протилежно напрямлені півпрямі
називають протилежно напрямленими, якщо протилежно напрямлені півпрямі  і
і 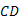 .
. Рис.2. Протилежно напрямлені вектори. Рис.3. Співнапрямлені вектори.
Рис.2. Протилежно напрямлені вектори. Рис.3. Співнапрямлені вектори.
 . Нульовий вектор має довжину 0. Напрям нульового вектора не визначений. Нульовий вектор прийнято рахувати співнапрямленим з будь-яким вектором. Вважається, що нульовий вектор одночасно паралельний і перпендикулярний будь-якому вектору.
. Нульовий вектор має довжину 0. Напрям нульового вектора не визначений. Нульовий вектор прийнято рахувати співнапрямленим з будь-яким вектором. Вважається, що нульовий вектор одночасно паралельний і перпендикулярний будь-якому вектору. ,
,  називаються координатами вектора
називаються координатами вектора  і кінцем
і кінцем  .
. і
і 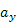 позначається
позначається  .
. .
. .
. Для складання двох векторів
Для складання двох векторів  за правилом трикутника обидва ці вектора переносяться паралельно самим собі так, щоб початок одного з них збігався з кінцем іншого. Тоді вектор суми задається третьою стороною трикутника, що утворився, причому його початок збігається з початком першого вектора.
за правилом трикутника обидва ці вектора переносяться паралельно самим собі так, щоб початок одного з них збігався з кінцем іншого. Тоді вектор суми задається третьою стороною трикутника, що утворився, причому його початок збігається з початком першого вектора.
 Для складання двох векторів
Для складання двох векторів  , який в сумі з
, який в сумі з  називається вектор
називається вектор  .
. .
. .
. , де
, де  - кут між векторами
- кут між векторами  .
3.Запишіть позначення вектора з кінцем у точці Х та початком у точці У.
4.Зобразити два однаково спрямованих, але не рівних вектора.
5.Що можна сказати про напрямок двох рівних векторів?
6.Запишіть у вигляді рівності, чому дорівнює абсолютна величина нульового вектора.
7. Зобразити вектор
.
3.Запишіть позначення вектора з кінцем у точці Х та початком у точці У.
4.Зобразити два однаково спрямованих, але не рівних вектора.
5.Що можна сказати про напрямок двох рівних векторів?
6.Запишіть у вигляді рівності, чому дорівнює абсолютна величина нульового вектора.
7. Зобразити вектор  і точку У. Відкладіть від точки У вектор, рівний
і точку У. Відкладіть від точки У вектор, рівний  .
8. Запишіть за допомогою позначень «довжина вектора
.
8. Запишіть за допомогою позначень «довжина вектора  дорівнює 3 см».
9.Знайдіть довжину вектора, зображеного на рисунку:
Т
3 см
S 5 см
10. Чи вірно твердження: «Якщо вектори
дорівнює 3 см».
9.Знайдіть довжину вектора, зображеного на рисунку:
Т
3 см
S 5 см
10. Чи вірно твердження: «Якщо вектори  й
й  рівні, то вони колінеарні»?
рівні, то вони колінеарні»?
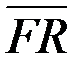 .
3.Запишіть позначення вектора з кінцем у точці Р та початком у точці А.
4.Запишіть у вигляді рівності, чому дорівнює абсолютна величина нульового вектора.
5. Зобразити вектор
.
3.Запишіть позначення вектора з кінцем у точці Р та початком у точці А.
4.Запишіть у вигляді рівності, чому дорівнює абсолютна величина нульового вектора.
5. Зобразити вектор  і точку М. Відкладіть від точки М вектор, який дорівнює вектору
і точку М. Відкладіть від точки М вектор, який дорівнює вектору  .
6.Що можна сказати про напрямок двох рівних векторів?
7.Зобразити два однаково спрямованих, але не рівних вектора.
8. Запишіть за допомогою позначень «довжина вектора
.
6.Що можна сказати про напрямок двох рівних векторів?
7.Зобразити два однаково спрямованих, але не рівних вектора.
8. Запишіть за допомогою позначень «довжина вектора 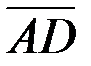 дорівнює 4 см».
9.Знайдіть довжину вектора, зображеного на малюнку:
М
К 2 см
6 см
10. Чи вірно твердження: «Якщо два вектори колінеарні, то вони однаково спрямовані»?
дорівнює 4 см».
9.Знайдіть довжину вектора, зображеного на малюнку:
М
К 2 см
6 см
10. Чи вірно твердження: «Якщо два вектори колінеарні, то вони однаково спрямовані»?
 , де А(1;3), В(-2;0).
2. Знайдіть довжину вектора
, де А(1;3), В(-2;0).
2. Знайдіть довжину вектора
 (-3;4).
3. Знайдіть суму векторів
(-3;4).
3. Знайдіть суму векторів  (-3;2) і
(-3;2) і  (-4;5).
4. Чи колінеарні вектори
(-4;5).
4. Чи колінеарні вектори  (-1;2) і
(-1;2) і  (2;-4)?
5. Знайдіть скалярний добуток векторів
(2;-4)?
5. Знайдіть скалярний добуток векторів  (1;5) і
(1;5) і  (-3;-2).
6. Знайдіть скалярний добуток векторів
(-3;-2).
6. Знайдіть скалярний добуток векторів  й
й  , якщо
, якщо 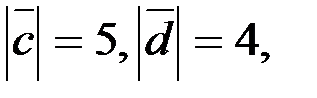 а кут між цими векторами дорівнює 300.
7. Чи перпендикулярні вектори
а кут між цими векторами дорівнює 300.
7. Чи перпендикулярні вектори
 (-2;3) і
(-2;3) і  (-1;2)?
8. Знайдіть кут між векторами
(-1;2)?
8. Знайдіть кут між векторами  (1;1) і
(1;1) і  (1;0).
9. Знайдіть косинус кута між векторами
(1;0).
9. Знайдіть косинус кута між векторами  (-3;1) і
(-3;1) і  (3;-4).
10. Вектор
(3;-4).
10. Вектор  має координати (-3;8), а точка F(5;2). Знайдіть координати точки К.
має координати (-3;8), а точка F(5;2). Знайдіть координати точки К.
 , де А(2;4), В(-3;0).
2. Знайдіть довжину вектора
, де А(2;4), В(-3;0).
2. Знайдіть довжину вектора
 (6;-8).
3. Знайдіть суму векторів
(6;-8).
3. Знайдіть суму векторів  (-4;7).
4. Чи колінеарні вектори
(-4;7).
4. Чи колінеарні вектори  (-2;4) і
(-2;4) і  (6;-5)?
5. Знайдіть скалярний добуток векторів
(6;-5)?
5. Знайдіть скалярний добуток векторів  (3;4) і
(3;4) і  (-2;1).
6. Знайдіть скалярний добуток векторів
(-2;1).
6. Знайдіть скалярний добуток векторів  й
й  , якщо
, якщо  а кут між цими векторами дорівнює 450.
7. Чи перпендикулярні вектори
а кут між цими векторами дорівнює 450.
7. Чи перпендикулярні вектори  (-3;2) і
(-3;2) і  (4;6)?
8. Знайдіть кут між векторами
(4;6)?
8. Знайдіть кут між векторами  (2;2) і
(2;2) і  (0;2).
9. Знайдіть косинус кута між векторами
(0;2).
9. Знайдіть косинус кута між векторами  (-2;1) і
(-2;1) і  (4;-3).
10. Вектор
(4;-3).
10. Вектор  має координати (-4;-3), а точка F(1;3). Знайдіть координати точки К.
має координати (-4;-3), а точка F(1;3). Знайдіть координати точки К.
 , де А(3;5), В(-3;2).
2. Знайдіть довжину вектора
, де А(3;5), В(-3;2).
2. Знайдіть довжину вектора
 (2;-4).
3. Знайдіть суму векторів
(2;-4).
3. Знайдіть суму векторів  (-4;2) і
(-4;2) і  (5;7).
4. Чи колінеарні вектори
(5;7).
4. Чи колінеарні вектори  (8;-4) і
(8;-4) і  (-2;-1)?
5.Знайдіть скалярний добуток векторів
(-2;-1)?
5.Знайдіть скалярний добуток векторів  (4;2) і
(4;2) і  (-2;1).
6. Знайдіть скалярний добуток векторів
(-2;1).
6. Знайдіть скалярний добуток векторів  й
й  , якщо
, якщо  а кут між цими векторами дорівнює 1500.
7. Чи перпендикулярні вектори
а кут між цими векторами дорівнює 1500.
7. Чи перпендикулярні вектори 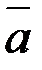 (3;2) і
(3;2) і  (-4;6)?
8. Знайдіть кут між векторами
(-4;6)?
8. Знайдіть кут між векторами
 (-1;1) і
(-1;1) і  (-1;0).
9.Знайдіть косинус кута між векторами
(-1;0).
9.Знайдіть косинус кута між векторами  (3;1) і
(3;1) і  (3;4).
10. Вектор
(3;4).
10. Вектор  має координати (2;11), а точка F(2;-3). Знайдіть координати точки К.
має координати (2;11), а точка F(2;-3). Знайдіть координати точки К.
 , де А(4;6), В(-2;4).
2. Знайдіть довжину вектора
, де А(4;6), В(-2;4).
2. Знайдіть довжину вектора
 (-8;2).
3. Знайдіть суму векторів
(-8;2).
3. Знайдіть суму векторів  (2;-6) і
(2;-6) і  (4;-8).
4. Чи колінеарні вектори
(4;-8).
4. Чи колінеарні вектори  (7;-3) і
(7;-3) і  (1;-4)?
5.Знайдіть скалярний добуток векторів
(1;-4)?
5.Знайдіть скалярний добуток векторів  (3;2) і
(3;2) і  (-4;6).
6. Знайдіть скалярний добуток векторів
(-4;6).
6. Знайдіть скалярний добуток векторів  й
й  , якщо
, якщо  а кут між цими векторами дорівнює 1350.
7. Чи перпендикулярні вектори
а кут між цими векторами дорівнює 1350.
7. Чи перпендикулярні вектори  (4;2) і
(4;2) і  (-2;1)?
8. Знайдіть кут між векторами
(-2;1)?
8. Знайдіть кут між векторами
 (-2;2) і
(-2;2) і  (0;-2).
9.Знайдіть косинус кута між векторами
(0;-2).
9.Знайдіть косинус кута між векторами  (2;1) і
(2;1) і  (4;3).
10. Вектор
(4;3).
10. Вектор  має координати (-9;10), а точки F(4;-3). Знайдіть координати точки К.
має координати (-9;10), а точки F(4;-3). Знайдіть координати точки К.



