
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные правила техники безопасности при работе в учебной лабораторииСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
СОДЕРЖАНИЕ Введение. 4 Основные правила техники безопасности при работе в учебной лаборатории. 5 Лаб.раб.№1. Изучение зависимости удельного электрического сопротивления проводников от их состава. 7 Лаб.раб.№2. Температурная зависимость электрической проводимости твердых диэлектриков. 15 Лаб.раб.№3. Исследование зависимости диэлектрической проницаемости и тангенса угла потерь от температуры.. 21 Лаб.раб.№4. Электрическая прочность диэлектриков при напряжении промышленной частоты. 40 Лаб.раб.№5. Влияние добавок кремния на магнитные свойства железа. 45 Список литературы.. 67 ВВЕДЕНИЕ
Практикум предназначен для закрепления и углубления знаний, полученных на лекциях, из чтения книг и других источников. Для полного освоения материала необходимо научиться применять теоретические знания для выполнения лабораторных работ. Для этого требуется не только помнить основные факты и теоретические положения, но и умение анализировать ситуацию, находить взаимосвязи между явлениями, вычленять наиболее важные моменты в процессе выполнения задач на практике. Подобная степень овладения материалом курса невозможна без практической самостоятельной работы на приборах. Лабораторный практикум содержит 5 работ
Лабораторная работа № 1 ИЗУЧЕНИЕ ЗАВИСИМОСТИ УДЕЛЬНОГО ЭЛЕКТРИЧЕСКОГО СОПРОТИВЛЕНИЯ ПРОВОДНИКОВ ОТ ИХ СОСТАВА Цель работы 1. Освоить методы измерения удельного электрического сопротивления металлических материалов. 2. Исследовать влияние состава сплава на величину удельного электрического сопротивления в системах Cu-Zn, Cu-Ni, Fe-Si. 3. Изучить влияние типа легирующего на величину удельного электрического сопротивления.
Теоретическая часть Удельное электрическое сопротивление - величина, обратная проводимости, характеризующей способность прохождения электрического тока (направленного движения зарядов) через материал. Проводимость (g) в общем виде может быть выражена в виде:
где n - концентрация носителей заряда в единице объема; q - заряд носителя; m - подвижность носителей заряда. В металлических материалах основным носителем заряда являются свободные электроны. Поскольку кристаллическая решетка металлов упакована плотно, то распространение электронов удобнее всего представить в виде движения электронной волны. При взаимодействии электронной волны с узлами кристаллической решетки, возникает дифракция электронной волны. При этом амплитуда исходной волны (А) разобьется на сумму амплитуд (Sаi) дифрагированных волн. Дифрагированные волны интерферируют, и образуется новая волна. В том случае, когда кристаллическая решетка правильна, ионы являются когерентными источниками дифрагированные волн, поэтому амплитуды дифрагированных волн суммируются, и, амплитуда новой волны будет равна амплитуде исходной (рис. 1,а).
Энергия волны пропорциональна квадрату ее амплитуды, таким образом, в правильной кристаллической решетке электронная волна движется без потерь, и удельное электрическое сопротивление материала с идеальной кристаллической решеткой равно нулю. Появление в кристаллической решетке ионов другого металла, отличающихся по размеру от основного приводит к смещению некоторых ионов из равновесных положений, и дифрагированные волны становятся некогерентными (рис. 1,б). При сложении некогерентных волн амплитуда результирующей волны оказывается меньше амплитуды падающей волны, в результате у металла удельное электрическое сопротивление становится отличным от нуля, а энергия рассеянной волны обращается в тепло. Аналогичным образом удельное электрическое сопротивление растет при любых искажениях кристаллической решетки, например, обусловленных тепловыми колебаниями при повышении температуры, появлением дефектов кристаллического строения и т.п. При прогнозировании свойств сплавов большую помощь оказывают диаграммы состояния сплавов. Рис. 1.2. Диаграммы состояния и зависимость свойств от состава для случаев: а), б) неограниченной растворимости компонентов в твердом состоянии; в), г) отсутствия растворимости компонентов в твердом состоянии; д), е) ограниченной растворимости компонентов в твердом состоянии.
Так, в случае, если компоненты сплава образуют твердый раствор a (рис. 2,а), при добавлении одного компонента к другому, кристаллическая решетка искажается, и удельное электросопротивление монотонно повышается. В целом, зависимость свойств от состава носит параболический характер с максимумом в точке соответствующей эквиатомному (50/50%) составу (рис. 2, б). Эта закономерность впервые была обнаружена и изучена Н.С. Курнаковым. В тех случаях, когда один из компонентов твердого раствора является переходным металлом, наблюдаются существенные изменения зависимости электросопротивления от состава сплава. Величина сопротивления при аналогичных концентрациях твердого раствора становится в несколько раз больше и максимум электросопротивления отклоняется от эквиатомного состава в сторону переходного металла. Это вызвано тем, что переходные металлы обладают не полностью заполненными внутренними электронными оболочками, которые могут захватывать свободные электроны. В результате, значительно снижается число подвижных носителей n (1) и растет электросопротивление. В том случае, когда компоненты сплава нерастворимы друг в друге (рис. 2,г), возникает сплав типа смеси зерен двух фаз, состоящих из чистых компонентов - A+B. В этом случае искажений решетки каждой из фаз не возникает, а изменение соотношения компонентов приводит лишь к увеличению объемной доли второй фазы. Для смесей зависимость удельного электросопротивления от состава носит линейный характер (рис. 2, г). Комбинированный случай представлен на рис. 2, д. Если компоненты ограниченно растворимы один в другом, то сплав, в зависимости от состава может быть твердым раствором a или b, либо смесью этих же фаз a+b. Соответственно комбинированной получается и зависимость электросопротивления от состава сплава (рис. 2, е). В некоторых случаях при сплавлении компонентов возможно появление интерметаллидных фаз - химических соединений металлов. Концентрация свободных электронов в интерметаллидном соединении понижается из-за появления ковалентной или ионной связи, что ведет к снижению электропроводности (1). Вместе с тем, интерметаллидные соединения часто имеют упорядоченную структуру, поэтому рассеяние электронной волны уменьшается и электропроводность растет.
Реальные технические сплавы обычно имеют сложное строение и состав. Например, латуни – сплавы меди с цинком, при содержании цинка до»35% представляют собой a-твердые растворы. Их сопротивление подчиняется правилу Курнакова. При большей концентрации цинка латуни состоят из смеси a+b фаз, из которых b относится к интерметаллидам, т.е. имеет пониженную концентрацию свободных электронов. При температурах ниже»450°С b-фаза приобретает упорядоченное строение и обозначается как b'. Диаграмма состояния сплавов системы Cu-Ni аналогична рис. 2,а, но зависимость сопротивления от концентрации сплава отличается от рис. 2,б, т.к. никель - переходный металл и способен захватывать свободные электроны на недостроенную 3 d -оболочку. Эти отличия следует установить в результате выполнения данной работы. Электротехнические стали – сплавы системы Fe-Si, в области применяемых составов (до 5% кремния) представляют собой твердые растворы кремния в железе. Экспериментальная часть В работе изучается зависимость удельного электрического сопротивления от состава сплавов систем Fe-Si, Cu-Ni, Cu-Zn.
RN G R1
RX RЭ
Рис. 1.4. Принципиальная схема метода двойного моста.
Изучение сопротивления сплавов системы Fe-Si осуществляется методом двойного моста (рис. 4), образованного сопротивлением исследуемого образца (RX), и резисторами R Э, R 1 и RN. Сопротивление R 1 определяется из условия баланса моста
Индикатором баланса моста служит нуль-гальванометр G. Образцы в виде пластин зажимаются в контактном приспособлении на установке. Марка, состав и геометрия пластин приведены в таблице, размещенной на установке. Сопротивление сплавов систем Cu-Ni и Cu-Zn определяется методом вольтметра-амперметра (рис. 5).
RX
Ток от стабилизированного источника проходит через последовательно соединенные эталонный резистор RЭ и исследуемый образец RX. Подключив цифровой вольтметр, с помощью переключателя П1, к RЭ, можно определить силу тока в цепи: I =UЭ/RЭ, где UЭ - показания вольтметра. В данной установке RЭ = 1±0,001 Ом. Поэтому значение силы тока будет численно равно показанию вольтметра. В противоположном положении переключателя П1 измеряется падение напряжения UX на исследуемом образце. Сопротивление образца определяют по закону Ома для участка цепи: RX = UX/I. Для исключения влияния сопротивления контактов и подводящих проводников здесь применена четырехконтактная схема подключения, которая обычно используется для измерения малых сопротивлений. Смена образцов осуществляется многопозиционным переключателем, который на схеме не показан. Состав и геометрия образцов приведены в таблице, размещенной на установке. Сплавы системы Cu-Zn - латуни - маркируются следующим образом: Л90 - латунь с содержанием меди 90 %; Л80 - латунь с содержанием меди 80 %.
При построении зависимости удельного электрического сопротивления от состава материала обратите внимание на то, что в системе Cu-Ni исследуются четыре сплава: медь марки М0, никелин Cu+30%Ni, константан Cu+40%Ni, никель промышленной чистоты. Результаты измерений занесите в таблицы 1.1 и 1.2, постройте зависимости удельного сопротивления от состава для сплавов трех систем Cu-Zn, Cu-Ni, Fe-Si.
Таблица 1.1
Таблица 1.2
Требования к отчету Отчет должен содержать: наименование работы, цель работы, краткую теоретическую часть, результаты в виде таблиц и графиков, выводы. 5. Контрольные вопросы 1. У какого материала выше удельное электрическое сопротивление: Cu+20%Zn или Ni+20%Cr? 2. Как повлияет на удельное сопротивление меди пластическая деформация? 3. У какого металла ниже удельное сопротивление железа или алюминия? 4. Как изменится удельное сопротивление алюминия при повышении температуры? 5. Как изменится удельное сопротивление железа при измельчении зерен?
Лабораторная работа №2 Цель работы 1. Ознакомиться с методом экспериментального изучения температурной зависимости электропроводности твердых диэлектриков в поле постоянного напряжения. 2. Изучить характер температурной зависимости объемного удельного электрического сопротивления. 3.Определить энергию активации электропроводности. Теоретическая часть Электрическая проводимость твердых диэлектриков в основном обусловлена перемещением ионов. В общем виде, электропроводность любых веществ можно представить в виде: g= nqm, (1) где - g - электропроводность; n - концентрация носителей заряда; q - величина заряда; m - подвижность носителя, численно равная средней скорости направленного движения заряда в электрическом поле единичной напряженности. Электропроводность диэлектриков при постоянном напряжении обусловлена диффузионной подвижностью слабо связанных ионов. Концентрация носителей заряда (подвижных ионов) зависит от энергии химической связи и от энергии теплового возбуждения. Иначе говоря, концентрация подвижных ионов зависит от физико-химической природы диэлектрика и от температуры. Зависимость потенциальной энергии иона от его положения в пространстве можно описать периодической функцией (см. рисунок 3.1). В том случае, когда энергия системы минимальна, каждый ион находится в дне потенциальной ямы, то есть в наиболее устойчивом положении. При повышении энергии системы (нагреве материала) ион приподнимается относительно дна потенциальной ямы и получает возможность колебаться относительно положения равновесия. Амплитуда колебаний определяется положением стенок потенциальной кривой. Таким образом, с ростом температуры амплитуда колебаний ионов возрастает. Обмен элементарными квантами колебаний - фонтонами - приводит к тому, что энергия какого-либо иона возрастает настолько, что ион выходит из потенциальной ямы и под действием внешнего электрического поля может перемещаться. Следовательно, при увеличении температуры вероятность появления свободных носителей заряда растёт.
Рисунок 2.1. Зависимость потенциальной энергии иона от его пространственного положения в кристаллической решетке Следует иметь в виду, что в кристаллических телах при выходе иона из узла кристаллической решетки на его месте появляется точечный дефект решетки - вакансия, а вышедший из решетки ион также искажает решетку, и появляется еще один вид точечных дефектов - межузельный атом. Такой механизм появления точечных дефектов был предложен Я. И. Френкелем. Несколько позже Шоттки оценил энергию искажения решетки вблизи вакансии и межузельного атома и пришел к выводу, что в плотноупакованных решетках образование вакансий по механизму Френкеля невозможно. Поэтому был предложен иной механизм появления вакансий: ион, лежащий на поверхности кристалла, выходит из узла кристаллической решетки, и на его месте образуется вакансия, затем следующий ион переходит на место вакансии, и вакансия перемещается в глубь кристалла. Присутствие в кристалле вакансий можно рассматривать как наличие носителей заряда, поскольку отсутствие иона в узле решетки приводит к локальному искажению плотности зарядов. Подвижность вакансий существенно больше подвижности межузельных ионов, поэтому можно рассматривать вакансии как основные носители заряда в кристаллических диэлектриках. Для образования вакансий необходимо затратить энергию, равную глубине потенциальной ямы (приблизительно 1 электрон-вольт). При росте температуры концентрация вакансий возрастает в соответствии с выражением: Сv=Co exp(Ea/kT) (2) где Сv - концентрация вакансий; Со - константа; Еа - энергия активации, kT - тепловая энергия. Важно иметь в виду, что в реальных материалах часто присутствуют примеси. Поскольку размеры иона примеси отличаются от размеров ионов основного материала, то решетка вблизи иона примеси искажена, а следовательно, энергия таких ионов повышена. Поэтому энергия активации образования вакансий снижена. Поскольку проводимость пропорциональна концентрации носителей заряда, то энергию активации можно вычислить из зависимости: g =А ехр(Еа/kT) (3) где А - константа, остальные обозначения стандартные. Прологарифмировав выражение (3), получаем: ln g =lnA+Ea/kT (4) Тогда разница логарифмов проводимости будет равна: lng1– lng2= Ea/k(T1–T2) (5) Таким образом, из линейной зависимости lng ~ (1/T) можно определить энергию активации электропроводности:
Экспериментальная часть Установка для определения температурной зависимости удельного электрического сопротивления состоит из тераомметра, нагревательной печи с двумя электродами для образцов, термопары с регулирующим потенциометром. Принципиальная схема установки для изучения температурной проводимости диэлектриков показана на рисунке 2. В качестве материала для исследования в работе использовалась конструкционная керамика на основе оксида магния. Помимо оксида магния в состав керамики входят оксиды титана, алюминия и кальция.
При выполнении работы установите ручку множителя в положение 107Ом, включите тумблер "Сеть", после пятиминутного прогрева прибора включите режим "Установка нуля", вращая ручку "уст.0 точно", установите стрелку прибора в положение "¥ ", переключением множителя установите предел измерений до получения конечных показаний на шкале прибора. Включите печь, измеряйте сопротивление образца через каждые 20°С до максимально допустимой температуры для данного образца. Рассчитайте удельное электрическое сопротивление при каждой температуре. Исходя из удельного электрического сопротивления, рассчитайте электропроводность материала g=1/r. Данные занесите в таблицу 2.1. Таблица 2.1
Постройте зависимость lng(1/T), аппроксимируйте ее отдельные участки прямыми линиями, выберите на этих линиях две произвольные точки и по их значениям вычислите энергию активации процесса. Требования к отчету Отчет должен содержать: наименование работы, цель работы, краткую теоретическую часть, результаты в виде таблиц и графиков, выводы. 5 Контрольные вопросы
1. Температура плавления оксида магния 2800 °С, температура плавления оксида висмута 820 °С. У какого оксида выше удельное электросопротивление при комнатной температуре. 2. Как повлияет добавка оксида кальция на удельное сопротивление оксида магния. 3. Как повлияет на удельное сопротивление оксида магния облучение нейтронами? 4. Оксид кремния может быть получен как в кристаллическом виде (кварц), так и в аморфном (кварцевое стекло). У какого материала выше удельное сопротивление? Лабораторная работа № 3 Цель работы 1. Ознакомиться с методами измерения диэлектрической проницаемости и тангенса угла диэлектрических потерь. 2. Экспериментально изучить температурную зависимость диэлектрической проницаемости и тангенса угла диэлектрических потерь. Теоретическая часть Диэлектрическими принято называть материалы, имеющие низкую плотность подвижных носителей заряда (ионов и электронов), поэтому удельное электрическое сопротивление таких материалов в 1012- 1025раз выше, чем у проводниковых материалов. Очевидно, что диэлектрическими являются материалы с ковалентной, поляризационной или ионной связью между атомами, причем последние только в твердом состоянии. Кроме того, энергия возбуждения электронов на уровни проводимости превосходит 5 электрон-вольт. По агрегатному состоянию диэлектрики бывают твердыми, жидкими и газообразными. По происхождению диэлектрики могут быть естественными и искусственными, органическими и неорганическими. По электрической структуре все диэлектрики можно разделить на неполярные и полярные. У неполярных диэлектриков в отсутствии внешнего поля собственный дипольный момент структурных единиц (атомов, молекул, элементарных кристаллических ячеек) равен нулю. У полярных диэлектриков собственный дипольный момент структурных единиц отличен от нуля и в отсутствии внешнего поля. В свою очередь, полярные диэлектрики могут быть параэлектрическими и сегнетоэлектрическими. У параэлектриков дипольные моменты структурных единиц распределены по разным направлениям хаотически, и суммарный дипольный момент даже небольшого объема равен нулю. У сегнетоэлектриков дипольные моменты ориентированы параллельно, и суммарный дипольный момент малых объемов не равен нулю. При помещении диэлектрика в электрическое поле в нем развиваются два основных процесса: поляризация и сквозная электропроводность. Развитие основных процессов может, в свою очередь, привести к ряду дополнительных процессов к потере энергии электрического поля в диэлектрике и пробою диэлектрика. Рассмотрим влияние внешних условий на развитие основных процессов в диэлектриках.
ПОЛЯРИЗАЦИЯ ДИЭЛЕКТРИКОВ
Поляризацией называется такое состояние диэлектрика, когда суммарный электрический момент отличен от нуля. Появление поляризации является следствием воздействия различных факторов: электрического поля, температуры, механических напряжений и др. В большинстве диэлектриков поляризация возникает под действием электрического поля, поэтому в основном мы будем рассматривать этот случай. По электрической структуре все диэлектрики можно разделить на полярные и неполярные. У полярных диэлектриков структурные единицы вещества имеет собственный дипольный момент. У неполярных диэлектриков в отсутствии внешнего поля дипольного момента нет. При помещении диэлектрика в электрическое поле диполи в полярных диэлектриках поворачиваются по полю. В неполярных диэлектриках внешнее электрическое поле приводит к смещению зарядов внутри электрически нейтральных молекул, что также приводит к появлению электрических диполей. Таким образом, внутри диэлектрика возникает собственное поле, направленное противоположно внешнему полю. В итоге напряженность внешнего поля в диэлектрике ослабевает в e0eраз. Величина дипольных моментов (m), наводимых внешним полем, пропорциональна напряженности внешнего поля: m=aE (2) где aкоэффициент пропорциональности, называемый поляризуемостью. Суммарный дипольный момент в единице объема тела V является численной характеристикой поляризации (Р)
Диэлектрическую проницаемость можно определить как отношение вектора электрического смещения D к напряженности Е внешнего поля, вызвавшего это смещение: e= Поскольку вектор электрического смещения является суперпозиций напряженности электрического смещения и поляризации: D=E+P (5) то диэлектрическую проницаемость можно выразить как: e= 1+ P/E (6) По механизму смещения заряженных частиц различают электронную, ионную и дипольную поляризацию. По характеру смещения заряженных частиц поляризация может быть упругой (безгистерезисной) и релаксационной (гистерезисной).
Упругая поляризация Упругая поляризация не связана с тепловым движением молекул. К ней относятся следующие виды поляризации: а) поляризация упругого электронного смещения; б) поляризация ионного упругого смещения; в) дипольно-упругая поляризация; г) поляризация упругого ядерного смещения. Характерным для этих видов поляризации является то, что заряженные частицы под действием поля смещаются на очень малые расстояния в пределах поля упругих сил, связывающих эти частицы с другими. В этой связи поляризацией упругого ядерного смещения в промышленных материалах можно пренебречь.
Поляризация упругого электронного смещения. Этот вид поляризации связан со смещением электронных оболочек атомов относительно ядер и имеет место во всех без исключения диэлектриках, за исключением абсолютного вакуума. Важно отметить, что у неполярных диэлектриков с ковалентной связью между атомами поляризация упругого электронного смещения является основным видом поляризации (полиэтилен, трансформаторное масло, парафин, водород) (рис. 3.3.). Дипольный момент, возникающий в атомах вследствие упругого электронного смещения, увеличивается при увеличении радиусов электронных оболочек атомов и количества электронов на них.
Поскольку общий эффект поляризации при упругой деформации электронных оболочек в электрическом поле невелик, диэлектрическая проницаемость неполярных диэлектриков мала. Так у парафина e=1,8 - 2,2; у алмаза e=2,4; у кремния - 12,5; у германия - 16,0. Поскольку в качестве диэлектрических материалов алмаз, кремний, германий не используются, а используются различные углеводороды, то типичные значения eдля диэлектриков с неполярными молекулами составляют 1,8 – 2,6. При возрастании температуры объем диэлектрика возрастает, и диэлектрическая проницаемость, в соответствии с выражением (3), уменьшается (рис. 3.4.). Особенно заметно уменьшение eпри плавлении и испарении диэлектриков, когда их объем существенно возрастает. В неполярных диэлектриках диэлектрическая проницаемость практически не зависит от частоты внешнего поля. Это связано с тем, что частота вращения электронов на орбитах велика ~1015 -1016 Гц.
Поляризация упругого ионного смещения. Этот вид поляризации вызван упругим смешением ионов из равновесных положений под действием внешнего электрического поля. Он характерен для ионных кристаллов (мрамор, поваренная соль, слюда, кварц и др.). Важно отметить, что в таких материалах, наряду с поляризацией упругого ионного смещения, присутствует и поляризация упругого электронного смещения. Типичная величина диэлектрической проницаемости составляет 5-150. Так у поваренной соли (NaCl) e=6, у корунда (Al2O3) e=10, у рутила (TiO2)e=110, у титаната кальция (CaTiO3) e=150. Из приведенных данных следует, что величина поляризации возрастает с увеличением радиусов ионов и с увеличением их зарядов.
Повышение температуры увеличивает межатомные расстояния, вследствие чего связь между отдельными ионами ослабляется, и облегчается взаимное смещение ионов под действием внешнего электрического поля. Поэтому при повышении температуры диэлектрическая проницаемость ионных кристаллов возрастает (рис. 3.5.).
Время установления этого механизма поляризации сравнимо с периодом оптических колебаний ионов в кристаллической решетки и составляет 10-12 - 10-13 с. Поэтому до частот 1012- 1013 Гц диэлектрическая проницаемость веществ с ионной связью не зависит от частоты внешнего поля.
Дипольно-упругая поляризация. Эта поляризация заключается в повороте на малый угол диполей и имеет место в полярных твердых диэлектриках, где диполи прочно связаны связями с другими молекулами. Время установления этой поляризации составляет 10-12 – 10-13с. Поляризация упругого ядерного смещения. Этот вид поляризации наблюдается в газах со сложными молекулами. Время установления 10-12 – 10-13 с. Вклад этой поляризации в диэлектрическую проницаемость пренебрежимо мал. Экспериментальная часть Материал представляет собой твёрдый диэлектрик прямоугольной формы, с размерами 10 Х 10 мм и толщиной 0,2 мм. На две сторон пластины нанесено металлическое напыление, от которых сделаны два металлических вывода. Таким образом, образуется плоский конденсатор, ёмкость которого зависит от геометрических размеров и от свойств диэлектрика, т. е. от диэлектрической проницаемости материала (e). Измерив ёмкость конденсатора мы можем определить диэлектрическую проницаемость взятого диэлектрика, т.к. Сх = e×Со где Сх – ёмкость конденсатора, которая измеряется экспериментально, Со – ёмкость конденсатора без диэлектрика в вакууме, которую можно рассчитать по формуле: Со = εо. S/d где d – толщина пластины, S – площадь пластины. Откуда получаем: e = × Сх / Со
Емкость конденсатора при каждой температуре находится при помощи измерителя иммитанса Е7-21. Нагрев осуществляется с помощью печи, с регулируемой мощностью нагрева.
Выполнение работы 1.Включите две спирали нагревательной печи, для равномерного нагрева. Регулятор скорости нагрева должен находиться в крайнем левом положении. 2. Включите измеритель иммитанса на задней панели прибора. На индикаторной панели измерителя верхняя строка показывает ёмкость (нФ), нижняя левая - тангенс угла потерь, нижняя правая - частоту, при которой проводятся измерения. 3. Через 2 минуты после прогрева прибора запишите показания при комнатной температуре. 4.Плавно поворачивайте регулятор скорости нагрева. Индикаторная лампа на передней панели печи показывает интенсивность нагрева. Остановившись на определённом положении регулятора, подождите 2 – 3 минуты, для того чтобы температура печи установилась. После этого записывайте значения. Внимательно следите за температурой, проводя измерения через каждые 10 градусов. Измерения снимаются при нагреве до 140о.
ВНИМАНИЕ: Не поворачивайте регулятор скорости нагрева слишком резко, чтобы температура в печи не превысила 140о.
После достижения предельной температуры регулятор скорости нагрева уберите в крайнее левое положение и полностью выключите нагревательный прибор.
ПРЕДУПРЕЖДЕНИЕ: автоматический цифровой измеритель иммитанса - сложный дорогостоящий прибор, требующий аккуратного обращения. Не проводите манипуляций с прибором, не предусмотренных настоящим описанием.
5.Рассчитайте значения диэлектрической проницаемости материала при каждой температуре. 6.Занесите данные в таблицу 5.1. Таблица 5.1
7.Постройте графики зависимости тангенса угла потерь и диэлектрической проницаемости от температуры и объясните их. 8.По результатам измерений определите предполагаемый механизм поляризации материала (электронный, ионный и т.д.). Требования к отчету Отчет должен содержать: наименование работы, цель работы, краткую теоретическую часть, результаты в виде таблиц и графиков, выводы.
Контрольные вопросы
Лабораторная работа № 4 Цель работы Освоить метод экспериментального определения электрической прочности диэлектриков. Теоретическая часть Электрической прочностью диэлектрика называют ту напряженность поля, при которой диэлектрик теряет изоляционные свойства. Поскольку напряженность определяют как градиент потенциала, то электрическую прочность (Епр) можно оценить как отношение напряжения, приводящего к пробою (Uпр), к толщине диэлектрика (d). Епр=Uпр/d (1) Boзможно развитие трех механизмов пробоя: электрического, электротеплового и электрохимического. Механизм пробоя зависит от напряженности поля, температуры материала, его толщины, условий охлаждения, воздействия с окружающей среды. В газах обычно развивается электрический пробой. Рассмотрим пробой воздуха. В воздухе всегда содержится небольшое количество ионов, образующихся за счет действия космических лучей, естественной радиоактивности земли и других факторов. Под воздействием электрического поля ионы ускоряются и на длине свободного пробега набирают кинетическую энергию (Wк): Wк= qlE (2) где q - заряд частицы; l - длина свободного пробега в направлении поля (расстояние между двумя столкновениями с молекулами); Е - напряженность электрического поля. Сталкиваясь с молекулой, ион передает ей энергию. Если эта энергия превышает энергию ионизации (Wи), то происходит ударная ионизация с образованием свободного электрона и положительно заряженного иона. Условие возникновения ударной ионизации можно записать в виде: Wк>Wи. Отсюда можно оценить минимальную напряженность поля, при которой начинается ударная ионизация: Еи= Wи/ql (3) Помимо ударной ионизации, возможна фотонная ионизация газов при существенно меньших значениях напряженности поля. В этом случае взаимодействие иона с молекулой не приводит к ее ионизации, поскольку кинетическая энергия иона меньше энергии ионизации. Однако, поглотив кинетическую энергию иона, молекула переходит в возбужденное состояние. При переходе молекулы в равновесное состояние она испускает квант электромагнитного поля - фотон. В случае, если несколько фотонов одновременно попадет на какую-либо молекулу, суммарная энергия поглощенная молекулой, окажется больше энергии ионизации, что станет причиной образования дополнительной пары ионов. Очевидно, что повышение объема газа приведет к увеличению вероятности попадания нескольких фотонов в одну и ту же молекулу, поскольку возрастает общее количество ионов и, соответственно, увеличивается генерация фотонов. В газах длина с
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-09; просмотров: 428; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.233.69 (0.013 с.) |

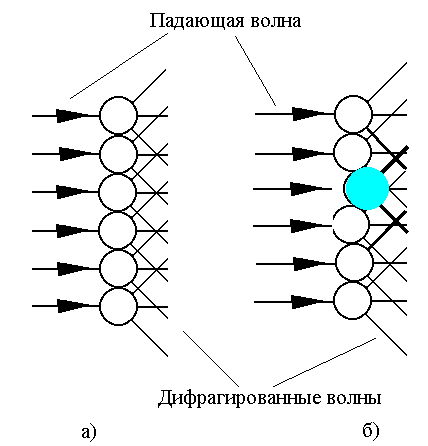
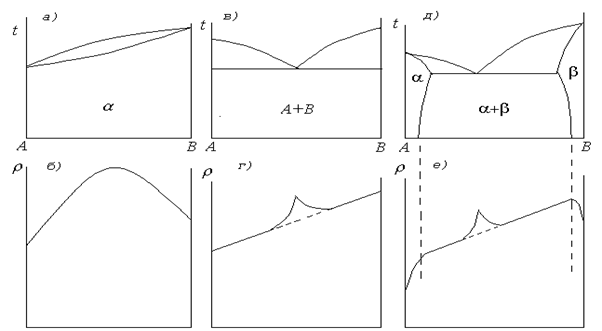
 Рис. 1.3. Фрагмент диаграммы состояния сплавов медь-цинк.
Рис. 1.3. Фрагмент диаграммы состояния сплавов медь-цинк.

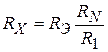 .
. RЭ
RЭ

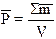 (3)
(3) (4)
(4)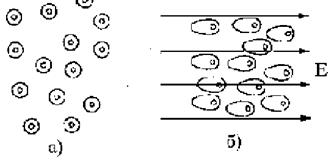 Рис. 3.3. Деформация симметричных электронных оболочек атомов и образование диполей при наличии электрического поля. а) симметричные электронные оболочки атомов при отсутствии электрического поля; б) деформированные электронные оболочки атомов при наличии внешнего поля напряженностью Е.
Рис. 3.3. Деформация симметричных электронных оболочек атомов и образование диполей при наличии электрического поля. а) симметричные электронные оболочки атомов при отсутствии электрического поля; б) деформированные электронные оболочки атомов при наличии внешнего поля напряженностью Е.
 Рис. 3.4. Зависимость диэлектрической проницаемости от температуры для неполярных диэлектриков.
Рис. 3.4. Зависимость диэлектрической проницаемости от температуры для неполярных диэлектриков.

 Рис. 3.5. Зависимость диэлектрической проницаемости от температуры для ионных кристаллов.
Рис. 3.5. Зависимость диэлектрической проницаемости от температуры для ионных кристаллов.



