
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Изучение зависимости удельного электрического сопротивления проводников от их составаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Цель работы 1. Освоить методы измерения удельного электрического сопротивления металлических материалов. 2. Исследовать влияние состава сплава на величину удельного электрического сопротивления в системах Cu-Zn, Cu-Ni, Fe-Si. 3. Изучить влияние типа легирующего на величину удельного электрического сопротивления.
Теоретическая часть Удельное электрическое сопротивление - величина, обратная проводимости, характеризующей способность прохождения электрического тока (направленного движения зарядов) через материал. Проводимость (g) в общем виде может быть выражена в виде:
где n - концентрация носителей заряда в единице объема; q - заряд носителя; m - подвижность носителей заряда. В металлических материалах основным носителем заряда являются свободные электроны. Поскольку кристаллическая решетка металлов упакована плотно, то распространение электронов удобнее всего представить в виде движения электронной волны. При взаимодействии электронной волны с узлами кристаллической решетки, возникает дифракция электронной волны. При этом амплитуда исходной волны (А) разобьется на сумму амплитуд (Sаi) дифрагированных волн. Дифрагированные волны интерферируют, и образуется новая волна. В том случае, когда кристаллическая решетка правильна, ионы являются когерентными источниками дифрагированные волн, поэтому амплитуды дифрагированных волн суммируются, и, амплитуда новой волны будет равна амплитуде исходной (рис. 1,а).
Энергия волны пропорциональна квадрату ее амплитуды, таким образом, в правильной кристаллической решетке электронная волна движется без потерь, и удельное электрическое сопротивление материала с идеальной кристаллической решеткой равно нулю. Появление в кристаллической решетке ионов другого металла, отличающихся по размеру от основного приводит к смещению некоторых ионов из равновесных положений, и дифрагированные волны становятся некогерентными (рис. 1,б). При сложении некогерентных волн амплитуда результирующей волны оказывается меньше амплитуды падающей волны, в результате у металла удельное электрическое сопротивление становится отличным от нуля, а энергия рассеянной волны обращается в тепло. Аналогичным образом удельное электрическое сопротивление растет при любых искажениях кристаллической решетки, например, обусловленных тепловыми колебаниями при повышении температуры, появлением дефектов кристаллического строения и т.п. При прогнозировании свойств сплавов большую помощь оказывают диаграммы состояния сплавов. Рис. 1.2. Диаграммы состояния и зависимость свойств от состава для случаев: а), б) неограниченной растворимости компонентов в твердом состоянии; в), г) отсутствия растворимости компонентов в твердом состоянии; д), е) ограниченной растворимости компонентов в твердом состоянии.
Так, в случае, если компоненты сплава образуют твердый раствор a (рис. 2,а), при добавлении одного компонента к другому, кристаллическая решетка искажается, и удельное электросопротивление монотонно повышается. В целом, зависимость свойств от состава носит параболический характер с максимумом в точке соответствующей эквиатомному (50/50%) составу (рис. 2, б). Эта закономерность впервые была обнаружена и изучена Н.С. Курнаковым. В тех случаях, когда один из компонентов твердого раствора является переходным металлом, наблюдаются существенные изменения зависимости электросопротивления от состава сплава. Величина сопротивления при аналогичных концентрациях твердого раствора становится в несколько раз больше и максимум электросопротивления отклоняется от эквиатомного состава в сторону переходного металла. Это вызвано тем, что переходные металлы обладают не полностью заполненными внутренними электронными оболочками, которые могут захватывать свободные электроны. В результате, значительно снижается число подвижных носителей n (1) и растет электросопротивление. В том случае, когда компоненты сплава нерастворимы друг в друге (рис. 2,г), возникает сплав типа смеси зерен двух фаз, состоящих из чистых компонентов - A+B. В этом случае искажений решетки каждой из фаз не возникает, а изменение соотношения компонентов приводит лишь к увеличению объемной доли второй фазы. Для смесей зависимость удельного электросопротивления от состава носит линейный характер (рис. 2, г). Комбинированный случай представлен на рис. 2, д. Если компоненты ограниченно растворимы один в другом, то сплав, в зависимости от состава может быть твердым раствором a или b, либо смесью этих же фаз a+b. Соответственно комбинированной получается и зависимость электросопротивления от состава сплава (рис. 2, е). В некоторых случаях при сплавлении компонентов возможно появление интерметаллидных фаз - химических соединений металлов. Концентрация свободных электронов в интерметаллидном соединении понижается из-за появления ковалентной или ионной связи, что ведет к снижению электропроводности (1). Вместе с тем, интерметаллидные соединения часто имеют упорядоченную структуру, поэтому рассеяние электронной волны уменьшается и электропроводность растет.
Реальные технические сплавы обычно имеют сложное строение и состав. Например, латуни – сплавы меди с цинком, при содержании цинка до»35% представляют собой a-твердые растворы. Их сопротивление подчиняется правилу Курнакова. При большей концентрации цинка латуни состоят из смеси a+b фаз, из которых b относится к интерметаллидам, т.е. имеет пониженную концентрацию свободных электронов. При температурах ниже»450°С b-фаза приобретает упорядоченное строение и обозначается как b'. Диаграмма состояния сплавов системы Cu-Ni аналогична рис. 2,а, но зависимость сопротивления от концентрации сплава отличается от рис. 2,б, т.к. никель - переходный металл и способен захватывать свободные электроны на недостроенную 3 d -оболочку. Эти отличия следует установить в результате выполнения данной работы. Электротехнические стали – сплавы системы Fe-Si, в области применяемых составов (до 5% кремния) представляют собой твердые растворы кремния в железе. Экспериментальная часть В работе изучается зависимость удельного электрического сопротивления от состава сплавов систем Fe-Si, Cu-Ni, Cu-Zn.
RN G R1
RX RЭ
Рис. 1.4. Принципиальная схема метода двойного моста.
Изучение сопротивления сплавов системы Fe-Si осуществляется методом двойного моста (рис. 4), образованного сопротивлением исследуемого образца (RX), и резисторами R Э, R 1 и RN. Сопротивление R 1 определяется из условия баланса моста
Индикатором баланса моста служит нуль-гальванометр G. Образцы в виде пластин зажимаются в контактном приспособлении на установке. Марка, состав и геометрия пластин приведены в таблице, размещенной на установке. Сопротивление сплавов систем Cu-Ni и Cu-Zn определяется методом вольтметра-амперметра (рис. 5).
RX
Ток от стабилизированного источника проходит через последовательно соединенные эталонный резистор RЭ и исследуемый образец RX. Подключив цифровой вольтметр, с помощью переключателя П1, к RЭ, можно определить силу тока в цепи: I =UЭ/RЭ, где UЭ - показания вольтметра. В данной установке RЭ = 1±0,001 Ом. Поэтому значение силы тока будет численно равно показанию вольтметра. В противоположном положении переключателя П1 измеряется падение напряжения UX на исследуемом образце. Сопротивление образца определяют по закону Ома для участка цепи: RX = UX/I. Для исключения влияния сопротивления контактов и подводящих проводников здесь применена четырехконтактная схема подключения, которая обычно используется для измерения малых сопротивлений. Смена образцов осуществляется многопозиционным переключателем, который на схеме не показан. Состав и геометрия образцов приведены в таблице, размещенной на установке. Сплавы системы Cu-Zn - латуни - маркируются следующим образом: Л90 - латунь с содержанием меди 90 %; Л80 - латунь с содержанием меди 80 %.
При построении зависимости удельного электрического сопротивления от состава материала обратите внимание на то, что в системе Cu-Ni исследуются четыре сплава: медь марки М0, никелин Cu+30%Ni, константан Cu+40%Ni, никель промышленной чистоты. Результаты измерений занесите в таблицы 1.1 и 1.2, постройте зависимости удельного сопротивления от состава для сплавов трех систем Cu-Zn, Cu-Ni, Fe-Si.
Таблица 1.1
Таблица 1.2
Требования к отчету Отчет должен содержать: наименование работы, цель работы, краткую теоретическую часть, результаты в виде таблиц и графиков, выводы. 5. Контрольные вопросы 1. У какого материала выше удельное электрическое сопротивление: Cu+20%Zn или Ni+20%Cr? 2. Как повлияет на удельное сопротивление меди пластическая деформация? 3. У какого металла ниже удельное сопротивление железа или алюминия? 4. Как изменится удельное сопротивление алюминия при повышении температуры? 5. Как изменится удельное сопротивление железа при измельчении зерен?
Лабораторная работа №2
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-09; просмотров: 1030; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.008 с.) |

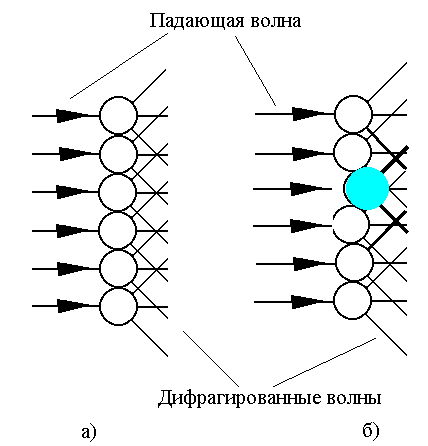
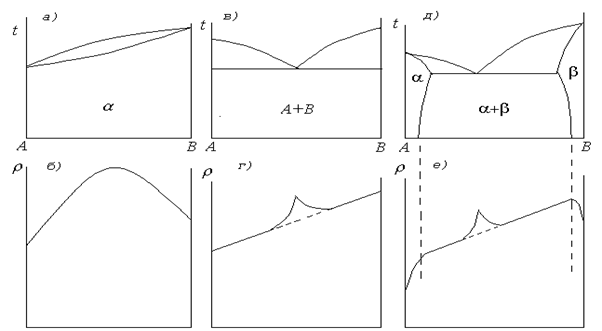
 Рис. 1.3. Фрагмент диаграммы состояния сплавов медь-цинк.
Рис. 1.3. Фрагмент диаграммы состояния сплавов медь-цинк.

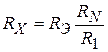 .
. RЭ
RЭ


