
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Внутренние и внешние силы. Главный вектор и главный момент внутренних сил. Метод сечений.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Внутри любого материала имеются внутренние межатомные силы, наличие которых определяет способность тела воспринимать действующие на него внешние силы, сопротивляться разрушению, изменению формы и размеров. Под внутренними силами в сопротивлении материалов понимаются силы между отдельными элементами конструкции или между отдельными частями элемента, возникающие под действием внешних сил. Внешняя сила — это мера взаимодействия между телами. В задачах сопротивления материалов внешние силы считаются всегда заданными. К внешним силам относятся также реакции опор. Рассмотрим плоскую систему сил (F 1, F 2,..., F n),действующих на твердое тело в координатной плоскости Oxy. Главным вектором системы сил называется вектор R, равный векторной сумме этих сил: R = F 1 + F 2 +... + F n = Для плоской системы сил ее главный вектор лежит в плоскости действия этих сил. Главным моментом системы сил относительно центра O называется вектор L O, равный сумме векторных моментов этих сил относительно точки О: L O = M O(F 1) + M O(F 2) +... + M O(F n) =
Метод сечений: Операции РОЗУ: 1)Разрезаем брус на две части 2)Отбрасываем одну из частей 3)Заменяем действие отброшенной части на оставленную часть шестью внутренними силовыми факторами 4)Уравновешиваем внешние силы оставленной части внутренними силовыми факторами. Напряжения.
В окрестности точки М выделим элементарную площадку ∆А. Главный вектор действующих сил, действующий на площадку – ∆R
τ–касательное напряжение σ–нормальное напряжение
Перемещения и деформации. Изменение линейных размеров тела или его частей называется линейной деформацией, а изменение угловых размеров – угловой деформацией.
Изменение взаимного положения точек до и после деформации
Деформации вызывают изменение размеров и формы тела. В результате этого точки тела перемещаются в новые положения, а элементарные отрезки поворачиваются.
Закон Гука и принцип независимости действия сил. Перемещения в определенных пределах пропорциональны действующим силам. Закон Гука определяет линейную зависимость между напряжением и деформацией: -при линейной деформации: σ=Еε, Е–модуль упругости первого рода -при угловой деформации: τ=Gγ, G–модуль упругости второго рода, Принцип независимости действия сил утверждает, что в упругой системе напряжения и деформации от действия одной нагрузки не зависят от наличия или отсутствия других нагрузок. Важным следствием является утверждение, что результат действия суммы сил не зависит от порядка их приложения. Из принципа также вытекает, что действие суммы сил равно сумме действий каждой силы в отдельности.
Внутренние силы и напряжения при растяжении-сжатии. Растяжение(сжатие)–такой вид нагружения, при котором в поперечных сечениях стержня возникают только нормальные силы N, а все остальные внутренние силовые факторы равны нулю.
Нормальная сила N, возникающая в поперечном сечении стержня, представляет собой равнодействующую внутренних нормальных сил, распределенных по площади поперечного сечения, и связана с возникающими в этом сечении нормальными напряжениями зависимостью Длина всех продольных волокон, расположенных между любыми двумя поперечными сечениями, в процессе растяжения(сжатия) изменяется одинаково. Следовательно одинаковой у всех волокон оказывается и величина относительной линейной деформации, и напряженность этих волокон
|
||||
|
Последнее изменение этой страницы: 2016-09-18; просмотров: 1858; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.83.202 (0.007 с.) |

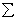 F i.
F i.
 Распределение внутренних усилий по сечению заранее не известно. Чтобы характеризовать закон распределения внутренних сил по сечению, необходимо ввести для них числовую меру. За такую меру принимается напряжение.
Распределение внутренних усилий по сечению заранее не известно. Чтобы характеризовать закон распределения внутренних сил по сечению, необходимо ввести для них числовую меру. За такую меру принимается напряжение.
 – среднее напряжение на данной площадке.
– среднее напряжение на данной площадке.



 Если воспользоваться методом сечений, то становиться очевидным, что во всех поперечных сечениях стержня возникают нормальные силы N, равные силе F.
Если воспользоваться методом сечений, то становиться очевидным, что во всех поперечных сечениях стержня возникают нормальные силы N, равные силе F. – элементарная внутренняя сила, приходящаяся на площадку dA
– элементарная внутренняя сила, приходящаяся на площадку dA . Следовательно,
. Следовательно, 



