
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Обусловленную влиянием прочих факторов по совокупности в целомСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Дисперсия альтернативного признака определяется по формуле:
+
Выработка рабочих двух бригад за семь дней: Первая бригада: 4,4,5,5,5,6,6; средняя выработка 5 шт Вторая бригада: 1,2,2,2,7,10,11; средняя выработка 5 шт Более равномерно работала бригада: Первая вторая обе
Для получения равных интервалов необходимо поделить на количество групп: среднее квадратическое отклонение дисперсию Размах вариации среднее линейное отклонение
Коэффициент вариации является показателем вариации: абсолютным Относительным средним
Если коэффициент вариации составляет 25%, то совокупность: умеренно однородная средней однородности Однородная неоднородная
Согласно правилу общая дисперсия равна… межгрупповой дисперсии и средней из внутригрупповых дисперсий: Сумме частному разности произведению
Уровень однородности статистической совокупности определяется значением: среднего квадратического отклонения размаха вариации Коэффициента вариации дисперсии
Тема 5. Выборочное наблюдение
σ2 ∆ ∆2 (N-1)
σ2 ∆ +∆2 (N-1)
σ2 ∆ ∆2 (N-1)
Репрезентативность результатов выборочного наблюдения зависит от Вариации признака и объема выборки определения границ объекта исследования времени проведения наблюдения продолжительности проведения наблюдения
наличии высокого уровня вариации признака изучении качественных характеристик явлений Малой выборке уточнении данных сплошного наблюдения
Cредняя ошибка случайной повторной выборки..., если ее объем увеличить в 4 раза Уменьшится в 2 раза увеличится в 4 раза уменьшится в 4 раза не изменится
t t2 n2 n N
вариацию признака тес ноту связи между двумя факторами Среднюю величину всех возможных расхождений выборочной и генеральной средней Среднее значение признака темп роста
Под выборочным наблюдением понимают: сплошное наблюдение всех единиц совокупности несплошное наблюдение части единиц совокупности Несплошное наблюдение части единиц совокупности, отобранных случайным способом наблюдение за единицами совокупности в определенные моменты времени обследование наиболее крупных единиц изучаемой совокупности
Недостающим элементом в формуле дисперсии доли для генеральной совокупности является р m M W
Пропорция отбора в выборочную совокупность при механической выборке определяется: Соотношением объемов выборочной и генеральной совокупностей уровнем вероятности методом отбора
Способ собственно-случайного отбора в выборочную совокупность заключается в отборе из генеральной совокупности: каждой десятой единицы совокупности Без какой либо системности в зависимости от уровня вероятности
Необходимая численность серийной выборки при бесповторном отборе определяется по формуле:
+
Для оценки результатов малой выборки пользуются: критерием Фишера Критерием Стъюдента ничем не пользуются
Недостающим элементов в формуле предельной ошибки выборки для доли при бесповторном отборе является: n N W σ
Для получения предельной ошибки выборки необходимо умножить среднюю ошибку выборки на: Коэффициент доверия численность выборочной совокупности численность генеральной совокупности
По формуле средняя повторная Средняя бесповторная предельная повторная предельная бесповторная
При случайном бесповторном отборе средняя ошибка выборки определяется по формуле:
+
Выборка называется малой, если ее объем составляет менее: 40 единиц Единиц 100 единиц 150 единиц
Выборка заключающаяся в отборе единиц из общего списка единиц генеральной совокупности через равные интервалы в соответствии с установленным процентом отбора называется: типической Механической случайной повторной
Для использования выборочной совокупности для дальнейшего анализа развития социально-экономического явления необходимо, чтобы разница между средним значением генеральной совокупности и средним значением выборочной совокупности была не более ошибки выборки: средней индивидуальной Предельной генеральной
|
||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 683; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.247.237 (0.011 с.) |





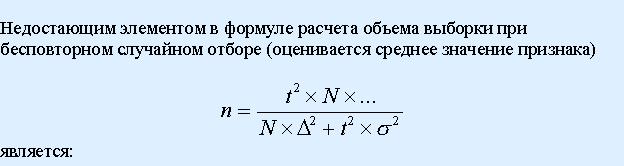


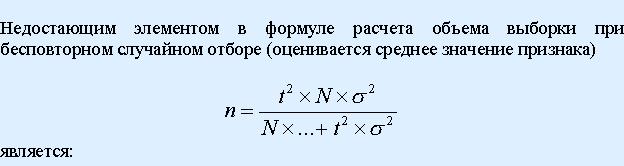




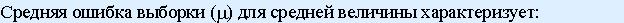





 определяется ошибка выборки:
определяется ошибка выборки:





