
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
По формулам (2. 9), (2. 10) определяются наибольшие и наименьшие зазоры для соединений по внутреннему диаметру d, наружному диаметру d и ширине B.Содержание книги
Поиск на нашем сайте
Пример расчета посадки с натягом приведен в приложении Р.
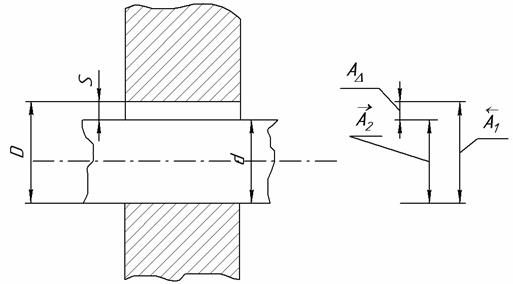
Решение задач теории размерных цепей Общие сведения о размерных цепях Размерной цепью называют совокупность взаимосвязанных размеров, образующих замкнутый контур, непосредственно участвующих в решении поставленной задачи, а так же определяющих взаимное расположение поверхностей одной или нескольких деталей (ГОСТ 16319-80). Размерные цепи могут быть конструкторские, технологические и измерительные. Теоретические вопросы по видам цепей подробно рассмотрены в [26]. Размеры, составляющие размерную цепь, называют звеньями. На рисунке 8.1, звеньями являются диаметры d, D, S, а на рисунке 8.2 а, звеньями являются размеры, параллельные оси вала - А1, А2, А3, А4 и АD. В размерную цепь могут входить размеры любого типа: линейные размеры - диаметральные, осевые, расстояния между осями, поверхностями, зазоры, натяги, отклонения формы и отклонения расположения поверхностей и т.п.; угловые размеры - углы между плоскостями, осями, между осью и плоскостью и т.п.
а - посадка с зазором; б - размерная схема цепи
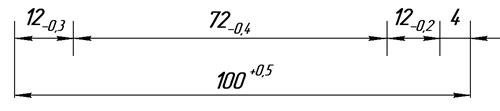
Рисунок 8.1 - Размерная цепь в посадке с зазором Звенья размерной цепи подразделяют на составляющие звенья и на замыкающее звено (исходное). Замыкающее звено - это звено, которое при сборке является последним или изготовляется последним. При расчёте размерной цепи к этому звену предъявляются основные требования в отношении точности данной сборки или данной детали. Остальные звенья, составляющие цепь, по своему влиянию, оказываемому на замыкающее звено, делятся на увеличивающие и на уменьшающие. Увеличивающие - это звенья, при увеличении которых увеличивается и замыкающее звено. Уменьшающие - это звенья, при увеличении которых уменьшается замыкающее звено. Например, на рисунке 8.2азвенья А1, А2 и А3являются уменьшающими, так как при их увеличении замыкающий цепь зазор АD уменьшится, а звено А4 является увеличивающим, так как при его увеличении увеличится и замыкающий цепь зазор - звено АD. Для удобства рассмотрения схем размерных цепей над буквами А ставят стрелки разного направления: над увеличивающими размерами стрелка направлена вправо, а над уменьшающими - влево.
Расчет размерных цепей При решении размерных цепей различают две задачи: 1 Необходимо определить номинальный размер, допуск и предельные отклонения замыкающего звена по известным номинальным размерам и предельным отклонениям составляющих звеньев. Эту задачу называют обратной и часто применяют для проверочных расчетов. Она имеет однозначное и довольно простое решение. 2 Необходимо определить допуск и предельные отклонения всех составляющих звеньев по известным номинальным размерам звеньев, допуску и предельным отклонениям замыкающего звена. Эту задачу называют прямой. Она достаточно сложна и имеет несколько решений. Размерные цепи могут решаться методами, дающими различные по точности результаты.
а)
б)
в)
а - фрагмент коробки передач; б - схема размерной цепи; в - размеры звеньев цепи
Рисунок 8.2 - Размерная цепь в коробке передач
Так в РД 50-635-87 «Цепи размерные. Основные понятия. Методы расчета линейных и угловых цепей» предусмотрены следующие методы: полной взаимозаменяемости (на максимум – минимум); неполной взаимозаменяемости (с использованием положений теории вероятностей); групповой взаимозаменяемости; метод пригонки; метод регулирования.
8.2.1 Основные расчетные формулы:
В расчетных формулах приняты следующие условные обозначения [32]:
n – количество увеличивающих звеньев; р – количество уменьшающих звеньев; m – 1 – общее количество составляющих звеньев: n+p=m-1 m – количество звеньев размерной цепи;
l - относительное среднее квадратическое отклонение;
N - число ступеней размеров неподвижного компенсатора; p - процент риска. Номинальный размер замыкающего звена размерной цепи А определяют по формуле [32]:
где j=1,2,…,m – порядковый номер звена размерной цепи
В зависимости от вида размерной цепи передаточное отношение может иметь различное содержание и значение. Так, например, для линейных размерных цепей (цепей с параллельными звеньями) передаточные отношения равны:
Поэтому для линейных размерных цепей зависимость (8.1) записывают в виде [4, 27, 33]:
где n – количество увеличивающих звеньев; p – количество уменьшающих звеньев. Допуск замыкающего звена ТАD при расчете на максимум – минимум находятся по формуле [32]:
Координату середины поля допуска
Предельные отклонения замыкающего звена АD определяют:
Возможно определение предельных отклонений замыкающего звена по зависимостям [4, 5]:
Предельные размеры замыкающего звена
При расчете вероятностным методом допуск замыкающего звена находят по формуле [32]:
где tD - коэффициент риска, принимаемый из таблицы 8.1.
Таблица 8.1 – Значения коэффициентов риска [26]
Для размерных цепей с параллельными звеньями (линейные размерные цепи) Коэффициент При распределении отклонений по закону треугольника (закон Симпсона) При распределении отклонений по закону равной вероятности Иногда в расчетах размерных цепей используют коэффициент относительного рассеяния При наиболее часто используемом проценте риска 0,27 имеем по таблице 8.1:
При использовании коэффициента относительного рассеяния формула (8.11) принимает более простой вид для линейных размерных цепей при проценте риска 0,27.
Среднее значение допуска составляющих звеньев вычисляют по формулам [55]: - при расчете по способу максимума-минимума
- при расчете вероятностным способом
Для линейных размерных цепей формулы (8.13) и (8.14) приобретают более простой вид при решении способом равных допусков [4]: - при расчете на максимум-минимум
- при расчете вероятностным методом
Решая размерную цепь способом одного квалитета, определяют число единиц допуска в допуске размера (коэффициент точности) [4]: - при полной взаимозаменяемости (на максимум-минимум)
- при неполной взаимозаменяемости (вероятностный расчет)
При решении размерной цепи методом компенсации вычисляют наибольшую возможную компенсацию VK по формуле [32]:
где Число ступеней неподвижных компенсаторов N рассчитывают по формуле [32]:
где Примеры расчета размерных цепей приведены в приложении С.
|
|||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 338; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.112.208 (0.01 с.) |



 - обозначение и номинальный размер звеньев размерной цепи А;
- обозначение и номинальный размер звеньев размерной цепи А; -обозначение и номинальный размер замыкающего звена размерной цепи А;
-обозначение и номинальный размер замыкающего звена размерной цепи А; - увеличивающее j-е составляющее звено размерной цепи А;
- увеличивающее j-е составляющее звено размерной цепи А;
 - компенсирующее j-е составляющее звено размерной цепи А;
- компенсирующее j-е составляющее звено размерной цепи А;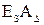 - верхнее предельное отклонение замыкающего звена размерной цепи А;
- верхнее предельное отклонение замыкающего звена размерной цепи А; - нижнее предельное отклонение замыкающего звена размерной цепи А;
- нижнее предельное отклонение замыкающего звена размерной цепи А;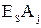 - нижнее предельное отклонение составляющего звена размерной цепи А;
- нижнее предельное отклонение составляющего звена размерной цепи А; - верхнее предельное отклонение составляющего звена размерной цепи А;
- верхнее предельное отклонение составляющего звена размерной цепи А;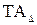 - допуск замыкающего звена размерной цепи А;
- допуск замыкающего звена размерной цепи А; - допуск j-ого звена размерной цепи А;
- допуск j-ого звена размерной цепи А; - координата середины поля допуска замыкающего звена размерной цепи А;
- координата середины поля допуска замыкающего звена размерной цепи А;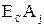 - координата середины поля допуска j-го составляющего звена размерной цепи А;
- координата середины поля допуска j-го составляющего звена размерной цепи А; - координата середины поля рассеяния замыкающего звена размерной цепи А;
- координата середины поля рассеяния замыкающего звена размерной цепи А; - координата середины поля рассеяния j-го составляющего звена размерной цепи А;
- координата середины поля рассеяния j-го составляющего звена размерной цепи А;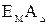 - координата центра группирования замыкающего звена размерной цепи А;
- координата центра группирования замыкающего звена размерной цепи А; - координата центра группирования j-го составляющего звена размерной цепи А;
- координата центра группирования j-го составляющего звена размерной цепи А; - величина компенсации;
- величина компенсации; - коэффициент риска;
- коэффициент риска; - коэффициент относительной ассиметрии;
- коэффициент относительной ассиметрии;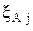 - передаточное отношение j-го звена размерной цепи А;
- передаточное отношение j-го звена размерной цепи А;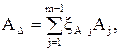 (8.1)
(8.1) - передаточное отношение j-го звена размерной цепи А.
- передаточное отношение j-го звена размерной цепи А.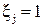 для увеличивающих составляющих звеньев;
для увеличивающих составляющих звеньев; и для уменьшающих составляющих звеньев.
и для уменьшающих составляющих звеньев. (8.2)
(8.2)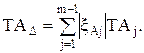 (8.3)
(8.3) замыкающего звена размерной цепи А вычисляют по зависимости [32]:
замыкающего звена размерной цепи А вычисляют по зависимости [32]: (8.4)
(8.4)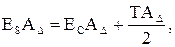 (8.5)
(8.5) (8.6)
(8.6)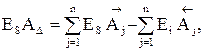 (8.7)
(8.7)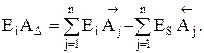 (8.8)
(8.8) (8.9)
(8.9) (8.10)
(8.10)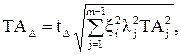 (8.11)
(8.11)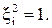
 при нормальном законе распределении отклонений (закон Гаусса).
при нормальном законе распределении отклонений (закон Гаусса).

 [27].
[27]. и с учетом значений коэффициента
и с учетом значений коэффициента  ; коэффициент относительного рассеяния
; коэффициент относительного рассеяния  составляет:
составляет: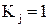 при законе распределения Гаусса;
при законе распределения Гаусса;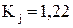 при законе распределения Симпсона;
при законе распределения Симпсона; при законе распределения равной вероятности.
при законе распределения равной вероятности. (8.12)
(8.12) (8.13)
(8.13)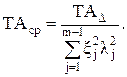 (8.14)
(8.14) (8.15)
(8.15) (8.16)
(8.16) (8.17)
(8.17) (8.18)
(8.18) (8.19)
(8.19) - производственный допуск замыкающего звена, равный сумме расширенных допусков звеньев размерной цепи.
- производственный допуск замыкающего звена, равный сумме расширенных допусков звеньев размерной цепи. (8.20)
(8.20)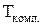 – допуск на изготовление неподвижного компенсатора.
– допуск на изготовление неподвижного компенсатора.


