
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дайте описание того что вы понимаете под анализом разделимости.Содержание книги
Поиск на нашем сайте
61. Геометрическое трансформирование изображения, линейные и нелинейные преобразования. Геометрическое трансформирование предполагает, что после его применения, мы сможем точно определяет линейные и площадные размеры объектов по снимку.
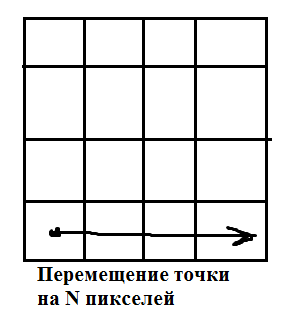
Для того чтобы транспонировать снимок в системе координат картографической проекции необходимо выполнить 2 операции: пространственная интерполяция, интерполяция значений яркости. Пространственная интерполяция выполняется по большому числу наземных опорных точек. В общем случае геометрическое трансформирование описывается полиномиальным преобразованием в частном случае аффинное преобразование (трансформация происходит с применением 6 независимых параметров: смещение вдоль оси х,у изменение масштаба по каждой из осей, параллельному сдвигу границ снимка и повороту снимка). Рассмотрим более подробно эти преобразования. Преобразование первого порядка (аффинное преобразование), фактически это линейное преобразование. Оно может изменят: 1. положение точки по оси х и оси у
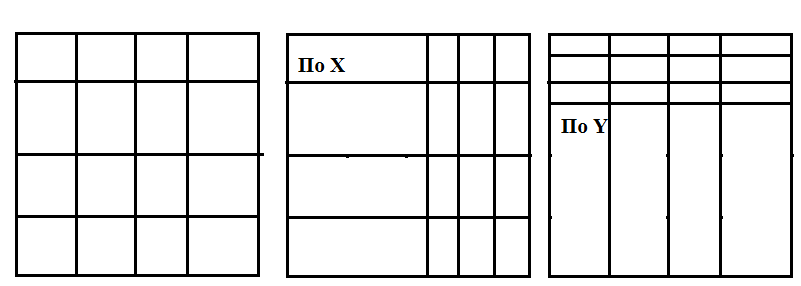
2. масштаб по х или по у,
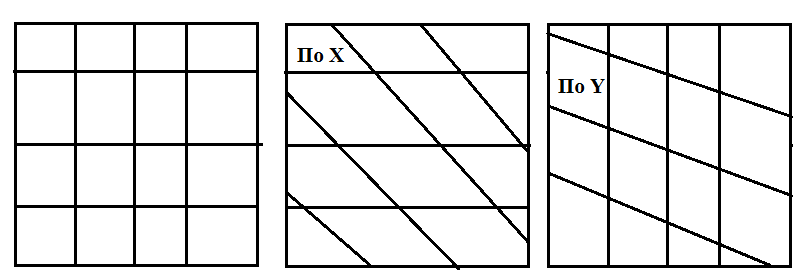
3. наклон по х и по у,
4. поворот, отражение.
Полином 1го порядка не может быть использован для перевода исходного изображения для перевода в прямоугольную систему координат, не может быть использован для перевода из одной прямоугольной системы координат в другую прямоугольную, т.е. используется всегда для небольших участков нашей поверхности. Преобразование 1го порядка может быть использовано для данных, которые уже спроецированы в прямоугольную плоскость. Фактически решение трансформации сводится к нахождению коэффициентов системы уравнений.
Xy координаты конечной системы координат, x’y’ координаты начальной системы координат. Все известны. Нужно найти a и b – 6 неизвестных. Для этого нам понадобятся 3 пары значений ху (3 точки).
Группируем по х и у и каждую группу и получаем для нахождения
Для получения коэффициентов каждая часть уравнений должна быть умножена на обратную матрицу.
Программное обеспечение должно работать с матрицами (ERDAS умеет). Коэффициенты подставляются в исходное уравнение и задача получения новых координат каждого пикселя решается для пикселя нового изображения.
Для решения теоретически необходимо знать координаты 3х точек. На практике – более 3х. Методом наименьших квадратов высчитывается среднеквадратичная ошибка
В результате можно вычислить суммарную среднеквадратичную ошибку, определить коэффициент и выделить ту точку, которая вносит наибольший вклад в эту ошибку. Как правило, всегда задается некий порог точности привязки, и если суммарная среднеквадратичная ошибка превышает пороговое значение, то точку исключают, и коэффициенты рассчитывают заново. И эту итерационную процедуру выполняют до тех пор, пока суммарная погрешность не станет меньше порогового значения или пока количество точек не станет равно 3.
Нелинейные преобразования.
Это полиномы 2го и большего порядков. Эти преобразования могут корректировать не линейные искажения.
Полиномы 2ой степени могут быть использованы для преобразования данных географической системы координат в прямоугольную, для преобразования данных больших областей (можем учитывать кривизну земли), для точной привязки искаженных по какой-либо причине данных. Матрица преобразований рассчитывается также по контрольным точкам, она состоит из коэффициентов. Размерность матриц зависит от порядка используемого преобразования. Коэффициенты матрицы преобразования рассчитывают таким образом, чтобы получить формулы полиномиального преобразования с как можно меньшей ошибкой перевода исходных данных в конечные, но получить эти коэффициенты получается не всегда.
Количество коэффициентов для преобразования.
Для двух – Каждая контрольная точка влияет на расчетный коэффициент, в случае если нет идеального соответствия каждой контрольной точки полиному, который представлен этими коэффициентами. Расстояние между кривой и точкой, т.е. между расчетной координатой и точкой на изображении – среднеквадратическая ошибка RMS. Для расчета матрицы преобразований по набору контрольных точек используется метод наименьших квадратов. Формула для вычисления полинома прядка Т.
t – порядок полинома
Расчет формул полиномов высоких порядков гораздо сложнее, чем расчет для полинома 1го порядка. Полиномы высоких порядков применяются только для изображений, у которых сильные и сложные искажения.
Полиномы 1,2,3,4 порядков. Минимальное количество точек для полиномов. 1 – 3 точки; 2 – 6 точек; 3 – 10 точек; 4 – 15 точек; 5 – 21 точка; 8 – 45 точек; 10 – 66 точек; 1. Способ резинового листа Rubbersheet - один из способов ортотрансформирования изображения построенного на основе центральной проекции. Способ используется при большом количестве равномерно расположенных плановых опорных точек. Поле точек объединяется способ в поле треугольников и используется триангуляция методом Делона. В данном методе используется аффинное преобразование для каждого треугольника. В данном случае для каждого треугольника параметры связи свои и они определяются использованием опорных точек. Процедура не контролируемая. Для точек, которые лежат на ребрах треугольника мы получаем координаты дважды, требуется геометрическое объединение фрагментов треугольников. 2. Spline - интерполяция 3. Интерполяция методом Крининга
|
||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 354; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.218.13.221 (0.006 с.) |



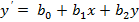
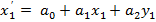
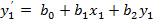

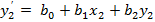
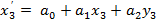
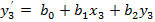

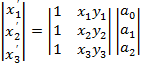
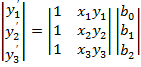

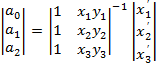
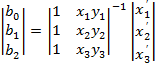
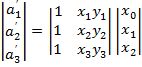
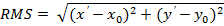
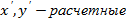
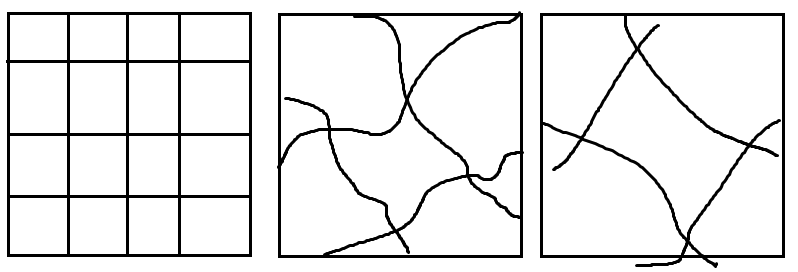

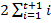 для одной координаты
для одной координаты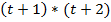
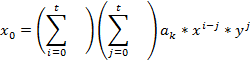
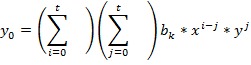

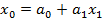 – смещение по одной оси
– смещение по одной оси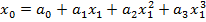
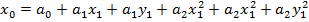 верхний индекс – степень полинома.
верхний индекс – степень полинома.



