Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные расчетные модели грунтовСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Требования к расчетным моделям Точность прогнозов в механике грунтов в большой степени определяется тем, с какой полнотой в уравнениях состояния отражаются особенности деформирования грунтов. При этом в практике проектирования для конкретных случаев используются расчетные модели грунта разной сложности. Для широкого круга задач строительства оказалось возможным выделить те, где основной является оценка несущей способности (прочности и устойчивости) грунтов. Напротив, в других задачах наиболее важным будет прогноз деформаций основания и сооружения. Наконец, в некоторых задачах необходимы и оценка несущей способности, и прогноз деформаций грунтов. Однако эти расчеты можно проводить раздельно, что позволило распространить на расчеты оснований общие принципы расчетов по предельным состояниям: · расчет по несущей способности (потеря устойчивости; хрупкое, вязкое или иного характера разрушения грунта; чрезмерные пластические деформации или деформации неустановившейся ползучести); · расчет по деформациям (достижение состояния, затрудняющего нормальную эксплуатацию сооружения или снижающего его долговечность вследствие недопустимых перемещений – осадок, разности осадок, кренов и т. п.). Существо расчетов по первой группе предельных состояний заключается в том, что расчетная нагрузка на основание не должна превышать силу предельного сопротивления грунтов основания. По второй группе предельных состояний совместная деформация сооружения и основания не должна превышать предельной для конструктивной схемы данного сооружения. Такой подход обусловил возможность использования наиболее простых расчетных моделей грунтов: для расчетов конечных напряжений и стабилизированных осадок – теории линейного деформирования грунта; для расчетов развития осадок во времени – теории фильтрационной консолидации грунта; для расчетов несущей способности, прочности, устойчивости и давления грунта на ограждения – теория предельного напряженного состояния грунта.
Модель теории линейного деформирования грунта Применимость этой модели к грунтам была впервые обоснована трудами Н. П. Пузыревского, К. Терцаги, Н. М. Герсеванова, В. А. Флорина, Н. А. Цытовича. Эта модель наиболее распространена в инженерной практике благодаря своей простоте и возможности использования хорошо разработанного математического аппарата теории упругости для описания напряженно-деформированного состояния грунтов. Теория линейного деформирования грунта базируется на предположении, что при однократном нагружении (или разгрузке) зависимость между напряжениями и деформациями в грунтах линейна. Кроме того, при нагружении рассматривается лишь общая деформация грунта без разделения ее на упругую и пластическую составляющие. Первое допущение обеспечивает возможность использования для расчетов напряжений в массиве грунта аппарата теории упругости, а второе – при известных напряжениях рассчитывать конечные деформации основания. Использование теории линейного деформирования грунта всегда требует установления предела ее применимости. Уравнения состояния модели теории линейного деформирования записываются в виде обобщенного закона Гука:
где Теорию линейного деформирования иногда называют теорией упругости грунтов. Формально это справедливо, так как она использует математический аппарат теории упругости. Однако нужно иметь в виду, что это сходство чисто формальное, так как теория линейного деформирования рассматривает общие деформации, не разделяя их на упругие и пластические. Кроме того, нагружение и разгрузка грунта в теории линейного деформирования происходят по разным законам и описываются различными по величине характеристиками деформируемости грунта.
Модель теории фильтрационной консолидации В наиболее простой постановке теория описывает деформирование во времени полностью водонасыщенного грунта (грунтовой массы). Принимается, что полное напряжение, возникающее в элементе грунта от приложенной нагрузки, разделяется на напряжения в скелете грунта (эффективные напряжения) и давление в поровой воде (поровое давление). В различных точках массива грунта под действием нагрузки возникают разные значения порового давления. Вследствие этого образуется разность напоров в поровой воде и происходит ее отжатие в менее нагруженные области массива. Одновременно под действием эффективных напряжений происходят перекомпоновка частиц и уплотнение грунта. Математическое описание этого процесса базируется на основной предпосылке о неразрывности среды, сформулированной академиком Н. Н. Павловским еще в 1922 г., т. е. считается, что уменьшение пористости грунта (его уплотнение) пропорционально расходу воды (оттоку воды из пор грунта). Следствием этого является важное положение о том, что скорость деформации грунта будет находиться в прямой зависимости от скорости фильтрации в нем поровой воды. Поэтому основной характеристикой грунта, определяющей время протекания процесса фильтрационной консолидации, является коэффициент фильтрации. В теории фильтрационной консолидации скелет грунта принимается линейно деформируемым. Следует отметить, что в инженерной практике используются и более сложные модели теории консолидации, учитывающие трехкомпонентный состав грунта, сжимаемость поровой воды, ползучесть скелета и другие процессы, возникающие в грунте при его деформациях. Такие модели описаны в трудах Н. М. Герсеванова, В. А. Флорина, М. А. Био, Ю. К. Зарецкого, З. Г. Тер-Мартиросяна и других ученых.
Модель теории предельного напряженного состояния грунта Данная модель относится только к предельному состоянию, т. е. к такому напряженному состоянию, когда в массиве грунта от действующих нагрузок сформировались значительные по размерам замкнутые области, в каждой точке которых устанавливается состояние предельного равновесия. Потому теорию предельного напряженного состояния часто называют теорией предельного равновесия грунта. Теория предельного равновесия грунта позволяет определить предельную нагрузку на основание (его предельная несущая способность), но при этом невозможно определить деформации грунта. Решения теории предельного равновесия используются также для общих расчетов устойчивости сооружений и оснований, откосов и склонов, определения давления грунта на ограждения. В основе современных решений теории предельного равновесия лежат фундаментальные работы В. В. Соколовского.
Теории нелинейного деформирования грунтов Теории нелинейного деформирования грунтов применяются для расчетов напряженно-деформированного состояния и оценки прочности оснований и грунтовых сооружений, когда связь между напряжениями и деформациями существенно нелинейна, поэтому они часто называются теориями пластичности грунтов. Значительное распространение в инженерной практике получила деформационная теория пластичности, основанная на теории малых упругопластических деформаций академика А. А. Ильюшина. В наиболее простом виде эта теория исходит из допущения, что объемная и сдвиговая деформации зависят только соответственно от среднего нормального напряжения и интенсивности касательных напряжений, т. е. Различные модификации теорий нелинейного деформирования грунтов представлены в работах С. С. Вялова, А. Л. Гольдина, Ю. К. Зарецкого, А. Л. Крыжановского, В. Г. Федоровского, В. И. Соломина, В. Г. Николаевского и др.
2. Физические свойства грунтов, классификация грунтов
2.1. Основные характеристики физических свойств грунтов, Физические свойства грунтов характеризуют их физическое состояние в условиях природного (ненарушенного) залегания. Исследование свойств грунтов предусматривает получение материала горных пород для определения показателей их физико-технических свойств – отбор проб. Количество отобранного грунта должно быть таким, чтобы состав и свойства пробы соответствовали составу и свойствам опробуемого слоя. Чем более неоднороден грунт, тем больше должна быть проба. Ее размер должен соответствовать технологическим требованиям лабораторных исследований, а общая масса материала должна быть достаточной для всего комплекса лабораторных работ. Отбираемые пробы могут быть с нарушенным или ненарушенным сложением (монолит). Чем меньше нарушается структура грунта в процессе его отбора и на всем пути следования до лаборатории, тем больше будет достоверность показателей. Пробы и монолиты отбирают из обнажений (мест выхода горных пород на земную поверхность) и из горных выработок (скважин, шурфов, штолен, траншей, расчисток и т. д.). Поскольку при нарушении структурных связей грунта его свойства изменяются, желательно изучать состояние грунта при ненарушенной структуре. Бурение скважин является основным видом разведочных работ при инженерно-геологических и гидрогеологических исследованиях. Буровая скважина – это цилиндрическая вертикальная (иногда наклонная или горизонтальная) горная выработка малого диаметра, выполняемая буровым инструментом. Начальную точку скважины называют устьем, а конечную забоем. Образцы горных пород, извлекаемые из скважины, называют керном, если они представляют собой монолиты цилиндрической формы, или шламом, если порода раздроблена. Диаметр скважин, используемых при инженерно-геологических изысканиях, обычно находится в пределах от 34 до 273 мм (для гидрогеологических целей – больше). Глубина скважин определяется задачами исследований и для инженерно-строительной целей редко превышает 30 м, а при поиске вод для водоснабжения может быть более 800 м. К преимуществам бурения относят высокую скорость проходки, возможность достижения больших глубин, механизацию операций, мобильность установок. Недостатками метода являются невозможность осмотра стенок скважины, небольшой размер образцов, необходимость промывки скважины при бурении. По окончании полевых работ из скважин извлекают инструмент и обсадные трубы, выработки тщательно цементируют, грунт утрамбовывают, а поверхность земли выравнивают. Проходка шурфов осуществляется путем разрушения пород в забое горной выработки и извлечения их на поверхность Земли. При небольших объемах работ разрушение Недостатком шурфов является высокая стоимость и трудоемкость работ, особенно в скальных горных породах. В малоустойчивых породах стенки шурфов приходиться крепить. При проходке водонасыщенных пород организуют водоотлив. По окончании полевых работ шурфы ликвидируют аналогично скважинам (засыпка, трамбование). Из открытых горных выработок и обнажений монолиты вырезают в форме куба или параллелепипеда со сторонами не менее 100 мм и не более 250 мм с помощью ножа и лопаты (см. рис. 2.1). Шурфы позволяют детально изучить геолого-литологический разрез участка, отобрать любые по размеру образцы грунтов и проводить опытные полевые работы. Консервация образцов. С целью сохранения естественной влажности, отобранные монолиты и пробы подлежат немедленной консервации способом парафинирования. Монолит или керн обматывают двумя слоями марли, крупнозернистые и пористые грунты заворачивают в полиэтилен. Транспортировка проб. Нарушенные образцы отправляют в лабораторию в жестких обоймах (металлических или пластмассовых банках). Открытые грани образцов закрывают герметичными крышками, горловину банки парафинируют. Если не требуется сохранить влажность, образцы помещают в мешочки или в ящики, снабдив двумя этикетками. Хранение проб. Образцы хранят при температуре не менее 2 ºС и не более 20 ºС при относительной влажности не более 80 %. Монолиты грунтов текучепластичной и
Рис. 2.1. Отбор монолитов грунта: Подготовка проб к исследованию. Для непосредственной подготовки пробы к анализу ее сокращают методом квартования. Для этого из общей пробы воздушно-сухого грунта отбирают не менее 100 г мелко- и среднезернистых песков, не менее 400 г крупнозернистых песков и гравия, не менее 4 кг щебня и галечника. Грунт тщательно перемешивают и распределяют по ровной поверхности слоем около 0,5 см. Затем двумя взаимно перпендикулярными линиями разделяют на 4 равные части – квадранты. Два противоположных по диагонали квадранта оставляют в качестве сокращенной пробы, два других удаляют. Эти действия продолжают до тех пор, пока не остается необходимый объем грунта. Показатели некоторых физических свойств грунтов могут определяться непосредственно в полевых условиях без отбора образцов с применением косвенных способов исследования, например, зондирования. Также непосредственно в полевых условиях (визуально) можно предварительно определить вид грунта (табл. 2.1).
Таблица 2.1 Определение вида грунта в полевых условиях (визуально)
Наиболее приемлемыми для последующего использования в расчетах следует полагать показатели (характеристики) определений, произведенных для данных конкретных разновидностей грунтов. Однако за неимением результатов таких определений можно воспользоваться результатами испытаний аналогичных грунтов, но достаточно близких к тем, которые залегают в основании сооружения. Можно иногда воспользоваться результатами, полученными в данной местности и в другое время ранее или, наконец, результатами других статистических обобщений. Все это зависит от важности, назначения и категории объекта. Вследствие неоднородности любого рассматриваемого слоя грунта и ошибок при измерениях во время экспериментального определения характеристик грунта эти величины находят многократно, и полученные результаты обрабатывают методами математической статистики. Минимально в математической статистике принято считать достаточным 6 определений. Однако чем большее количество результатов определений введено в формулу для статистического нахождения среднего значения, тем «точнее» оказывается результат. Нормативными считаются средние значения показателей или характеристик, определяемые как среднеарифметические. Если характеристику обозначить через X, При переходе к расчетному значению учитывается, что среднее значение вследствие неоднородности грунта и ограниченного числа определений может содержать ошибку, которая должна быть исключена. Ошибки могут быть прямыми, связанными с применением неправильной методики определения, или плохой аппаратурой – это ошибки систематические. Для грунтов характерно свойство флуктуации, то есть случайных отклонений величин характеристик, которые характеризуют систему из большого числа элементов, от их среднего значения. Ошибки, точнее отскоки, могут быть большими. Такие ошибки называются грубыми, и эти величины исключаются из дальнейшего рассмотрения. Ошибки ei величин, включаемых в рассматриваемую совокупность, из которой исключены большие случайные отскоки, устанавливаются как разности При испытаниях следует выполнять требования соответствующих государственных стандартов, если они имеются, или различных ведомственных нормативных документов. Для испытаний используются стационарные, либо полевые лаборатории. Предпочтительными являются прямые методы испытаний, но в ряде случаев используются результаты косвенных методов исследования.
2.2. Основные, производные и классификационные Физические характеристики грунтов позволяют количественно оценить их свойства и не зависят от применяемых методов расчета грунтовых сред. Ряд физических характеристик грунтов может быть получен, исходя из представления грунта как многокомпонентной среды, в общем случае состоящей из твердых частиц, жидкости (воды) и газа (рис. 2.2). Различают физические, прочностные и деформационные характеристики грунта. Физические характеристики подразделяются на основные, производные и классификационные. Основными являются характеристики, определяемые из опыта. Остальные физические характеристики являются расчетными. Введем следующие условные обозначения физических величин, показанных на рис. 2.2; ρw, γw – плотность и удельный вес воды; g – ускорение свободного падения.
Рис. 2.2. Модель грунта: V – объем образца грунта; Vs – объем минеральных частиц грунта в объеме V; Vn – объем пор Данные о свойствах грунтов для наглядности представим в табличной форме (табл. 2.2, 2.3, 2.4). В формулах плотность воды pw обычно принимают равной 1 г/см3 (или 1 т/м3), удельный вес γw равным 10 кН/м3. Строго говоря, это не соответствует действительности, так как плотность прочносвязанной воды существенно больше единицы. Однако методика определения pw с учетом плотности связанной воды, большей по сравнению со свободной, пока еще не разработана. Кроме того, при малом количестве прочносвязанной воды в грунте погрешность при расчете небольшая.
Таблица 2.2
Основные физические характеристики грунта
Таблица 2.3
Производные физические характеристики грунта
Таблица 2.4 Классификационные физические характеристики грунта
Приведенные в таблицах формулы для вычисления производных и классификационных физических характеристик грунта получены в результате преобразования выражений, являющихся определениями этих характеристик:
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 2627; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.148.108.174 (0.013 с.) |

 ;
;  ;
; ;
; 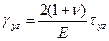 ;
; ;
;  ,
, – модуль общей линейной деформации;
– модуль общей линейной деформации;  – коэффициент поперечного линейного расширения (коэффициент Пуассона).
– коэффициент поперечного линейного расширения (коэффициент Пуассона). ;
;  . Однако деформационная теория пластичности не учитывает некоторые процессы, происходящие в грунте. Более точные решения можно получить с помощью теории пластического течения. Однако это приводит к усложнению экспериментов для определения параметров уравнения состояния и расчетного аппарата анализа. Теорию пластического течения применяют при решении сложных задач гидротехнического строительства.
. Однако деформационная теория пластичности не учитывает некоторые процессы, происходящие в грунте. Более точные решения можно получить с помощью теории пластического течения. Однако это приводит к усложнению экспериментов для определения параметров уравнения состояния и расчетного аппарата анализа. Теорию пластического течения применяют при решении сложных задач гидротехнического строительства.


 . Чтобы использовать в расчете характеристику, следует найти ее расчетное значение
. Чтобы использовать в расчете характеристику, следует найти ее расчетное значение  , где γn – безразмерный коэффициент надежности. Для физических характеристик грунта коэффициент надежности часто принимается γn =1.
, где γn – безразмерный коэффициент надежности. Для физических характеристик грунта коэффициент надежности часто принимается γn =1. . Относительные ошибки вычисляются по формуле
. Относительные ошибки вычисляются по формуле 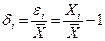 . Средние значения ошибок вычисляются либо как
. Средние значения ошибок вычисляются либо как  , либо как среднеквадратичные отклонения, равные
, либо как среднеквадратичные отклонения, равные  .
.


 ,
e max – коэффициент пористости грунта в max рыхлом его состоянии; e min – коэффициент пористости грунтов в min рыхлом его состоянии
,
e max – коэффициент пористости грунта в max рыхлом его состоянии; e min – коэффициент пористости грунтов в min рыхлом его состоянии

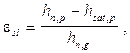 где
где  и
и  – высота образца соответственно природной влажности и после его полного водонасыщения (w = w (sat)) при давлении p, равном вертикальному напряжению на рассмат- риваемой глубине от внешней нагрузки и собственного веса грунта
– высота образца соответственно природной влажности и после его полного водонасыщения (w = w (sat)) при давлении p, равном вертикальному напряжению на рассмат- риваемой глубине от внешней нагрузки и собственного веса грунта

 – высота того же образца природной влажности при
– высота того же образца природной влажности при