
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Доказательство применимости теории упругости к грунтам (постулаты теории упругости).
1. Деформации пропорциональны напряжениям
Рис. 4.2. Зависимость между осадкой и нагрузкой на штамп
2. Теория упругости рассматривает тела упругие. В грунтах наблюдаются большие остаточные деформации Sост. Но для строителей существенно одноразовое загружение основания, т. е. здесь условие упругости применимо
3. Теория упругости рассматривает тела сплошные. Вследствие зернистости грунта установить истинное напряжение, возникающее в какой-либо точке его массива, с использованием теории упругости невозможно. Приходится ограничиваться определением средней интенсивности напряжения σ ср в требуемой точке основания, принимая условно, что грунт является сплошным телом. В точках контактов частиц напряжения будут во много раз больше средних значений. В этом случае можно говорить о «сплошности» грунтов. 4. Теория упругости рассматривает тела изотропные. Иногда грунты обладают анизотропией, обусловленной как характером их образования, так и предшествующим напряженным состоянием. Тем не менее при решении инженерных задач с некоторым приближением обычно принимают, что грунты изотропны. Это во многих случаях близко к действительности (для песков, неслоистых глин и суглинков и т. п.). При необходимости можно учесть анизотропность грунтов, но это приводит к усложнению расчетов. (Будем считать, с известными допущениями, что грунт – изотропное тело). Таким образом, при определении напряжений в массиве принимают, что грунт является сплошным линейно-деформируемым телом, испытывающим одноразовое загружение. При этих условиях для определения осредненных напряжений в точке массива грунта используют решения теории упругости.
4.3. Напряжения, возникающие от действия внешних нагрузок. Действие сосредоточенных сил, распределенной нагрузки. Действие равномерно распределенного давления, метод угловых точек
Проблемы распределения напряжений в грунтовом массиве рассматриваются в фазе его уплотнения. Фаза уплотнения является стадией его напряженно-деформированного состояния, представляющей наибольший интерес для практики, так как при реальном проектировании напряжения в грунтовом массиве ограничиваются величиной, незначительно превышающей начальное критическое давление. Важнейшим следствием принципа линейной деформируемости, применимость которого находится в диапазоне напряжений, соответствующих фазе уплотнения, является правомерность использования для анализа напряженно-деформированного состояния грунтового массива аппарата теории упругости. При этом в указанном анализе модуль упругости должен быть заменен на модуль деформации, комплексно учитывающий развитие как упругих, так и пластических деформаций грунта. В общем случае задача о распределении напряжений в грунтовом массиве при заданных краевых условиях может быть сведена к решению дифференциальных уравнений равновесия, дополненных уравнениями совместности деформаций и физическими уравнениями в форме закона Гука. Такие задачи, как правило, решаются численными методами, так как получение для них замкнутых аналитических решений является весьма проблематичным (подынтегральные функции не являются, как правило, полными дифференциалами). По этой причине представляют особый практический интерес аналитические решения, полученные с использованием только уравнений равновесия на основании упрощающих гипотез. К таким решениям относится широко известная в механике грунтов задача Буссинеска о распределении напряжений в упругом полупространстве от действия вертикальной сосредоточенной силы на граничной плоскости. Представляют практический интерес не столько решения указанной задачи, сколько ее приложения. Используя принцип суперпозиций, решены задачи о распределении напряжений в грунтовом массиве при произвольной нагрузке на граничной плоскости полупространства, основанные на интегрировании решения Буссинеска.
Определение напряжений Решение задачи Буссинеска. Основано на следующих гипотезах (впоследствии подтвержденных точными решениями): а) нормальные напряжения на площадках, касательных к сферической поверхности с центром в точке приложения силы, являются главными напряжениями. По этой причине касательные напряжения на указанных площадках отсутствуют; б) нормальные напряжения, лежащие в вертикальной плоскости, на площадках, нормальных к сферической поверхности с центром в точке приложения силы, равны нулю; в) нормальные напряжения на площадках, касательных к сферической поверхности с центром в точке приложения силы, прямо пропорциональны косинусу угла видимости и обратно пропорциональны квадрату радиуса сферы. Под углом видимости понимается угол между радиусом сферы, проведенным в центр площадки, и центральной вертикальной осью сферы. Постулированные гипотезы позволяют получить замкнутые аналитические решения о распределении напряжений в полупространстве от действия вертикальной силы на его границе, основанные исключительно на уравнениях равновесия. Решение задачи поясняется графическими построениями на рис. 4.5, на котором представлены вертикальный разрез полупространства и его сечения горизонтальными плоскостями. Начало прямоугольной декартовой системы координат разместим в точке приложения вертикальной силы Р на границе полупространства. Ось z направим по вертикали вниз, ось x – по горизонтали вправо, а ось y – перпендикулярно плоскости чертежа. Относительно начала осей координат построена полусфера радиусом R, пересечение которой с вертикальной плоскостью, проходящей через центральную ось, образует полуокружность такого же радиуса. В сечении полусферы горизонтальной плоскостью на глубине z образуется окружность радиусом r. Угол видимости радиуса r на вертикальном разрезе обозначим β.
Рис. 4.5. Графическое построение к решению задачи Буссинеска
Условие равновесия:
В соответствии с гипотезой в), σR = A cosβ/ R 2. Кроме этого, r = R ⋅ sinβ. Подставляя в уравнение (3.1) выражения для σR и r и выполняя преобразования, получим:
Выполняем замену переменных в уравнении (4.2): u = cosβ, du = − sinβ ⋅ d β. Продолжая преобразования, получим выражение для неопределенного коэффициента А:
Выразим cosβ через ординату z: cosβ = z / R. С учетом этого, формула для определения напряжения σR будет иметь вид
Практический интерес представляют напряжения на горизонтальной площадке, наклоненной к площадке, на которой действуют напряжения σR, под углом β. В соответствии с гипотезой б) главный вектор напряжений на горизонтальной площадке σ′R совпадает по направлению с вектором напряжения σR, а его модуль равен σ′R = σR ⋅ cosβ. Проекции главного вектора напряжений σ′R на координатные оси являются компонентами тензора напряжений на горизонтальной площадке. Поскольку главный вектор напряжений σ′R совпадает по направлению с радиусом вектором R, направляющие косинусы вектора напряжений определяются формулами:
С учетом полученных выше зависимостей, компоненты тензора напряжений на
Формулу для σz обычно табулируют. Для этого выполняют следующие преобразования:
В дальнейшем для практических расчетов расчетную схему задачи приводят к более простому виду (рис. 4.6). Вертикальные напряжения в расчетной точке М определяют по формуле
Z – глубина точки; r – расстояние от точки до линии действия силы; М – рассматриваемая точка; N – сосредоточенная вертикальная сила.
|
|||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 1209; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.128.199.162 (0.014 с.) |


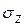 в массиве грунта при действии единичной вертикальной силы N, приложенной к границе грунтового основания.
в массиве грунта при действии единичной вертикальной силы N, приложенной к границе грунтового основания.
 (4.1)
(4.1) (4.2)
(4.2)

 ; (4.3)
; (4.3)


 . (4.4)
. (4.4)
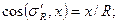
 . (4.5)
. (4.5)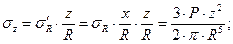
 ; (4.6)
; (4.6) .
.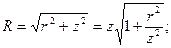 (4.7)
(4.7) , (4.8)
, (4.8)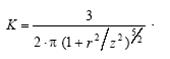

 .
.


