
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение напряжений в массиве грунта от действия нескольких вертикальных сосредоточенных сил, приложенных к границе грунтового основания (принцип Сен-Венана – принцип независимости действия сил).Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Рис. 4.7. Схема к определению напряжений в массиве грунта от действия нескольких вертикальных сосредоточенных сил
Если к поверхности изотропного линейно-деформируемого полупространства приложено несколько сил (N 1, N 2,..., Nn), то при прямой пропорциональности между напряжениями и деформациями можно использовать принцип суперпозиции и найти значение σz в любой точке М простым суммированием:
Коэффициент К, зависящий от безразмерного параметра r/z, определяется так же как и в предыдущем случае. Определение напряжений σz в массиве грунта при действии любой распределенной нагрузки, приложенной к границе грунтового основания (метод элементарного суммирования). Пусть к поверхности изотропного линейно-деформируемого полупространства в пределах площади загружения приложено распределенное давление. Загруженную площадь можно разбить на небольшие прямоугольники и более сложные фигуры по ее контуру.
Рис. 4.8. Схема к определению напряжений в массиве грунтапри действии любой распределенной нагрузки
Определив величину szi от нагрузки каждой из небольших фигур, на которые разбита площадь загружения, и произведя суммирование этих напряжений, определим напряжение szi от действия распределенной нагрузки (аналогично формуле 4.9):
Этот метод также иногда называют методом элементарных квадратов. Коэффициент К, зависящий от безразмерного параметра r/z, определяется так же как и в предыдущих случаях. Точность расчета увеличивается с уменьшением размеров отдельных элементов, однако при большом числе элементов значительно увеличивается трудоемкость задачи. Определение напряжений σz при действии местного равномерно распределенного давления (метод угловых точек). Если закон распределения давления по поверхности изотропного линейно-деформируемого полупространства известен, то элементарное суммирование можно заменить интегрированием.
где
Рис. 4.9. Расчетные схемы к определению напряжений
При нахождении Напряжение под угловыми точками определяют по формуле
Для определения вертикального напряжения
Рис. 4.10. Расчетные схемы к определению напряжений
Таблица 4.2 Определение коэффициента α
Окончание табл. 4.2
Тогда напряжение
где Когда проекция точки М' на горизонтальную поверхность полупространства (точка М)располагается вне пределов площади загружения (рис. 4.6, б), точку М аналогично можно представить как угловую точку фиктивных площадей загружения I, II, III, IV. При этом в пределах площадей II и IV фиктивная нагрузка прикладывается в обратном направлении. Напряжение определяется по выражению
sz =
Обобщая формулы, можно дать следующее определение методу угловых точек: напряжение в произвольной точке от нагрузки, распределенной по прямоугольной площади, равно алгебраической сумме напряжений в угловых точках прямоугольников, для которых рассматриваемая точка является угловой, при этом алгебраическая сумма площадей этих прямоугольников с учетом знаков в формуле суммирования напряжений должна совпадать с фактической площадью нагрузки. Так, пользуясь методом угловых точек, можно найти напряжение sz в любой точке полупространства, к поверхности которого приложена равномерно распределенная нагрузка в пределах прямоугольной площади. 4.4. Напряжения, возникающие от действия собственного веса грунта Фактическое напряженное состояние грунтов основания при современных методах изысканий точно определить не представляется возможным. В большинстве случаев ограничиваются нахождением вертикального напряжения от действия веса вышележащих грунтов. Вертикальные напряжения от собственного веса грунта называют бытовыми давлениями, а график их изменения по глубине – эпюрой бытовых давлений. Напряжения от собственного веса грунта определяются на основании следующих упрощающих гипотез: 1) напряженным состоянием грунта при действии его собственного веса является осесимметричное компрессионное сжатие; 2) вертикальные напряжения в грунте определяются суммированием напряжений от веса элементарных слоев грунта; 3) грунт, находящийся ниже уровня грунтовых вод, испытывает взвешивающее действие воды; Определяем напряжение от собственного веса грунта (природного или бытового) по формуле
где n – число слоев грунта в пределах глубины z; gi – удельный вес грунта i -го слоя, кН/м3; Удельный вес водопроницаемых грунтов, залегающих ниже уровня грунтовых вод, принимается с учетом взвешивающего действия воды согласно выражению
gsb= (gs – gw) / (1+ e),
где gw – удельный вес воды, gw = 10 кН/м3; gs – удельный вес частиц грунта; Формула используется для вычисления бытовых давлений на границах геологических слоев, на линии уровня грунтовых вод и на границе водоупора. В остальных сечениях бытовые давления могут быть определены по линейной интерполяции. На рис. 4.11 представлены характерные эпюры бытовых давлений в грунтовом массиве. На границах геологических слоев угол наклона эпюры, как правило, изменяется в связи с изменением величины удельного веса грунта. На линии уровня грунтовых вод (WL) имеет место самый заметный перегиб эпюры, вызванный уменьшением удельного веса грунта во взвешенном состоянии. На границе водоупора эпюра имеет скачок на величину гидростатического давления от веса столба воды над водоупором. Деформации от действия веса природного грунта считаются давно стабилизировавшимися. Исключение составляют случаи действия свежеотсыпанной насыпи или понижения уровня подземных вод. При большой мощности толщи насыщенных водой сильносжимаемых грунтов, обладающих ползучестью, иногда приходится считаться с незавершенной фильтрационной консолидацией и консолидацией ползучести.
Рис. 4.11. Характерные эпюры распределения бытовых напряжений в массиве грунта:
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 2133; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.38.120 (0.007 с.) |


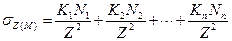 , (4.9)
, (4.9) .
. .
.
 ,
, .
. =
=  – при разворачивании этого интеграла получается очень громоздкая формула, поэтому при равномерно распределенном давлении после интегрирования по прямоугольной площади загружения значения для точек, расположенных под центром прямоугольной площади загружения (рис. 4.9, а), получим:
– при разворачивании этого интеграла получается очень громоздкая формула, поэтому при равномерно распределенном давлении после интегрирования по прямоугольной площади загружения значения для точек, расположенных под центром прямоугольной площади загружения (рис. 4.9, а), получим: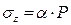 , (4.10)
, (4.10) = f
= f  – принимается по таблице 4.2; Р – равномерно распределенное давление.
– принимается по таблице 4.2; Р – равномерно распределенное давление.
 при действии местного равномерно распределенного давления: а – для точек, расположенных под центром прямоугольной площади загружения; б – под угловыми точками прямоугольной площади загружения
при действии местного равномерно распределенного давления: а – для точек, расположенных под центром прямоугольной площади загружения; б – под угловыми точками прямоугольной площади загружения под угловыми точками прямоугольной площади загружения (например, под точкой М) (рис. 4.9, б),значения
под угловыми точками прямоугольной площади загружения (например, под точкой М) (рис. 4.9, б),значения  (а не 2∙ Z, т. к. в 1=2 в), также можно принимать по таблице 4.2.
(а не 2∙ Z, т. к. в 1=2 в), также можно принимать по таблице 4.2. =
=  .
. в любой точке полупространства можно воспользоваться выражением
в любой точке полупространства можно воспользоваться выражением  =
=  . Действительно, если проекция рассматриваемой точки М ' на горизонтальную поверхность полупространства (точка М)располагается в пределах площади загружения (рис. 4.10, а), то эту площадь можно разбить на четыре прямоугольника (I – Meaf, II – Mfbg, III – Mgch, IV – Mhde)так, чтобы точка М была угловой точкой каждого из них.
. Действительно, если проекция рассматриваемой точки М ' на горизонтальную поверхность полупространства (точка М)располагается в пределах площади загружения (рис. 4.10, а), то эту площадь можно разбить на четыре прямоугольника (I – Meaf, II – Mfbg, III – Mgch, IV – Mhde)так, чтобы точка М была угловой точкой каждого из них.
 найдем суммированием напряжений под угловыми точками четырех площадей загружения:
найдем суммированием напряжений под угловыми точками четырех площадей загружения: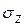 =
=  ,
, – коэффициенты, принимаемые по таблице в зависимости от отношения сторон площадей загружения I, II, III, IV и отношения Z (глубины расположения точки М')к ширине каждой из этих площадей.
– коэффициенты, принимаемые по таблице в зависимости от отношения сторон площадей загружения I, II, III, IV и отношения Z (глубины расположения точки М')к ширине каждой из этих площадей. .
. ,
,  ,
,



