
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Критерії оптимальності приймача.Содержание книги
Поиск на нашем сайте В процесі виявлення сигналу можуть бути помилки двох видів: 1) рішення про наявність сигналу, коли насправді є тільки шум (хибна тривога) Рхт; 2) рішення про відсутність сигналу, коли сигнал дійсно є (пропуск сигналу) Рпр; В залежності від ймовірності помилок введені критерії: - Згідно з критерієм ідеального спостерігача приймач є оптимальним, якщо він забезпечує мінімальну ймовірність помилки будь якого виду. Згідно критерієм Неймана-Пірсона приймач є оптимальним, якщо він забезпечує максимальну ймовірність правильного виявлення, мінімальну ймовірність пропуску сигналу при заданій ймовірності помилкової тривоги. Критерій Неймана-Пірсона найбільше застосовується в радіолокації. Відомі інші критерії оптимальності приймача (критерій Байєса, мінімаксний критерій, критерій втрати інформації). В загальному випадку різним критеріям оптимальності відповідають різні структури і властивості оптимального приймача.
Теорема Байеса — одна из основных теорем элементарной теории вероятностей, которая определяет вероятность наступления события в условиях, когда на основе наблюдений известна лишь некоторая частичная информация о событиях; по формуле Байеса можно пересчитывать вероятность, беря в учет как ранее известную информацию, так и данные новых наблюдений. Формула Байеса позволяет вычислить условную плотность вероятности х на входе, если задан y. Формула Баєса: w(x)- априорная плотность вероятности x вектора сигнала(до ввода), w(y)- безусловная плотность вероятности вектора y; w(y|x)- условная плотность вероятности y если x задан Для определения апостериорной вероятности P(x|y) или плотности вероятности w(x|y) необходимо знать плотность вероятности w(y|x), которая при заданном y будет зависить только от x, то есть w(y|x)=L(x) – функция правдоподобия. В зависимости от того являються ли х дискр. или непрер. величиной функция правдоподобн. может принять конечное или бесконечное множество значений. Значение функции правдоподобия w(y|x)=L(x) это условная плотность вероятности выборки у при наличии полезного сигнала х, а L(x0)=w(x|x0) условная плотность вероятности выборки у при отсутствии х, в случае когда есть только шум. Потери, которые возникают при ошибочном решении, что был принят сигнал
т.е. определяется суммой вероятностей ошибок с учётом потерь Если
где Качество канала передачи сообщений тем выше, чем меньше средний риск R в (32). Критерий среднего риска является одним из наиболее общих. Это Байесовский критерий, поскольку он основан на априорно известных вероятности передачи отдельных сигналов и условной вероятности на приемной стороне, что позволяет воспользоваться формулой Байеса в (32).критерий Неймана-Пирсона можно интерпретировать как частный случай Байесовского критерия. Для случая различения сигналов
где
Левая часть неравенства (46) носит название отношения правдоподобия. Правая часть в случае неизвестных вероятностей отсутствия и наличия сигнала также неизвестна, поэтому принимают, что отношение правдоподобия должно быть выше заданного порогового значения P. Таким образом, пространство X реализаций x преобразуется в значения P на числовой оси, так что условные вероятности принять сигнал при условии его наличия или отсутствия выражаются в форме
Поэтому при установленной границе
Структура оптимального приемника Неймана-Пирсона строится так, чтобы выполнялось условие
|
||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 247; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.165.204 (0.006 с.) |

 , где
, где , когда на самом деле передавался
, когда на самом деле передавался  обозначим
обозначим  . Естественно принять
. Естественно принять  . Условный риск при передаче есть
. Условный риск при передаче есть  (31)
(31) – априорная вероятность передачи сигналов
– априорная вероятность передачи сигналов 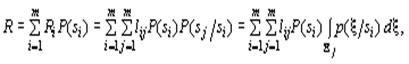 (32)
(32)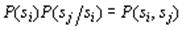 – безусловная вероятность.
– безусловная вероятность. используем соотношение
используем соотношение (42)
(42) – апостериорная вероятность того, что передавался сигнал
– апостериорная вероятность того, что передавался сигнал  (43)Условие максимума апостериорной вероятности есть
(43)Условие максимума апостериорной вероятности есть  В случае обнаружения сигнала
В случае обнаружения сигнала  должно выполняться условие
должно выполняться условие (44) или
(44) или  (45)
(45)  (46)
(46) (47)
(47)  (48)
(48)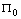 принятия решений
принятия решений (49)
(49) 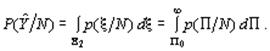 (50)
(50) .
.


