
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Оптимальний прийом інформації в ЕС. Критерій оптимальності.Содержание книги
Поиск на нашем сайте
Рассматриваются классические информационные меры -шенноновская, фишеровская информация, дивергенция Кульбака и их взаимосвязь. Приводится информационная трактовка классических правил выбора статистических решений. Рассматривается оптимальное байесовское правило, распознавания сигналов с позиций использования максимально возможной информацию! о распознаваемых объектах I. Взаимосвязь основных информационных мер При распознавании М классов объектов, представленных случайными сигналами, шенноновская информация, которая содержится в наблюдении y относительногипотезы Hj имеет вид
где Соответственно средняя шенноновская информация относительно гипотезы Hj, по всему ансамблю реализаций определяется соотношением
Согласно (2) разность средних шенноновских информаций, содержащихся во всём ансамбле реализаций сигналов относительно гипотез Hiи Hj, равняется
Эту разность информаций называют расхождением (дивергенцией) Кульбака между гипотезами Hiи Hjили между мерами В задаче оценки непрерывного параметра индивидуальная шенноновская информация, которая содержится в сообщениях относительно значения параметра
А средняя информация – соответственно вид
Разность средних шенноновских информаций, которые содержатся в ансамбле сигналов относительно значений параметра
где
В частнои скалярного параметра выражение (4) принимает вид
где информация Шифера.
Таким образом, классические информационные меры 1 взаимосвязаны: дивергенция Кульбака - это разность средних шенноновеких информация, содержащихся в ансамбле реализаций сигналов относительно двух выдвинутых гипотез; фишеровская] информация - это взятая со знаком минус производная средней щенноновской информации, которая содержится в ансамбле реализаций относительно конкретного значения непрерывного параметра сигнала. Оптимальный прием сигналов с позиций информационного критерия оптимальности В теории статистических решений обычно забывают про задачу сохранения информации и ставят задачу - построения решающих правил, оптимальных по иным критериям – минимума среднего риска, минимума средней вероятности ошибки и др. Более естественно использовать информационные критерии, выдвигающие требования сохранения информации о распознаваемых объектах. Иногда эти подхода приводят к одинаковым решающим правилам. Рассмотрим такой информационный критерий: выбрать среди M гипотез такую, относительно которой в принятой реализации содержится максимум взаимной шенноковской информации:
Для конечномерных наблюдений решающее правило (5) может быть приведено к виду
который совпадает с алгоритмом, оптимальным по критерию! максимума правдоподобия, мало понятного с позиций передачи
информации от распознаваемых объектов.(Здесь функция правдоподобия). Алгоритмы распознавания, оптимальные по классическим критериям оптимальности, могут быть выражены через информационные характеристики сигналов. Так алгоритм, оптимальный по минимуму средней вероятности ошибки, принимает вид:
Здесь Pi -вероятности предъявляемых сигналов, Решающие правила (6) (7) основаны на информативности наблюдений относительно каждой гипотезы, а также учитывают вероятности гипотез и "плату" за различные решения. 3.Качество оптимального приема сигналов с позиций информативности наблюдений Классический подход к построению правил распознавания сигналов в рамках байесовской теории статистических решений, требующий минимизации среднего риска, в явном виде не учитывает мание сохранения информации в наблюдениях. В общем случае переход от принятых реализаций сигналов к некоторым статистикам приводит к ухудшению качества распознавания. С позиций шенноновской информации рассмотрено понятие достаточной статистики относительно задачи распознавания случайных сигналов. Статистика рассмотрена как отображение, задающее разбиение пространства реализаций сигналов на непересекающиеся множества. Показано, что статистика относительно задачи распознавания сигналов будет достаточной горда и только тогда, когда при переходе к ней не изменяется средняя шенноновская информация относительно выдвигаемых
Сформулирована фундаментальная теорема относительно байесовского правила распознавания сигналов. Согласно этой теореме, байесовское правило, построенное в пространстве наблюдений, минимизирует средний риск по сравнению с многими другими решающими правилами. Однако величина этого минимума различна для разных статистик. Она наименьшая, когда правило набора решений строится непосредственно в пространстве реализаций принятого сигнала или в пространстве наблюдений, которые являются достаточными статистиками. Использование ими статистик и построение в них решающего правила не дает минимальной величины минимума среднего риска.
|
||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 233; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.134.247 (0.008 с.) |

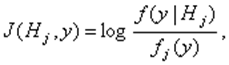 (1)
(1)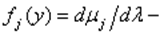 произвольная Радона-Никодима меры
произвольная Радона-Никодима меры 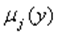 по отношению к мере
по отношению к мере 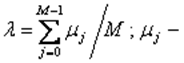 мера, заданная на множестве реализаций j-го сигнала, определяющего его.
мера, заданная на множестве реализаций j-го сигнала, определяющего его.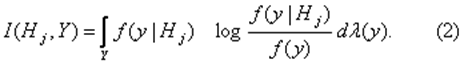
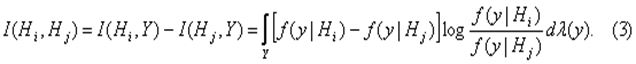
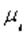 и
и 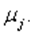
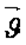 , имеет вид
, имеет вид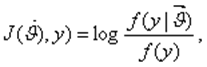
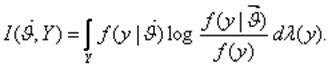
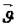 и
и 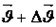 равна
равна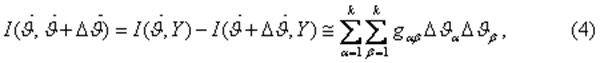
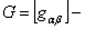 информационная матрица Фишера;
информационная матрица Фишера;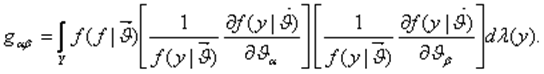
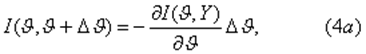
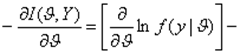
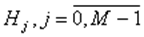
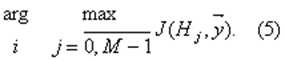
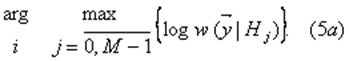
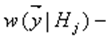
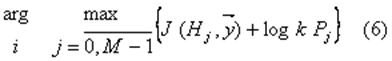
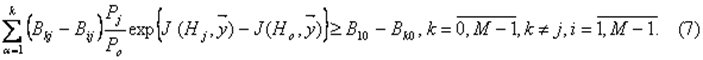 алгоритм, оптимальный по критерию минимума среднего риска - вид
алгоритм, оптимальный по критерию минимума среднего риска - вид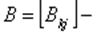 матрица потерь.
матрица потерь.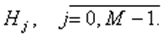 Гипотез
Гипотез


