
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Fundamental system of solutionsСодержание книги
Поиск на нашем сайте
Definition. System of n linearly independent solutions of system Theorem. The system
Concept of the fundamental matrix. Ostrogradsky-Liouville formula. We consider the system
of n arbitrary vector solutions of the vector equation Y(t) = and the Wronskian. If the system of vectors 40 Integration of linear inhomogeneous equation with quasipolinomial right side. The particular solution y * (x) can be solved by trial, if the right side of the equation - quasipolynomial - function of the form f (x) = exp(α x)(Mm (x)cos(β x) + Nn (x)sin(β x)). Here Mm (x) - a polynomial of degree m, Nn (x) - a polynomial of degree n, α and β - are real numbers. Calculation method of selection of a particular solution of the inhomogeneous linear equations with quasipolynomial in the right side is the following. Carefully look at the right side of the equation and write down the number of α ± βi. Then the characteristic equation of the homogeneous equation and find its roots. There are two cases: the roots of the characteristic polynomial is no root, equal to the number of α ± βi (nonresonantce case), and among the roots of the characteristic polynomial is r roots equal to the number of α ± βi (resonanCE case). Consider the non-resonant case (among the roots of the characteristic polynomial is no root, equal to the number of α ± βi). Then the particular solution will search in the form y *(x) = exp(α x)(Pk (x)cos(β x) + Qk (x)sin(β x)), We consider the resonance case (among the roots of the characteristic polynomial is r roots equal to the number of α ± βi). Then the particular solution will be sought in the form y *(x) = exp(α x)(Pk (x)cos(β x) + Qk (x)sin(β x)) xr, Wronskian determinant. Liouville formula.
Wronskian determinant Given functions
where f (k) indicates the k th derivative of f (not exponentiation). The Wronskian of a set of functions
for some Therefore the Wronskian can be used to determine if functions are independent. This is useful in many situations. For example, if we wish to determine if two solution of a second- order differential equation are independent, we may use the Wronskian. Consider the functions x 2, x, and 1. Take the Wronskian:
Note that W is always non-zero, so these functions are independent everywhere. Consider, however, x 2 and x:
Note that W is always non-zero, so these functions are independent everywhere. Consider, however, x 2 and x:
Here W is always zero, so these functions are always dependent. This is intuitively obvious, of course, since 2 x 2+3=2(x 2)+3(1) Given n linearly independent functions
then As a simple illustration of this, let us consider polynomials of at most second order. Such a polynomial is a linear combination of
Hence, the equation is
Liouville formula. Definition. Let
Theorem (The Liouville formula) Let
for all Recall that the trace Proof. Let the entries of the matrix (
We use the following formula for differentiation of the determinant, which follows from the full expansion of the determinant and the product rule:
Indeed, if
Hence, when differentiating the full expansion of the determinant, each term of the determinant gives rise to n terms where one of the multiples is replaced by its derivative. Combining properly all such terms, we obtain the derivative of the determinant is the sum of n determinants where one of the rows is replaced by its derivative, that is, (1). The fact that each vector
|
||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 407; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.36.36 (0.008 с.) |

 (t),
(t),  (t), …,
(t), …,  (t)
(t) is called a fundamental system of solutions or basis.
is called a fundamental system of solutions or basis. has a fundamental system of solutions. If
has a fundamental system of solutions. If where
where  are arbitrary constants.
are arbitrary constants.
 and form a matrix of the order n x n
and form a matrix of the order n x n
 is linearly independent, then detY (t)= W (t)does not vanish for any value t of the interval of continuity of the matrix A (t). In this case the matrix Y (t) is called an integral or a fundamental matrix for the system
is linearly independent, then detY (t)= W (t)does not vanish for any value t of the interval of continuity of the matrix A (t). In this case the matrix Y (t) is called an integral or a fundamental matrix for the system  . If Y (
. If Y ( )= E, where E is the unit
)= E, where E is the unit , then the Wronskian determinant
, then the Wronskian determinant  is the determinant of the square matix
is the determinant of the square matix
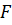 is another function, which is zero over any interval where
is another function, which is zero over any interval where 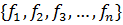 is also said to be dependent over an interval
is also said to be dependent over an interval 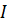 when there exists a non-trivial linear relation between them, i.e.,
when there exists a non-trivial linear relation between them, i.e.,
 , not all zero, at any
, not all zero, at any 



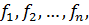 , we can use the Wronskian to construct a linear differential equation whose solution space is exactly the span of these functions. Namely, if g satisfies the equation;
, we can use the Wronskian to construct a linear differential equation whose solution space is exactly the span of these functions. Namely, if g satisfies the equation;
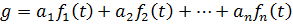 for some choice of
for some choice of 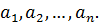
 and
and 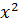 . We have
. We have
 which indeed has exactly polynomials of degree at most two as solutions.
which indeed has exactly polynomials of degree at most two as solutions. are
are  real-valued functions on
real-valued functions on  times differentiable on
times differentiable on 
 be a sequence of
be a sequence of 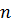 solutions of
solutions of  is continuous. Then the Wronskian
is continuous. Then the Wronskian 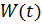 of this sequence satisfies the identity
of this sequence satisfies the identity
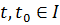 .
. trace A of the matrix A is the sum of all the diagonal entries of the matrix.
trace A of the matrix A is the sum of all the diagonal entries of the matrix. then
then

 are real-valued differentiable functions then the product rule implies by induction
are real-valued differentiable functions then the product rule implies by induction
 satisfies the equation
satisfies the equation  can be written in the coordinate form as follows
can be written in the coordinate form as follows



