
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Cauchy problem and the existence and uniqueness theoremСодержание книги
Поиск на нашем сайте
Bernoulli’s method Solution by using the change of variable(unknown function)of the form. y = uv, (2) where u = u (x), v = v (x) are differentiable functions in some domain of x. Differentiating (2) we get to the conclusion, that the general solution of the inhomogeneous linear differential equation (1) is equal to the sum of general solution of the corresponding homogeneous equation and a particular solution of the inhomogeneous equation (1) Yg.i=Yg.h+Yp.i Darboux equation is called the equation of the form: M (x, y) dx + N (x, y) dy + P (x, y)[ xdy − ydx ] = 0 (3), where M and N are homogeneous functions of degree m. P (x, y ) is a homogeneous function of degree l, l ≠ m −1 Darboux equation (3) can be integrated in quadrature with the substitution y = zx, where z is a new unknown function. With this change Darboux equation is reduced to equation with separated variables, if N (x, y) = 0. Cauchy problem and the existence and uniqueness theorem Existence theorem. If in the equation у’=ƒ(х,у) the function ƒ is defined and continuous in abounded domain D of the plane (x, y), then for any point (х0, у0)?D exists a solution y (x) of the initial problem dx/dy = f (x, y), у(х0)=у0, (4) defined on some interval containing х0. Existence and uniqueness theorem. If the function ƒ is defined and continuous in a bounded domain D of the plane (x, y), and it satisfies in D to Lipschitz condition in the variable y, i.e. | ƒ(х,у1)- ƒ(х,у2)| ≤ L|у2-у1|, (5) where, L is positive constant, then for any point (х0,у0)?D exists a unique solution у(х) of the initial problem (4), defined on some interval containing х0. Extension Theorem. At the conditions of the existence theorem or the theorem of the existence and uniqueness an any solution of the Cauchy problem (3.4) with initial data (х0,у0)?D can be extended to a point arbitrarily close to the boundary of D. In the first case, the continuation, in general, is not necessarily unique; in the second case it is unique.
4) Bernoulli’s method. Linear differential equation of the first order is an equation in which the unknown function and its first derivative are included in the first degree: Bernoulli’s method Solution by using the change of variable of the form. y = uv, (2) where u = u (x), v = v (x) are differentiable functions in some domain of x. Differentiating (2) we get to the conclusion, that the general solution of the inhomogeneous linear differential equation (1) is equal to the sum of general solution of the corresponding homogeneous equation and a particular solution of the inhomogeneous equation (1) Yg.i=Yg.h+Yp.i This fact is a reflection of the general properties of solutions of linear differential equations. Note that if you can "guess" a particular solution of (1), then the search for general solutions easy. Darboux equation is called the equation of the form: M (x, y) dx + N (x, y) dy + P (x, y)[ xdy − ydx ] = 0 (3) where M and N are homogeneous functions of degree m. P (x, y) is a homogeneous function of degree l, l ≠ m −1
5) Equations of the first order unsolved by derivatives. We consider the equation F (x, y, y’) = 0 (1) and suppose that it allows the parametric representation х=ϕ(u, v) у=ψ(u, v) (2) у'=α(u, v) so that F(ϕ(u, v),ψ(u, v),α(u, v)) ≡0, for all values of the parameters u and v. We assume, that the functions ϕ(u, v), ψ(u, v), α(u, v) are differentiable. Using the basic relation between the differentials and the derivative along the integral curves of the 1-st order dy=у’dx we find the connection between the parameters u and v. In fact, we have dx =
Equation (3) is the equation solved by derivative. In the equation (3) variables u and v are equal. Taking, for example, u as independent variable, and integrating equation (3), we obtain v = ω(u, c) which is general solution of (3).
Euler method. Given a complex- valued solution. It is proved that the real and imaginary parts of the complex - valued solution are solutions. the Euler method which is a method of constructing a fundamental system of solution for the equation Following Euler we find solution of the equation Equation 1) The roots of characteristic polynomial 2) The roots of characteristic polynomial are different, but among of them there are complex roots 3) The roots of characteristic equation are real, but among of them there multiple. In the 3rd case a theorem is proved. To multiple roots 4) In the general case can also be multiple complex roots. Note that is the multiplicity of the roots
15) Basic properties of linear systems. Vector and matrix form.
Linear System Matrix-Vector Form: given an nxn matrix A(t) and nx1 vector valued function f(t):
where aik(t),fi(t) are given functions, xi(t)is unknown functions called a linear system of differential equations. We denote
Then (1) takes the form If f(t)=0, the system is homogeneous.if not-it’ll be inhomogeneous Basic properties of linear system: Homogeneous System Solution Properties: -Linear combinations of solutions: if x1(t),x2(t),…xk()t,are solutions to x’=Ax,where x’=dx/dt, then x(t)=C1x1(t)+….+Ckxk(t), is also solution for any constants C1,…Ck. -independence:suppose y1(t),y2(t),…yk(t), are solutions to y’=Ay,for tє I=(a,b) a)if y1(t0)..yk(to) are dependent for some t0 є I,then there is exist C1,C2…Ck,not all 0,so that C1y1(t)+C2y2(t)+….+Ck yk (t)=0 (the yi(t)'s are dependent any t є I); b) if y1(t0)..yk(to) are dependent for some t0 є I,then yi(t)'s are dependent any t є I). -Solution Structure: if y1(t)….yn(t),are linearly independent solutions to the n-dimensioanl system y’=Ay, then any solution has the form y(t)= C1y1(t)+C2y2(t)+….+Cnyn (t) for some constants C1,C2….Cn. The n yi's form a fundamental set of solutions. - Solution Strategy: a)find n independent yi's to form general solution; b) if initial value y(t0) is given, solve Y(to)C=y(t0) for C=(C1,C2….Cn)T, using nxn matrix we have Wronskian
y21….. y2n the wronskian …. Yn1….. ynn
Orbital stability The orbital stability differs from the Lyapunov stabilities in that it concerns with the stability of a system output (or state) trajectory under small external perturbations. n Let f(x) be a p-periodic solution, p>0, of the autonomous system x(t)=f(x), x(t0)=x0?۠۠۠R and let Г represent the closed orbit of f(x) in the state space, namely, Г={y|y=f(x0),0≤t<p} If, for any e>0, there exists a constant b=b(e)>0 such that d(x0, Г):=inf||x0-y||<b the solution of the system, f(x) satisfies d(f(x), Г) < e, for all t≥t0 then this p-periodic solution trajectory, f(x) is said to be orbitally stable.
The main Lyapunov theorems. Basic theorem of Lyapunov Let V(x,t) be a non-negative function with derivative V’ along the trajectories of the system. 1.If V(x,t) is locally positive definite and V’(x,t) ≤0 locally in x and for all t, then the origin of the system is locally stable(in the sense of Lyapunov) 2.If V(x,t) is locally positive definite and decrescent,and V’(x,t) ≤0 locally in x and for all t, then the origin of the system is uniformly locally stable(in the sense of Lyapunov) 3. If V(x,t) is locally positive definite and decrescent, and -V’(x,t) ≤0 locally positive definite, then the origin of the system is uniformly locally asymptotically stable 4.If V(x,t) is locally positive definite and decrescent, and -V’(x,t) ≤0 locally positive definite, then the origin of the system is uniformly locally asymptotically stable Theorem. Exponential stability theorem x*=0 is an exponentially stable equilibrium point of x’=f(x,t) if and only if there exists an e>0 and a function V(x,t) which satisfies
29.Chetaev theorem nn n Theorem. [adapted from Chetaev 1934].Suppose E? R is open, 0? E, f;E→R and V: E→R are continuously differentiable, f(0)=0, V(0)=0. Suppose U an open neighborhood of 0 with compact closure F=U?E such that the restriction of V’=(DV)f to F∩V pow-1(0,∞) is strictly positive. If for every open neighborhood W?R pow n of 0 the set W∩W pow -1 (0,∞) is nonempty, then the origin is an unstable equilibrium of x’=f(x). Proof: 1.Assume above hypotheses 2.Let W be an open neighborhood of 0?R pow n 3There exists z?W∩V pow -1(0,∞).Define a=V(z)>0 4.The set K=F∩ V pow -1[a,∞) is compact, and it is nonempty since z?K 5Using the contiuity of V and V’ there exist m=minV’(x) and M=maxV(x) 6 Since K=F∩ V pow -1[a,∞)? F∩ V pow -1[a,∞) it follows that m>0 7 Let I? [0,∞) be the maximum interval of existence for empty set:I→E such that empty(0)=z 8 Define the set T={t? I: for all s?[0,t], empty set(s)=K } 9.For all t? T d/dt(V*empty set)(t)=(V’*empty set)(t)>m 10Hence for all t? T V(empty set(t))=V(empty set(0))+∫V(empty(s))ds≥a+mt 11 Since V is bounded above by M,T is also bounded above.Let t0 the least bounded of T. 12 Since K?E,I [0,t0] and empty(t0) is well-defined. Moreover t0 lies in the interior of I. 13 Since for all t?[0,t0),empty(t0)?K and for every b>0 there exist t?I,t0<t<t0+b such that it follows that empty(t0) lies on the boundary of the set K. 14 The boundary of K is contained in the union ӘK?V pow -1(a)U (F\U) 15 Since V(empty(t0))>a+m*t0>a it follows that empty(t0)? not V(a)pow -1 16 Therefore empty(t0)?(F\U) and in particular empty(t0)? not U 17 Since W was arbitrary this shows that the origin is an unstable equilibrium point of f.
Local and global theorems. Theorem. For any point Proof. The linear vector-function (t, x) By construction, Theorem. (global existence theorem). A linear system on a Riemann surface T admits a fundamental solution in any simply connected subdomain Proof. Choose a base point Since Assume that Agree on the intersections:
the solution can be explicitly constructed:
This completes the proof of existence of analytic continuation of solutions along paths.
Liouville formula. Definition. Let
Theorem (The Liouville formula) Let
for all Recall that the trace Proof. Let the entries of the matrix (
We use the following formula for differentiation of the determinant, which follows from the full expansion of the determinant and the product rule:
Indeed, if
Hence, when differentiating the full expansion of the determinant, each term of the determinant gives rise to n terms where one of the multiples is replaced by its derivative. Combining properly all such terms, we obtain the derivative of the determinant is the sum of n determinants where one of the rows is replaced by its derivative, that is, (1). The fact that each vector
Liouville formula. Theorem (The Liouville formula) Let
for all Recall that the trace Proof. Let the entries of the matrix (
We use the following formula for differentiation of the determinant, which follows from the full expansion of the determinant and the product rule:
Indeed, if
Hence, when differentiating the full expansion of the determinant, each term of the determinant gives rise to n terms where one of the multiples is replaced by its derivative. Combining properly all such terms, we obtain the derivative of the determinant is the sum of n determinants where one of the rows is replaced by its derivative, that is, (1). The fact that each vector
Bernoulli’s method Solution by using the change of variable(unknown function)of the form. y = uv, (2) where u = u (x), v = v (x) are differentiable functions in some domain of x. Differentiating (2) we get to the conclusion, that the general solution of the inhomogeneous linear differential equation (1) is equal to the sum of general solution of the corresponding homogeneous equation and a particular solution of the inhomogeneous equation (1) Yg.i=Yg.h+Yp.i Darboux equation is called the equation of the form: M (x, y) dx + N (x, y) dy + P (x, y)[ xdy − ydx ] = 0 (3), where M and N are homogeneous functions of degree m. P (x, y ) is a homogeneous function of degree l, l ≠ m −1 Darboux equation (3) can be integrated in quadrature with the substitution y = zx, where z is a new unknown function. With this change Darboux equation is reduced to equation with separated variables, if N (x, y) = 0. Cauchy problem and the existence and uniqueness theorem Existence theorem. If in the equation у’=ƒ(х,у) the function ƒ is defined and continuous in abounded domain D of the plane (x, y), then for any point (х0, у0)?D exists a solution y (x) of the initial problem dx/dy = f (x, y), у(х0)=у0, (4) defined on some interval containing х0. Existence and uniqueness theorem. If the function ƒ is defined and continuous in a bounded domain D of the plane (x, y), and it satisfies in D to Lipschitz condition in the variable y, i.e. | ƒ(х,у1)- ƒ(х,у2)| ≤ L|у2-у1|, (5) where, L is positive constant, then for any point (х0,у0)?D exists a unique solution у(х) of the initial problem (4), defined on some interval containing х0. Extension Theorem. At the conditions of the existence theorem or the theorem of the existence and uniqueness an any solution of the Cauchy problem (3.4) with initial data (х0,у0)?D can be extended to a point arbitrarily close to the boundary of D. In the first case, the continuation, in general, is not necessarily unique; in the second case it is unique.
4) Bernoulli’s method. Linear differential equation of the first order is an equation in which the unknown function and its first derivative are included in the first degree: Bernoulli’s method Solution by using the change of variable of the form. y = uv, (2) where u = u (x), v = v (x) are differentiable functions in some domain of x. Differentiating (2) we get to the conclusion, that the general solution of the inhomogeneous linear differential equation (1) is equal to the sum of general solution of the corresponding homogeneous equation and a particular solution of the inhomogeneous equation (1) Yg.i=Yg.h+Yp.i This fact is a reflection of the general properties of solutions of linear differential equations. Note that if you can "guess" a particular solution of (1), then the search for general solutions easy. Darboux equation is called the equation of the form: M (x, y) dx + N (x, y) dy + P (x, y)[ xdy − ydx ] = 0 (3) where M and N are homogeneous functions of degree m. P (x, y) is a homogeneous function of degree l, l ≠ m −1
5) Equations of the first order unsolved by derivatives. We consider the equation F (x, y, y’) = 0 (1) and suppose that it allows the parametric representation х=ϕ(u, v) у=ψ(u, v) (2) у'=α(u, v) so that F(ϕ(u, v),ψ(u, v),α(u, v)) ≡0, for all values of the parameters u and v. We assume, that the functions ϕ(u, v), ψ(u, v), α(u, v) are differentiable. Using the basic relation between the differentials and the derivative along the integral curves of the 1-st order dy=у’dx we find the connection between the parameters u and v. In fact, we have dx =
Equation (3) is the equation solved by derivative. In the equation (3) variables u and v are equal. Taking, for example, u as independent variable, and integrating equation (3), we obtain v = ω(u, c) which is general solution of (3).
|
||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 222; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.49.143 (0.009 с.) |

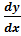 + p(x)y = q(x) (1)
+ p(x)y = q(x) (1)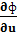 du+
du+  dv dy=
dv dy=  du+
du+  dv = α(u, v)[
dv = α(u, v)[ 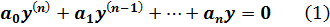
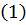 in the form
in the form  , where
, where  is a constant. We prove that equation
is a constant. We prove that equation 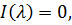 Where
Where 
 is called characteristic for
is called characteristic for 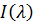 are real and different.
are real and different.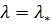 multiplicity ‘”k” corresponding to “k” linearly independent solution of the form
multiplicity ‘”k” corresponding to “k” linearly independent solution of the form 
 , that multiplicity of the adjoint root as well e. therefore, such pair of roots corresponding to the following linearly independent solutions
, that multiplicity of the adjoint root as well e. therefore, such pair of roots corresponding to the following linearly independent solutions 

 =
=  aik(t)xk+fi(t) i=1….n ( pustoi kvadrattyn ornynda ewtene jok)
aik(t)xk+fi(t) i=1….n ( pustoi kvadrattyn ornynda ewtene jok)
 =A(t)
=A(t)  +
+ 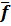 (t)
(t) t? I
t? I y11….. y1n this expression called
y11….. y1n this expression called


 T there exists a fundamental matrix solution
T there exists a fundamental matrix solution  defined in some small neighborhood U of
defined in some small neighborhood U of  .
.
 is holomorphic everywhere on T ×
is holomorphic everywhere on T × 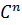 . By the local existence theorem, for any initial condition (
. By the local existence theorem, for any initial condition ( )
)  T ×
T × 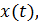 defined on some neighborhood of
defined on some neighborhood of  . Choose n solutions satisfying n linear independent initial conditions at
. Choose n solutions satisfying n linear independent initial conditions at  , hence the holomorphic matrix
, hence the holomorphic matrix 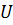 of the point
of the point 

 and let
and let  be a local fundamental matrix solution at this point. We extend it to an arbitrary point
be a local fundamental matrix solution at this point. We extend it to an arbitrary point  .
. is connected, there exists a compact piecewise smooth curve (path) γ connecting
is connected, there exists a compact piecewise smooth curve (path) γ connecting  . γ can be covered by
. γ can be covered by  carrying the respective local fundamental matrix solutions
carrying the respective local fundamental matrix solutions  , such that
, such that  are connected, and
are connected, and  if and only if |i − j|
if and only if |i − j|  1.
1.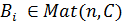 satisfy
satisfy  ,
,  ,
, 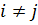 . Then
. Then  ,
, 
 ,
, 

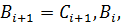
 .
. are
are  real-valued functions on
real-valued functions on 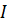 , which are
, which are  times differentiable on
times differentiable on 
 be a sequence of
be a sequence of 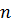 solutions of
solutions of  is continuous. Then the Wronskian
is continuous. Then the Wronskian 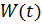 of this sequence satisfies the identity
of this sequence satisfies the identity
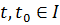 .
. trace A of the matrix A is the sum of all the diagonal entries of the matrix.
trace A of the matrix A is the sum of all the diagonal entries of the matrix. then
then

 are real-valued differentiable functions then the product rule implies by induction
are real-valued differentiable functions then the product rule implies by induction
 satisfies the equation
satisfies the equation  can be written in the coordinate form as follows
can be written in the coordinate form as follows



