
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Магнитное напряжение воздушного зазораСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте В воздушном заряде большая часть главного магнитного потока сосредоточена между полюсным наконечником и ротором(якорем). Предположим, что якорь не имеет зубцов и зазор по всей ширине полюсного наконечника постоянный. Тогда под полюсным наконечником магнитный поток в зазоре распределяется равномерно, а магнитная индукция по всей его ширине будет иметь постоянное значение
где bпн – истинная ширина полюсного наконечника;
Для полюсных наконечниках со скошенными краями принимают b Если зазор по ширине полюсного наконечника не одинаковый, то эквивалентный зазор равен
где
Отношение Длина якоря la равна длине полюса lп или принимается на 5…10 мм больше. В последним случаи уменьшаются потери на вихревые токи в торцевых частях машины.
С достаточной точностью можно считать, что
где lca=(la-nkbk) – суммарная длина пакетов; nk – число каналов; bk – ширина вентиляционных каналов(обычно bk=10мм).
Магнитная индукция в зазоре равна
Тогда Данная формула справедлива для гладкого якоря. Для якоря, который имеет зубцы, магнитное напряжение определяется по формуле
Отношение С учетом этого Произведение
где
В тех случаях, когда зубцовое строение имеет статор и ротор, коэффициент воздушного зазора определяется как для статора, так и для ротора ( В тех случаях, когда крепление обмотки якоря производится с помощью бандажей, которые укладываются в кольцевые канавки на внешней поверхности якоря, воздушный зазор по длине машины приобретает ступенчатую форму. При расчетах учет влияния бандажных канавок производится с помощью коэффициента
Результирующий коэффициент воздушного зазора равен
где
Магнитное напряжение зубцов t1=bп1+bz1– зубцовое деление Магнитный поток входит в якорь по двум параллельным путям, через зубцы и пазы. На протяжении полюса все зубцы в магнитном поле находятся в одинаковых условиях, поэтому для расчета можно рассматривать одно зубцовое деление. Для сечения на расстоянии х от поверхности якоря Фt=Фzx+Фпх
где Фt_– поток на одно зубцовое деление; Фzx– поток зубца в данном сечении; Фпх– поток в пазу в том же сечении.
Поток на одно зубцовое деление
Фt=
Распределение Фt между зубцом и пазом происходит обратно пропорционально их магнитным сопротивлениям. Если сталь зубца не насыщена, то его магнитное сопротивление во много раз меньше, чем магнитное сопротивление паза, поэтому можно считать, что весь поток идет через зубец
Фt=Фzx= Разделим это уравнение на площадь зубца в сечении х Bzx= где Вzx= Szx=bzxlcaKc– площадь зубца в том же сечении; Кс – коэффициент заполнения пакетов сталью(учитывает изоляцию между листами), Кс= Обычно Кс=0,91…0,93. Для определения напряженности магнитного поля в зубце Нzx используется кривая намагничивания стали В=f(H), из которой сделан сердечник якоря. Для сердечников современных ЭМ используется холоднокатаная изотропная электротехническая сталь марок 2013, 2312, 2411.
Магнитную индукцию Вzx можно определять по формуле до Вzx≤1,8 Тл. При больших значениях Вzx>1.8 Тл происходит насыщение стали зубца, его магнитное сопротивление возрастает и часть потока вытесняется в паз. В этом случае индукция в зубце определяется по формуле Фt=Фzx+Фпх. Поделим это уравнение на площадь зубца Szx в сечении х
Величина
где Sпх, Впх– площадь паза и индукция в сечении х; Нпх – напряженность магнитного поля; Кпх– коэффициент определяемый размерами паза и зубца в сечении х. Пазы и зубцы в сечении х находятся на одном уровне, поэтому Нzx=Hпх. Тогда
Вtx=Bzx+
Это нелинейное уравнение, запишем его в виде
Вzx=Btx–
В пособиях по проектированию ЭМ приводится зависимость Вt=f(Hz) при различных значениях Кп.По расчетной индукции Вtx можно определить напряженность
Нz=(Нz1 +4 Нz2 + Нz3) Магнитное напряжение зубца Fz=2Hzhz. Иногда используется формула
Fz=2HZ 1/3 hz,
где HZ 1/3 – напряженность поля на расстоянии
Овальные пазы Большую часть на высоте зубцы имеют одинаковое сечение. Можно принять, что Bzx по высоте зубца остается постоянной и Hzx=Hz и определяется для одного среднего сечения. Если полюсные наконечники имеют зубчатое строение, то эта часть магнитной цепи рассчитывается аналогично зубцовой зоне якоря.
|
||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 607; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.008 с.) |

 . В межполюсном промежутке магнитное сопротивление очень велико и индукция падает, уменьшаясь до нуля в середине между полюсными наконечниками. Для расчетов принимают распределения магнитной индукции
. В межполюсном промежутке магнитное сопротивление очень велико и индукция падает, уменьшаясь до нуля в середине между полюсными наконечниками. Для расчетов принимают распределения магнитной индукции  в зазоре принимают прямоугольным высотой
в зазоре принимают прямоугольным высотой  .При этом площади трапеции????????
.При этом площади трапеции????????  – расчетная индукция и расчетная ширина полюсного наконечника. Расчетную ширину полюсного наконечника определяют по формуле
– расчетная индукция и расчетная ширина полюсного наконечника. Расчетную ширину полюсного наконечника определяют по формуле .
.
 – зазор в середине полюсного наконечника;
– зазор в середине полюсного наконечника; – зазор по краям,
– зазор по краям,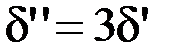 .
. – коэффициент полюсного перекрытия. Обычно
– коэффициент полюсного перекрытия. Обычно 
 За расчетную длину якоря принимаются основания прямоугольника
За расчетную длину якоря принимаются основания прямоугольника  , который имеет высоту
, который имеет высоту  и площадь, равную площади по действительной кривой поля.
и площадь, равную площади по действительной кривой поля. ),
),
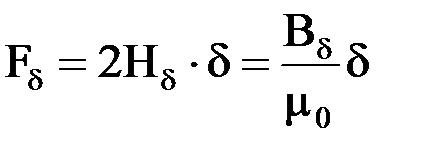 .
.
 - коэффициент воздушного зазора. Коэффициент
- коэффициент воздушного зазора. Коэффициент  >1 и возрастает с увеличением раскрытия паза.
>1 и возрастает с увеличением раскрытия паза.
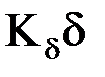 – эквивалентный воздушный зазор. Коэффициент воздушного зазора определяется по формуле
– эквивалентный воздушный зазор. Коэффициент воздушного зазора определяется по формуле
 – зубчатое деление якоря;
– зубчатое деление якоря; – ширина зубца по окружности якоря;
– ширина зубца по окружности якоря;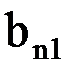 – ширина открытия паза у поверхности воздушного зазора.
– ширина открытия паза у поверхности воздушного зазора. ). При этом t1 bz1 принимаются соответственно по размерам зубцов и пазов статора и ротора.
). При этом t1 bz1 принимаются соответственно по размерам зубцов и пазов статора и ротора. , который определяется по формуле
, который определяется по формуле ,
, где
где  - число бандажных канавок.
- число бандажных канавок. .
.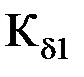 - коэффициент воздушного зазора статора;
- коэффициент воздушного зазора статора; - коэффициент воздушного зазора ротора;
- коэффициент воздушного зазора ротора; - коэффициент воздушного зазора для бандажных канавок.
- коэффициент воздушного зазора для бандажных канавок.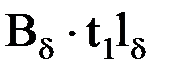

 ,
, – индукция в сечении х зубца;
– индукция в сечении х зубца; , где lc– длина чистой стали в пакете;
, где lc– длина чистой стали в пакете;  –длина пакета.
–длина пакета. Ранее применялась горячекатаная сталь марок 1211, 1212, 1311, 1411 и др.
Ранее применялась горячекатаная сталь марок 1211, 1212, 1311, 1411 и др.
 называется расчетной индукцией в сечении зубца. Первое слагаемое – действительная индукция Вzx в том же сечении. Второе слагаемое можно представить
называется расчетной индукцией в сечении зубца. Первое слагаемое – действительная индукция Вzx в том же сечении. Второе слагаемое можно представить =ВпхКпх=
=ВпхКпх= 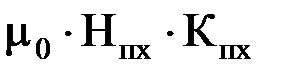 ,
, .
. ,
, И воспользуемся графическим решением. Строится кривая намагничивания В=f(H).Для сечения х зубца определяется расчетная индукция Вzx=
И воспользуемся графическим решением. Строится кривая намагничивания В=f(H).Для сечения х зубца определяется расчетная индукция Вzx= 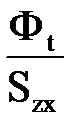 и откладывается на оси ординат. Из точки проводится прямая АС, ординат которой равны Btx–
и откладывается на оси ординат. Из точки проводится прямая АС, ординат которой равны Btx–  . Пересечение прямой Ас с кривой намагничивания дает значение действительной индукции в зубце Вzx и соответствующую ей напряженность магнитного поля
. Пересечение прямой Ас с кривой намагничивания дает значение действительной индукции в зубце Вzx и соответствующую ей напряженность магнитного поля  .
. Трапециидальная форма зубца. Площадь сечения по высоте зубца изменяется. Индукция тоже изменяется. Напряженность тоже. Чтобы определить расчетное значение Нz проводится расчет для ряда точек по высоте зубца (обычно три точки в верхнем, нижнем и среднем сечении).Для каждого сечения определяется расчетная индукция Btx, а по ней напряженность определяется непосредственно по кривой намагничивания стали. При Вzx >1,8 Тл – по одной из кривых, подобных тем, какие приводятся в пособиях по расчету ЭМ(требуемая кривая выбирается по коэффициенту Кпх). По полученным данным строится кривая изменения
Трапециидальная форма зубца. Площадь сечения по высоте зубца изменяется. Индукция тоже изменяется. Напряженность тоже. Чтобы определить расчетное значение Нz проводится расчет для ряда точек по высоте зубца (обычно три точки в верхнем, нижнем и среднем сечении).Для каждого сечения определяется расчетная индукция Btx, а по ней напряженность определяется непосредственно по кривой намагничивания стали. При Вzx >1,8 Тл – по одной из кривых, подобных тем, какие приводятся в пособиях по расчету ЭМ(требуемая кривая выбирается по коэффициенту Кпх). По полученным данным строится кривая изменения  .
. hz от основания зубца.
hz от основания зубца.


