
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчет магнитной цепи при холостом ходе.Содержание книги
Поиск на нашем сайте
Расчет магнитной цепи при холостом ходе.
В электрических машинах магнитный поток подразделяется на главный поток и поток рассеяния. Главный поток замыкается по отдельным участкам стартера и ротора, которые составляют магнитную цепь машины. Главный магнитный поток выбирают исходя из того, что, чтобы он идуцировал в обмотках заданную ЭДС. МДС, необходимая для создания такого потока определяется из расчета магнитной цепи При холостом ходе эту МДС создаёт одна из обмоток при протекании по ней тока. В синхронных машинах такой обмоткой является обмотка возбуждения, в МПТ тоже, в АД – обмотка статора.
Здесь одна пара полюсов Ф – основной магнитный поток; Фб – магнитный поток рассеяния; Главный магнитный поток замыкается по нескольким замкнутым контурам. Т.к. все контуры одинаковы, то расчет магнитной цепи выполняется для одного из них. В результате определяется МДС пары полюсов. Расчет магнитной цепи выполняется на основе закона полного тока. Для контура основного магнитного потока для пары полюсов запишем
где Fв – МДС возбуждения; Iв, ωв – ток и число витков на полюсе обмотки возбуждения; Н – напряженность магнитного поля; l – длина контура интегрирования.
При практических расчетах интеграл заменяют суммой магнитных напряжений Нl, для чего магнитную цепь машины разбивают на участки, в каждом из которых можно принять, что индукция В И напряженность магнитного поля Н имеют неизменное значение. В соответствии с рисунком такие участки являются воздушный заряд, зубцы якоря, ярмо якоря, полюсы, ярмо статора. Длина силовой линии потока Ф на каждом из участков обозначена:
аb –
Тогда вместо интегрального выражения получим
где магнитные напряжения участков. Расчет магнитной цепи заключается в определении напряженности магнитного поля, а затем магнитного напряжения для каждого участка магнитной цепи. Напряженность магнитного поля находится по соответствующему значению магнитной индукции.
Магнитное напряжение зубцов
t1=bп1+bz1– зубцовое деление Магнитный поток входит в якорь по двум параллельным путям, через зубцы и пазы. На протяжении полюса все зубцы в магнитном поле находятся в одинаковых условиях, поэтому для расчета можно рассматривать одно зубцовое деление. Для сечения на расстоянии х от поверхности якоря Фt=Фzx+Фпх
где Фt_– поток на одно зубцовое деление; Фzx– поток зубца в данном сечении; Фпх– поток в пазу в том же сечении.
Поток на одно зубцовое деление
Фt=
Распределение Фt между зубцом и пазом происходит обратно пропорционально их магнитным сопротивлениям. Если сталь зубца не насыщена, то его магнитное сопротивление во много раз меньше, чем магнитное сопротивление паза, поэтому можно считать, что весь поток идет через зубец
Фt=Фzx= Разделим это уравнение на площадь зубца в сечении х Bzx= где Вzx= Szx=bzxlcaKc– площадь зубца в том же сечении; Кс – коэффициент заполнения пакетов сталью(учитывает изоляцию между листами), Кс= Обычно Кс=0,91…0,93. Для определения напряженности магнитного поля в зубце Нzx используется кривая намагничивания стали В=f(H), из которой сделан сердечник якоря. Для сердечников современных ЭМ используется холоднокатаная изотропная электротехническая сталь марок 2013, 2312, 2411.
Магнитную индукцию Вzx можно определять по формуле до Вzx≤1,8 Тл. При больших значениях Вzx>1.8 Тл происходит насыщение стали зубца, его магнитное сопротивление возрастает и часть потока вытесняется в паз. В этом случае индукция в зубце определяется по формуле Фt=Фzx+Фпх. Поделим это уравнение на площадь зубца Szx в сечении х
Величина
где Sпх, Впх– площадь паза и индукция в сечении х; Нпх – напряженность магнитного поля; Кпх– коэффициент определяемый размерами паза и зубца в сечении х. Пазы и зубцы в сечении х находятся на одном уровне, поэтому Нzx=Hпх. Тогда
Вtx=Bzx+
Это нелинейное уравнение, запишем его в виде
Вzx=Btx–
В пособиях по проектированию ЭМ приводится зависимость Вt=f(Hz) при различных значениях Кп.По расчетной индукции Вtx можно определить напряженность
Нz=(Нz1 +4 Нz2 + Нz3) Магнитное напряжение зубца Fz=2Hzhz. Иногда используется формула
Fz=2HZ 1/3 hz,
где HZ 1/3 – напряженность поля на расстоянии
Овальные пазы Большую часть на высоте зубцы имеют одинаковое сечение. Можно принять, что Bzx по высоте зубца остается постоянной и Hzx=Hz и определяется для одного среднего сечения. Если полюсные наконечники имеют зубчатое строение, то эта часть магнитной цепи рассчитывается аналогично зубцовой зоне якоря. Добавочные потери. Добавочные потери магнитные потери, которые обусловлены зубчатым строением сердечника. Подразделяются на поверхностные и пульсационные. Поверхностные потери возникают в полюсах или зубцах в следствии пульсации индукции на их поверхности при перемещении ротора относительно статора. Частота пульсаций равна fz= Пульсационные потери возникают в машинах, имеющих зубцы на статоре и роторе. При изменении взаимного расположения зубцов статора и ротора при вращении в них происходит изменение потока, что вызывает появление добавочных потерь во всем объеме зубцов. Механические потери. Механические потери состоят из потерь на трение щеток о коллектор или кольца, потерь на трения в подшипниках и вентиляционных потерь. Потеря на трение щеток о коллектор и кольца вычисляют по формуле
Ртрщ=Ктр∙fщ∙Sщ∙υк,
где Ктр – коэффициент трения щеток о коллектор или кольца, принимается Ктр=0,25; fщ – давление на щётку(в среднем принимается fщ ≈(15…25)∙103 Па); Sщ – суммарная площадь контактов всех щеток, м2; υк – окружная скорость коллектора, м/с. Потери в подшипниках зависит от их конструкции, состояния трущихся поверхностей и применяемой смазки. Для машин малой и средней мощности применяются шариковые или роликовые подшипники с консистентной смазкой в крупных машинах применяются подшипники скольжения с принудительной смазкой.
Коэффициенты трения для различных видов подшипников находятся из справочников. Вентиляционные потери зависят от конструкции машины и от типа применяемого вентилятора. В машинах с самовентиляцией это потери пропорциональны квадрату скорости по внешнему диаметру вентилятора. Электрические потери в щеточном контакте определяются по формуле
Рэщ=
Переходные падения напряжения для угольных и графитных щеток – для металлоугольных и металлографитных щеток – При расчетах принимается, что Поперечная реакция якоря Поперечная реакция якоря МПТ Реакция якоря – это воздействие поля якоря на поле возбуждения. Рассмотрим реакции якоря, когда щетки установлены на геометрической нейтрали. Магнитное поле возбуждения в МПТ при отсутствии поля якоря на первом рисунке. На втором рисунке магнитное поле якоря при отсутствии поля возбуждения. Оно неподвижное, т.к.распределение тока по проводникам якоря сохраняется постоянным при вращении якоря. Это поле якоря называемое полем поперечной реакции якоря.
Сделаем допущение, что якорь не имеет зубцов, а проводники обмотки якоря равномерно распределены по его окружности. Через каждый из N проводников обмотки якоря протекает ток параллельной ветви ia=
А=
где Da – внешний диаметр якоря;
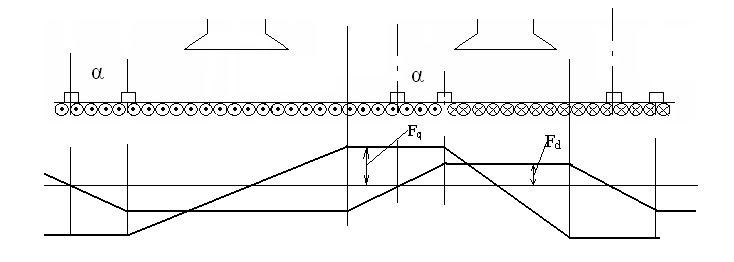
Линейная нагрузка изменяется от 5 до 70 Развернем статор и якорь МПТ в плоскость. За начало отсчета принята точка О, лежащая на поверхности якоря и на оси полюса. Ось полюса является линией симметрии для потока поперечной реакции. На расстоянии х от этой линии проведем одну из индукционных линий якоря. Полный ток, охватываемый её будет равен 2х∙А=2Fqx. Величина 2Fqx=2х∙А представляет собой МДС поперечной реакции якоря на один зазор. При х=0 Fqx=0, с увеличением х МДС поперечной реакции якоря возрастает, достигая максимального значения при х=
Fq=
При х> МДС поперечной реакции якоря можно записать в виде суммы
Fqx=
где
Магнитное напряжение воздушного зазора (на один зазор)
где
Подставляем в уравнение для Fqx и решаем относительно
Предположим, что в стальных участках магнитной цепи Тогда
Магнитная индукция поля поперечной якоря в воздушном зазоре пропорциональна МДС
Выводы
1 при нагрузке машины под влиянием поперечной реакции якоря происходит искажение магнитного поля машины. Под одним краем полюса она ослабляется, под другим увеличивается. В генераторах ослабление поля происходит на набегающем крае полюса, в двигателях – на сбегающем крае полюса; 2 точки Ф и Ф/ (определяют положение физической нейтрали) смещаются относительно геометрической нейтрали. В генераторах точки Ф и Ф/ смещаются в сторону вращения якоря, в двигателях – против вращения якоря. Положение физической нейтрали зависит от нагрузки; 3 В насыщенных машинах нельзя получить результирующее магнитное поле путем простого сложения поля возбуждения и поля поперечной реакции якоря. Поэтому распределения магнитной индукции в воздушном зазоре под плюсом будет иным(пунктирная линия). Продольная реакция якоря. Иногда в машинах постоянного тока щетки устанавливаются со смещением на угол
Пространственное распределение обоих МДС имеет следующий вид. Выразим угловое смещение щеток через соответствующую дугу окружности якоря
d=
Тогда максимальное значение продольной реакции якоря будет равно
Fd= d∙A=
Максимальное значение МДС поперечной реакции якоря
Fq=(
Из приведенных формул следует, что при Продольная реакция якоря не искажает результирующее магнитное поле машины.
Расчет магнитной цепи при холостом ходе.
В электрических машинах магнитный поток подразделяется на главный поток и поток рассеяния. Главный поток замыкается по отдельным участкам стартера и ротора, которые составляют магнитную цепь машины. Главный магнитный поток выбирают исходя из того, что, чтобы он идуцировал в обмотках заданную ЭДС. МДС, необходимая для создания такого потока определяется из расчета магнитной цепи При холостом ходе эту МДС создаёт одна из обмоток при протекании по ней тока. В синхронных машинах такой обмоткой является обмотка возбуждения, в МПТ тоже, в АД – обмотка статора.
Здесь одна пара полюсов Ф – основной магнитный поток; Фб – магнитный поток рассеяния; Главный магнитный поток замыкается по нескольким замкнутым контурам. Т.к. все контуры одинаковы, то расчет магнитной цепи выполняется для одного из них. В результате определяется МДС пары полюсов. Расчет магнитной цепи выполняется на основе закона полного тока. Для контура основного магнитного потока для пары полюсов запишем
где Fв – МДС возбуждения; Iв, ωв – ток и число витков на полюсе обмотки возбуждения; Н – напряженность магнитного поля; l – длина контура интегрирования.
При практических расчетах интеграл заменяют суммой магнитных напряжений Нl, для чего магнитную цепь машины разбивают на участки, в каждом из которых можно принять, что индукция В И напряженность магнитного поля Н имеют неизменное значение. В соответствии с рисунком такие участки являются воздушный заряд, зубцы якоря, ярмо якоря, полюсы, ярмо статора. Длина силовой линии потока Ф на каждом из участков обозначена:
аb –
Тогда вместо интегрального выражения получим
где магнитные напряжения участков. Расчет магнитной цепи заключается в определении напряженности магнитного поля, а затем магнитного напряжения для каждого участка магнитной цепи. Напряженность магнитного поля находится по соответствующему значению магнитной индукции.
|
|||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 187; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.218.107 (0.009 с.) |

 Принцип расчета магнитной цепи всех машин одинаковы. Для примера рассмотрим явно полюсную машину, поперечный разрез которой представлен на рисунке.
Принцип расчета магнитной цепи всех машин одинаковы. Для примера рассмотрим явно полюсную машину, поперечный разрез которой представлен на рисунке.

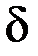 ; af – hz; fe – La; bc – hn; cd– Lc.
; af – hz; fe – La; bc – hn; cd– Lc.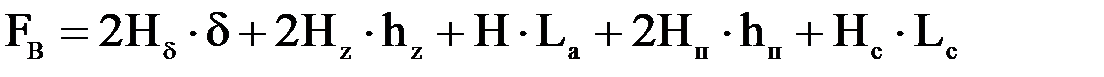 или
или
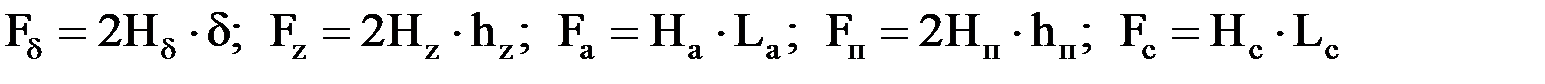 –
–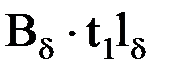

 ,
, – индукция в сечении х зубца;
– индукция в сечении х зубца; , где lc– длина чистой стали в пакете;
, где lc– длина чистой стали в пакете;  –длина пакета.
–длина пакета. Ранее применялась горячекатаная сталь марок 1211, 1212, 1311, 1411 и др.
Ранее применялась горячекатаная сталь марок 1211, 1212, 1311, 1411 и др.
 называется расчетной индукцией в сечении зубца. Первое слагаемое – действительная индукция Вzx в том же сечении. Второе слагаемое можно представить
называется расчетной индукцией в сечении зубца. Первое слагаемое – действительная индукция Вzx в том же сечении. Второе слагаемое можно представить =ВпхКпх=
=ВпхКпх= 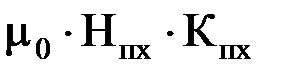 ,
, .
. ,
, И воспользуемся графическим решением. Строится кривая намагничивания В=f(H).Для сечения х зубца определяется расчетная индукция Вzx=
И воспользуемся графическим решением. Строится кривая намагничивания В=f(H).Для сечения х зубца определяется расчетная индукция Вzx= 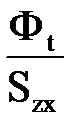 и откладывается на оси ординат. Из точки проводится прямая АС, ординат которой равны Btx–
и откладывается на оси ординат. Из точки проводится прямая АС, ординат которой равны Btx–  . Пересечение прямой Ас с кривой намагничивания дает значение действительной индукции в зубце Вzx и соответствующую ей напряженность магнитного поля
. Пересечение прямой Ас с кривой намагничивания дает значение действительной индукции в зубце Вzx и соответствующую ей напряженность магнитного поля  .
. Трапециидальная форма зубца. Площадь сечения по высоте зубца изменяется. Индукция тоже изменяется. Напряженность тоже. Чтобы определить расчетное значение Нz проводится расчет для ряда точек по высоте зубца (обычно три точки в верхнем, нижнем и среднем сечении).Для каждого сечения определяется расчетная индукция Btx, а по ней напряженность определяется непосредственно по кривой намагничивания стали. При Вzx >1,8 Тл – по одной из кривых, подобных тем, какие приводятся в пособиях по расчету ЭМ(требуемая кривая выбирается по коэффициенту Кпх). По полученным данным строится кривая изменения
Трапециидальная форма зубца. Площадь сечения по высоте зубца изменяется. Индукция тоже изменяется. Напряженность тоже. Чтобы определить расчетное значение Нz проводится расчет для ряда точек по высоте зубца (обычно три точки в верхнем, нижнем и среднем сечении).Для каждого сечения определяется расчетная индукция Btx, а по ней напряженность определяется непосредственно по кривой намагничивания стали. При Вzx >1,8 Тл – по одной из кривых, подобных тем, какие приводятся в пособиях по расчету ЭМ(требуемая кривая выбирается по коэффициенту Кпх). По полученным данным строится кривая изменения  .
. hz от основания зубца.
hz от основания зубца.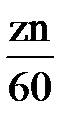 . Частота пульсаций значительная, поэтому индуцируемые полем вихревые токи и вызванные ими потери имеют малую глубину проникновения и возникают в?????79?? тонких слоях сердечников, обращенных к воздушному зазору. Отсюда названия поверхностные потери.
. Частота пульсаций значительная, поэтому индуцируемые полем вихревые токи и вызванные ими потери имеют малую глубину проникновения и возникают в?????79?? тонких слоях сердечников, обращенных к воздушному зазору. Отсюда названия поверхностные потери. Uщ∙Ia.
Uщ∙Ia. Uщ на пару щеток принимаются равным:
Uщ на пару щеток принимаются равным: Когда Ib≠0, в МПТ образуется результирующее магнитное поле. За счет равно поперечной реакции якоря происходит искажение магнитного поля в МПТ. Под одним краем полюса оно усиливается, под другим ослабляется. Чтобы выяснить картину поля в воздушном зазоре МПТ, найдем распределение МДС и индукции поперечной реакции якоря.
Когда Ib≠0, в МПТ образуется результирующее магнитное поле. За счет равно поперечной реакции якоря происходит искажение магнитного поля в МПТ. Под одним краем полюса оно усиливается, под другим ослабляется. Чтобы выяснить картину поля в воздушном зазоре МПТ, найдем распределение МДС и индукции поперечной реакции якоря.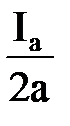 . Тогда МДС на единицу длины окружности якоря будет равна
. Тогда МДС на единицу длины окружности якоря будет равна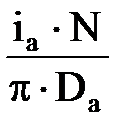 ,
, А – линейная нагрузка якоря, от которой зависят размеры и ряд характеристик МПТ.
А – линейная нагрузка якоря, от которой зависят размеры и ряд характеристик МПТ.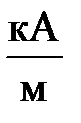 и увеличивается с возрастанием мощности машины.
и увеличивается с возрастанием мощности машины.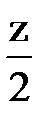 (в нейтрали)
(в нейтрали)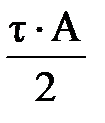 .
.
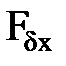 – магнитное напряжение, необходимое для проведения магнитного поля поперечной реакции якоря через воздушный зазор, расположенный у точки х поверхности якоря.
– магнитное напряжение, необходимое для проведения магнитного поля поперечной реакции якоря через воздушный зазор, расположенный у точки х поверхности якоря. – сумма магнитных напряжений стальных участков магнитной цепи вдоль половины линии потока якоря. Обычно
– сумма магнитных напряжений стальных участков магнитной цепи вдоль половины линии потока якоря. Обычно  .
.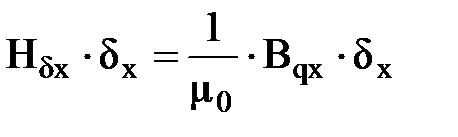 ,
,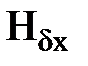 ,
,  – напряженность магнитного поля и индукция в воздушном зазоре на расстоянии х от оси полюса;
– напряженность магнитного поля и индукция в воздушном зазоре на расстоянии х от оси полюса; – воздушный зазор между полюсом и якорем на расстоянии х от оси полюса;
– воздушный зазор между полюсом и якорем на расстоянии х от оси полюса; – магнитная постоянная.
– магнитная постоянная.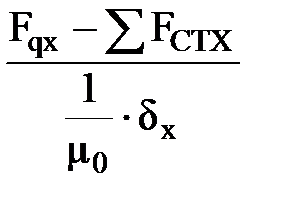
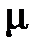 =
=  и
и  =0 (МПТ не насыщено).
=0 (МПТ не насыщено). .
.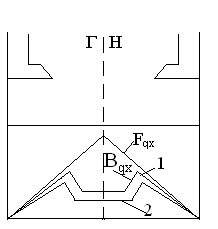
 и обратно пропорциональна воздушному зазору
и обратно пропорциональна воздушному зазору  . Т.к. под полюсом
. Т.к. под полюсом  – магнитная индукция поля возбуждения.
– магнитная индукция поля возбуждения.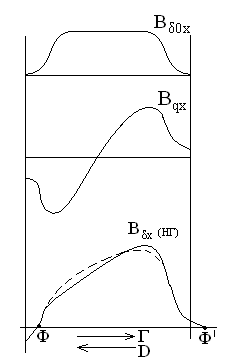
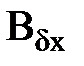 (НГ) –магнитная индукция результирующего поля.
(НГ) –магнитная индукция результирующего поля.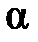 относительно геометрической нейтрали. МДС реакции якоря можно разложить на две составляющее: поперечную
относительно геометрической нейтрали. МДС реакции якоря можно разложить на две составляющее: поперечную 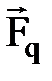 и продольную
и продольную 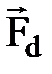 .
. Вектор МДС
Вектор МДС  направлен по геометрической нейтрали, а вектор МДС
направлен по геометрической нейтрали, а вектор МДС 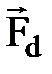 направлен по оси полюсов.
направлен по оси полюсов. .
.
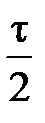 –d)∙A=(
–d)∙A=(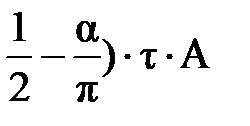 .
.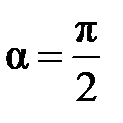 в машине будет существовать только продольная реакция якоря. Она направлена против поля возбуждения и оказывает размагничивающее действие. При смещении щеток в противоположную сторону(против направления вращения якоря в генераторах и по направлению вращения якоря в двигателях) продольная реакция якоря будет оказывать подмагничивающее действие.
в машине будет существовать только продольная реакция якоря. Она направлена против поля возбуждения и оказывает размагничивающее действие. При смещении щеток в противоположную сторону(против направления вращения якоря в генераторах и по направлению вращения якоря в двигателях) продольная реакция якоря будет оказывать подмагничивающее действие.


