
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Подобными называют такие явления, для которых отношения сходственных и характеризующих их величин постоянны.Содержание книги
Поиск на нашем сайте
Различают следующие виды подобия: а) геометрическое; б) временное; в) физических величин; г) начальных и граничных условий. Геометрическое подобие предполагает, что сходственные размеры натуры и модели параллельны, а их соотношение выражается постоянной величиной. Предположим, что изучается сложное явление – движение газа во вращающемся цилиндре (рис. 7.1). Чтобы исследовать процесс в данном аппарате, строим модель, соблюдая геометрическое подобие (рис. 7.1б), т.е. равенство отношений сходственных линейных размеров натуры и модели.
А2 А1 D2 D1 l 2 L2 l 1 б L1
а Рис. 7.1. К определению условий подобия натуры (а) и модели (б)
Если рассматриваемая система (натура, образец) находится в движении, то при наличии геометрического подобия все ее точки должны перемещаться по подобным траекториям сходственных точек подобной ей системы (модели), т.е. проходить геометрически подобные пути (точки А1 и А2). Геометрическое подобие соблюдается при равенстве отношений всех сходственных размеров и модели:
Безразмерную величину al называют константой геометрического подобияилимасштабным (переходным) множителем. Константа подобия характеризует отношение однородных сходственных величин в подобных системах и позволяет перейти от размеров одной системы (модели) к другой (натуре). Временное подобие предполагает, что сходственные точки или части геометрически подобных систем (натуры и модели), двигаясь по геометрически подобным траекториям, проходят геометрически подобные пути в промежутки времени, отношение которых является постоянной величиной: Т1/Т2 = где Т 1 и Т 2 – время прохождения сходственными частицами всего аппарата, натуры и модели соответственно; Подобие физических величин предполагает, что в рассматриваемых подобных системах (натуры и модели) отношение значений физических величин двух любых сходственных точек или частиц, подобно размещенных в пространстве и времени, есть величина постоянная. Например, если в натуре частица за время
где и 1 и и 2 – совокупность физических величин (но в общем случае а Подобие физических величин включает подобие не только физических констант, но и совокупности значений физических величин, или полей физических величин. Таким образом, при соблюдении геометрического и физического подобия будет также соблюдаться подобие скоростей, температур, концентраций и других физических величин. Подобие начальных и граничных условий предполагает, что начальное состояние и состояние граничных условий (натуры и модели) подобны, т.е. отношения основных параметров в начале и на границах системы постоянны. Это справедливо лишь в тех случаях, когда для начальных и граничных условий системы выдерживается геометрическое, физическое и временное подобия. Этим подчеркивается важность подобия начальных и граничных условий, поскольку иногда в основном объеме системы подобие может соблюдаться не полностью. Вместе с тем даже незначительное отклонение начальных и граничных условий может привести к существенному нарушению подобия системы в целом (например, неучет сильных возмущений всей системы в результате так называемых «входных эффектов»). Все константы подобия постоянны для различных сходственных точек подобных систем, но изменяются в зависимости от соотношения размеров натуры и модели. Иными словами, отношение однородных сходственных величин натуры и другой модели будет другим. Это обстоятельство представляет большие неудобства для масштабирования и преодолевается введением, так называемых, инвариантовподобия. Инварианты подобия и критерии подобия Если все сходственные величины, определяющие состояние данной системы (натуры) и подобной ей системы (модели), измерять в относительных единицах, т.е. брать сходственное отношение величин для каждой системы, то оно будет величиной постоянной и безразмерной, например: L1/D1 = L2/D2 =….= inv = idem = i l; T 1/ Величины il, i Инварианты подобия, выражающие отношение однородных величин, называются симплексами или параметрическими критериями, например, отношение L1/D1 – геометрический симплекс. Инварианты подобия, выраженные соотношением разнородных величин, называют критериями подобия. Обычно принято обозначать их именами ученых, внесших существенный вклад в данную область знаний (например Re – число или критерий Рейнольдса). Можно получить критерии для любого физического явления. Для этого необходимо иметь аналитическую зависимость между переменными величинами рассматриваемого явления. Критерии подобия безразмерны, их значения для каждой точки данной системы могут меняться. Но для сходственных точек подобных систем они не зависят от относительных размеров натуры и модели. Таким образом, явления, подобные между собой, характеризуются численно равными критериями подобия. Равенство критериев подобия – единственное условие подобия процессов. Отсюда очевидно, что отношение критериев одной системы к критериям другой, подобной ей системы, всегда равно 1. Если неизвестно исходное уравнение, описывающее данное явление (процесс), то для формирования критериев подобия можно использовать анализ размерностей – учение о методах рационального построения систем единиц измерения. При этом величины разделяют на первичные, численные значения которых определяют прямым измерением, и вторичные, определяемые как функции первичных. В основе метода анализа размерностей лежит Эта теорема связывает анализ размерностей с теорией подобия, поскольку при условии соблюдения подобия безразмерные комплексы, найденные с помощью Гидродинамическое подобие В соответствии с теорией подобия можно записать равенство:
силы массовые силы силы давления силы инерции вязкости
Здесь под каждым из комплексов записаны силы, за которые по смыслу уравнения Навье – Стокса «отвечают» соответствующие комплексы. Сравнивая попарно рассматриваемые эффекты (в принятой трактовке – силы), можно получить 6 равенств, из которых 3 являются независимыми и дают 3 «основные» обобщенныепеременные (остальные 3 равенства приводят к производным обобщенным переменным, которые могут быть также получены комбинацией трех основных). В настоящее время в качестве базы приняты силы инерции тw2/ml. Cопоставление сил инерции и давления. После сокращения на ml и подстановки значения множителей mp =p1 /p2, mp =
откуда, разведя величины с одинаковыми индексами в разные части равенства, получаем для всех подобных значений – в сходственных точках:
где Eu - критерий (число) Эйлера. Критерий Эйлера – это соотношение сил инерции и давления. В технологических процессах нас, как правило, интересует не давление р в какой-либо точке или сечении аппарата, а перепад давления Еu = Сопоставление массовых сил с силами инерции. После подстановки т м = Р1/Р2 (при этом вдоль оси z, если она направлена вертикально, речь может идти о единичной массовой силе тяжести, численно равной ее ускорению g), mw и ml имеем:
откуда, повторяя вышеприведенную операцию, получаем для всех подобных течений в сходственных точках:
где Fr - критерий (число) Фруда Смысл Fr – это соотношение массовых сил и сил инерции. Следует отметить, что разные источники дают разное написание критерия Фруда: gl/w2, w2/gl, w/ Сопоставление сил инерции и вязкости. После проведения операций, аналогичных вышеприведенным, имеем:
откуда, разводя величины с одинаковыми индексами в разные части равенства, получаем для всех подобных течений в сходственных точках:
т.к. v = Re = Смысл числа Рейнольдса, наиболее широко используемого из всех критериев переноса, ясен из названия процедуры сопоставления: это соотношение сил инерции и сил вязкости. Конкретные значения Re, отвечающие преобладанию тех или иных сил, зачастую можно установить только экспериментально. Можно лишь утверждать, что увеличение Re означает относительное возрастание сил инерции, а уменьшение – возрастание сил вязкости (внутреннего трения). Для потоков жидкости, движущихся по прямым трубопроводам, Re зависит от режима движения потока (рис.7.2). Для потоков жидкости, проходящих по изогнутым трубам (змеевикам), значение Re возрастает и зависит от соотношения d/D, где d – внутренний диаметр трубки змеевика; D – диаметр витков змеевика. Для потоков, движущихся в трубах некруглого сечения, в качестве линейного размера принимается значение эквивалентного диаметра, который равен учетверенному гидравлическому радиусу d экв = 4 r экв, где r экв = S/П =
a) б) c) Ламинарный переходный турбулентный режим режим режим Re <2300 2300< Re <10000 Re >10000
Рис. 7.2. Зависимость величины критерия Рейнольдса от режима течения жидкости
Решение уравнения Навье – Стокса для установившегося (стационарного) движения жидкости может быть представлено следующим выражением: f (Eu, Fr, Re) = 0 (7.8) Уравнение (7.8) называют обобщенным (критериальным) уравнением гидродинамики. Равенство численных значений каждой из обобщенных переменных – Eu, Fr, Re – является необходимым и достаточным признаком подобия для широкой группы стационарных
Тепловое подобие
Запишем дифференциальное уравнение конвективного переноса теплоты – уравнение Фурье - Кирхгофа
Для полного описания конвективного переноса теплоты необходимо к уравнению Фурье-Кирхгофа присоединить уравнения Навье–Стокса (7.1) и неразрывности потока и алгебраические уравнения, описывающие зависимости физических свойств жидкости от температуры. Сопоставление локально накопленной теплоты с теплотой, перенесенной с помощью теплопроводности. Сопоставим первые слагаемые в левой и правой части уравнения (7.9)
Проведя преобразования в этом равенстве, перейдем к безразмерному комплексу ar/x2, содержащему две переменные ar/ l 2 =Fo, (7.10) где Fo - критерий (число) Фурье. Сопоставление конвективного (перенос с движущейся средой) и кондуктивного потоков теплоты. Проведем аналогичное сравнение, но второго слагаемого в левой части уравнения Фурье и первого слагаемого в правой части:
После преобразований, аналогичных вышеприведенным, получаем обобщенный комплекс wl/a = Pe, (7.11) где Pe - критерий (число) Пекле. Все вышеприведенные критерии были получены на основе изучения подобия явлений в пределах переноса отдельной субстанции – импульса, вещества, теплоты. Однако, сходство уравнений переноса и сходство физических явлений в механизмах переноса позволяет сопоставлять сходные эффекты для различных субстанций, независимо от их природы. Таким образом, сравнивая потоки импульса и теплоты, получают безразмерный комплекс Рr – критерий (число) Прандтля, характеризующий связь скоростного и температурного полей: Рr = Ранее на основе понятия о пограничном слое было получено выражение α = λ / δт. Это выражение, за очень редким исключением, не является расчетным ввиду неопределенности толщины тепловой пограничной пленки δт. Но проведение соответствующих преобразований, включающих замену δт на определяющий линейный размер l, позволило сформировать безразмерный комплекс:
Физический смысл Nu – это соотношение интенсивностей тепловых потоков по одну сторону поверхности теплообмена, выраженных в форме конвективного ( Проведя аналогичные преобразования для явления массопереноса, получим еще один критерий:
где Sh - критерий (число) Шервуда Sh имеет тот же физический смысл, что и Nu, но не для тепло-, а для массоотдачи. Поэтому в отечественной литературе Sh часто обозначают Nu 2.
|
|||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 564; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.95.167 (0.01 с.) |


 = al.
= al. = а
= а  ,
,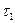 и
и  - время прохождения сходственными частицами путей l1 и l 2; а
- время прохождения сходственными частицами путей l1 и l 2; а  - константа временного подобия.
- константа временного подобия. ;
;  ; или и 1 / и 2 = а и,
; или и 1 / и 2 = а и,
 а
а 
 - теорема Бэкингема: число безразмерных комплексов равно числу всех физически разнородных величин п, существенных для процесса, за вычетом числа первичных величин т.
- теорема Бэкингема: число безразмерных комплексов равно числу всех физически разнородных величин п, существенных для процесса, за вычетом числа первичных величин т. (7.2)
(7.2) , mw = w1 /w2 имеем:
, mw = w1 /w2 имеем: w12/ w22 (7.3)
w12/ w22 (7.3) , (7.4)
, (7.4) р (потеря давления, затраченного на преодоление гидравлического сопротивления) между определенными точками или сечениями. Поэтому обычно применяют несколько иное выражение Еu:
р (потеря давления, затраченного на преодоление гидравлического сопротивления) между определенными точками или сечениями. Поэтому обычно применяют несколько иное выражение Еu: (7.4 a)
(7.4 a) ,
, , (7.5)
, (7.5) и др.
и др. ,
, =
= 
 =
=  = Re = idem, (7.6)
= Re = idem, (7.6)  , можно выразить значение критерия Рейнольдса следующей формулой:
, можно выразить значение критерия Рейнольдса следующей формулой: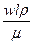 . (7.6 а)
. (7.6 а) =
=  . (7.7 а)
. (7.7 а)
 =
= 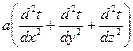 . (7.9)
. (7.9)

 .
. w
w 
 . (7.12)
. (7.12)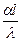 = Nu, (7.13) где Nu - критерий (число) Нуссельта
= Nu, (7.13) где Nu - критерий (число) Нуссельта ) и кондуктивного (
) и кондуктивного (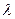 и l) эффектов.
и l) эффектов. = Sh = Nu 2, (7.14)
= Sh = Nu 2, (7.14)


