
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Типичные ошибки в решениях задачи №18Содержание книги
Поиск на нашем сайте
1.Массовая ошибка, наличие которой отметили все эксперты, заключалась в том, что многие участники ЕГЭ, приступившие к решению задачи № 18, из условия вписанности четырёхугольника в окружность и равенства двух его смежных сторон делали ошибочный вывод о том, что этот четырёхугольник квадрат либо ромб. Пример 2.
Рис. 13.2. Комментарии: Уже при оформлении краткой записи задачи в рубрике «дано» автор этого решения указывает ошибочное условие, утверждая, что Пример 3.
Комментарий: ошибочный вывод из условия о том, что Неполнота решения – также один распространенных недостатков решений задачи № 18 (С4). В решениях часто присутствовало либо только попытка доказательства геометрического факта, либо только попытка вычисления площади. При неполном решении, учащимися чаще отдавалось предпочтение задаче на доказательство, нежели задаче на вычисление. Пример 4.
Рис. 13.4. Комментарий: Присутствует только попытка доказательства пункта а), причём всё с той же типичной ошибкой-заблуждением. Оценка, согласно критериям оценивания, 0 баллов.
Задача 19 В ЕГЭ 2015 года задача 19 абсолютно новая. Это задание высокого уровня сложности с экономическим содержанием, проверяющее практические навыки применения математики в повседневной жизни, навыки построения и исследования математических моделей. Задача 19 предполагала: – умение работать с процентами, частями, долями; – владение понятием «математическая модель»; – умение строить математическую модель задачи; – умение применять математические методы для решения содержательных задач из различных областей науки и практики; – умение интерпретировать полученный результат, учитывать реальные ограничения; – владение вычислительными навыками. Приведем один из примеров задачи 19:
«В июле планируется взять кредит в банке на сумму 3 млн. рублей на некоторый срок (целое число лет). Условия его возврата таковы: - каждый январь долг возрастает на 20% по сравнению с концом предыдущего года; - с февраля по июнь каждого года необходимо выплатить часть долга; - в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года. Чему будет равна общая сумма выплат после полного погашения кредита, если наименьший годовой платеж составит 0,24 млн. рублей». . Типичные ошибки в решениях задачи 19 Самой распространенной ошибкой при решении задачи 19 в 2015 году было неверное понимание условия задачи. Большая часть учащихся, приступивших к выполнению задачи 19, трактовала условие «в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года» как «в июле каждого года долг должен быть на одну и ту же сумму меньше», т.е. как «платеж был одинаковым». Изменив условие задачи, учащиеся решали другую задачу, что оценивалось 0 баллов. Пример 1.
Рис.14.1. Комментарии: В решении на рисунке 14.1. выплата по кредиту считается учащимся постоянной – 1,56 млн. рублей, что не соответствует условию задачи. Оценка – 0 баллов. Пример 2.
Рис.14.2. Комментарии: Рассуждения учащегося в решении на рисунке 14.2. далеки от реального условия задачи. Оценка – 0 баллов. Следует отметить, что некоторые работы все-таки отличались оригинальным решением задачи 19. Приведем примеры таких работ. Пример 3.
Комментарии: В решении на рисунке 14.3. логически связанные, обоснованные верные рассуждения. Размышления ведутся «с конца задачи». Решение сопровождается правильными вычислениями. Оценка – 3 балла. Пример 4.
Комментарии: Решение на рисунке 14.4. учащийся оформляет в виде таблицы, предоставляющей всю необходимую информацию. Рассуждения и вычисления верные, но недостаточно обоснованные, поэтому оценка – 2 балла.
Задача 20 В профильном ЕГЭ 2015 года модель задачи №20 (ранее – задача С5) принципиально не изменилась. Уже традиционно это задача с параметром. На этот раз – система уравнений, одно из которых содержит параметр. Это задача высокого уровня сложности.
Задача №20 предполагала: · Наличие обобщенных знаний о различных типах уравнений, их совокупностях и системах; · Владение на высоком уровне понятиями функционально-графической линии курсов алгебры, алгебры и начал анализа и соответствующими умениями; · Владение понятием параметра, модуля действительного числа, уравнения с параметром, системы уравнений; · Умение использовать графическую интерпретацию аналитических данных задачи; · Понимание смысла уравнения с параметром как множества уравнений или множества однотипных линий (с некоторыми исключениями) в прямоугольной системе координат; · Умение выделять случаи при раскрытии модуля и правильно «раскрывать» модуль; · Умение проводить перебор и анализ всевозможных ситуаций, удовлетворяющих вопросу задачи (в данном случае - ситуаций взаимного расположения графиков уравнений системы); · Умение выделять «особые» значения параметра; · Умение использовать частные особенности задачи для рационализации решения и др. Приведём один из примеров задачи №20: «Найдите все значения параметра
Приведем одно из возможных решений задачи 20, предложенное участником ЕГЭ 2015 года. Пример 1.
Рис. 15.1. Комментарий: Участником ЕГЭ предложен графический способ решения. Верный ответ получен обоснованно с помощью верного рассуждения. Согласно критериям оценивания, 4 балла.
|
||||||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 345; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.195.78 (0.006 с.) |



 - вписанный квадрат. Этот факт использован в данном решении как основной. Все остальные ошибки этого решения – следствия необоснованного допущения. Фактически рассматривается задача, отличная от сформулированной в КИМ, или частный случай этой задачи. Согласно критериям, оценка 0 баллов.
- вписанный квадрат. Этот факт использован в данном решении как основной. Все остальные ошибки этого решения – следствия необоснованного допущения. Фактически рассматривается задача, отличная от сформулированной в КИМ, или частный случай этой задачи. Согласно критериям, оценка 0 баллов.
 - ромб. Налицо незнание определения ромба. Кроме того решение содержит противоречащие друг другу записи. Согласно критериям, оценка 0 баллов.
- ромб. Налицо незнание определения ромба. Кроме того решение содержит противоречащие друг другу записи. Согласно критериям, оценка 0 баллов.



 Рис.14.3.
Рис.14.3.
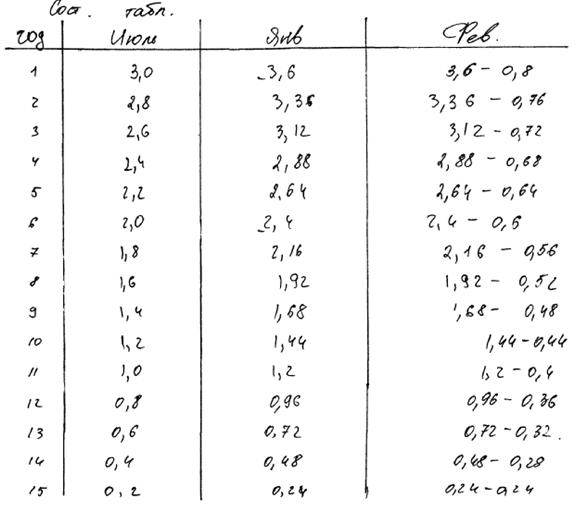
 Рис.14.4.
Рис.14.4. , при каждом из которых система уравнений
, при каждом из которых система уравнений  имеет более двух решений».
имеет более двух решений».




