
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Типичные ошибки в решениях задачи 17Содержание книги
Поиск на нашем сайте
1. Самые распространённые ошибки, сделанных учащимися, приступившими к решению задачи №17 в 2015 году, связаны с формальным перенесением методов и приёмов решения уравнений на неравенства того же типа. Это в частности проявилось в умножение неравенства на выражение с переменной без учёта знака этого выражения и в применении к неравенству свойства пропорции. Следующие примеры иллюстрируют указанные ошибки. Пример 3.
Рис. 12.3 Комментарии: Автором этого решения, представленного на рис. 12.3 применено неравносильное преобразование, а именно: умножение неравенства на выражение с переменной, знак которого зависит от значения этой переменной. Согласно критериям, оценка – 0 баллов. Заметим также, что в последнем переходе, видимо, ученик допустил описку, вместо
Пример 4.
Рис. 12.4 Комментарии: Автор этого решения неправомерно применил для неравенства свойство пропорции («крест-накрест»), что проиллюстрировал соответствующим знаком. Имеется также ошибка вычислительного характера в последнем переходе решения. Оценка, согласно критериям, 0 баллов.
2. Также очень распространённой ошибкой надо считать переход от дробно-рационального неравенства к неравенству, связывающему числители («отбрасывание» знаменателя). В следующем примере представлена именно такая ошибка.
Пример 5.
Рис. 12.5. Комментарии: нарушена равносильность в определённый момент решения. Можно предположить, что ученик использовал в общем случае неверное утверждение о том, что «дробь неотрицательна при неотрицательном числителе». Согласно критериям, 0 баллов. Заметим также, что в этой работе наблюдается ещё одна достаточно распространённая ошибка: аналитическое и графическое представления ответа не соответствуют друг другу, описывая различные числовые множества. Если бы эта ошибка была единственной, то, согласно критериям, решение могло претендовать на 1 балл.
3. Ряд учащихся вместо неравенства решали уравнение. Соответствующий пример ниже. Пример 6.
Рис. 12.6. Комментарии: Учащийся решал задачу, отличную от сформулированной в КИМ. Согласно критериям, 0 баллов. 4. Как уже отмечалось выше, учащиеся, приступившие к решению задачи №17 и получившие ненулевой балл за эту задачу, применяли в основном метод интервалов, предварительно введя вспомогательную переменную. С применением метода интервалов и введением вспомогательной переменной связан ряд достаточно распространённых ошибок. Отдельные из них, согласно критериям, могут расцениваться как вычислительные (ошибка при определении знаков на промежутках, неверное расположение чисел на числовой прямой), другие – принципиальные, связанные с пропуском шагов алгоритма или неверным их выполнением, не могут быть оценены ненулевым баллом. Приведём примеры. Пример 7.
Рис.12.7. Комментарии: Ошибка в определении знака на одном из интервалов вполне может быть признана вычислительной. Учащийся довёл решение до конца, продемонстрировав в целом владение методом замены переменных и методом интервалов. Согласно критериям, 1 балл. Пример 8.
Рис. 12.8. Комментарии: Не сделана обратная замена – необходимый шаг алгоритма. На числовой прямой отмечены значения исходной и введённой переменной. Согласно критериям, 0 баллов. Отдельные учащиеся применили так называемый логический способ решения, осуществив на определённом этапе равносильный переход к совокупности двух систем. Пример правильного решения этим способом представлен на рисунке 12.2. С этим способом решения неравенства связаны следующие ошибки. Это рассмотрение только одного случая положительности (отрицательности) дроби, неверное использование логической символики. Приведём примеры. Пример 9.
Рис. 12.9. Комментарии: В решении рассмотрен только один случай неотрицательности дроби. При решении неравенства (2) автор решения делает ещё одну ошибку логического характера, рассматривает только один случай неотрицательности произведения. Согласно критериям, 0 баллов.
Пример 10.
Рис. 12.10. Комментарии: в представленном выше решении автор многократно неверно использует логическую символику. В явном виде логические операции «конъюнкция» и «дизъюнкция» в школьном курсе математики не изучаются, не изучаются также законы формальной логики. В связи с этим, а также в связи с тем, что имеется верная последовательность всех шагов решения, работа оценена ненулевым баллом, однако, этот балл не максимальный. 5. Необходимым условием решения неравенств повышенной трудности является устойчивые умения тождественных преобразований выражений, в данном случае дробно-рациональных, показательных и логарифмических. Ошибки этого типа, к сожалению, являются распространенными. Приведём пример работы с одной из очень распространённых ошибок такого типа. Пример 11.
Рис. 12.11. Комментарии: автор решения дважды ошибся при выполнении умножения числа на степень. Согласно критериям, 0 баллов. Задача 18 В профильном ЕГЭ 2015 года модель задачи 18 (ранее – задача С4) не претерпела никаких изменений по сравнению с прошлым годом. Это планиметрическая задача, состоящая из двух пунктов: пункт на доказательство геометрического факта и пункт на нахождение одного из компонентов рассматриваемой конфигурации. Задача №18 предполагала: · владение понятиями вписанного многоугольника (треугольника. четырёхугольника), вписанного и центрального углов, подобия треугольников; · знание геометрических фактов, в частности, таких как признаки подобия треугольников; расположение центра окружности, описанной около треугольника; условие вписанного в окружность четырёхугольника; теорема Пифагора и др.; · умение проводить доказательство геометрических утверждений. Приведём пример задачи № 18 и пример одного из возможных решений, предложенного участником ЕГЭ 2015 года: «Диагонали а) Докажите, что б) Найдите площадь треугольника Пример 1.
Рис. 13.1.
|
||||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 599; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.15.92.58 (0.006 с.) |


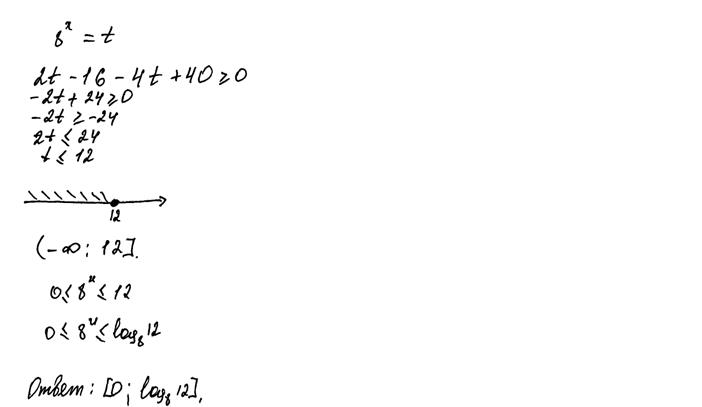
 записав
записав 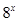 . Учитывая эту погрешность, можно констатировать, что автор этого решения не знает также, что неравенство
. Учитывая эту погрешность, можно констатировать, что автор этого решения не знает также, что неравенство 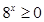 верно при всех значениях переменной. Заметим, что последнее замечание, к сожалению, не редко встречалось и в других работах.
верно при всех значениях переменной. Заметим, что последнее замечание, к сожалению, не редко встречалось и в других работах.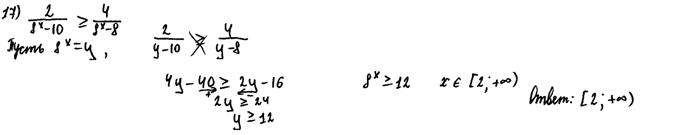
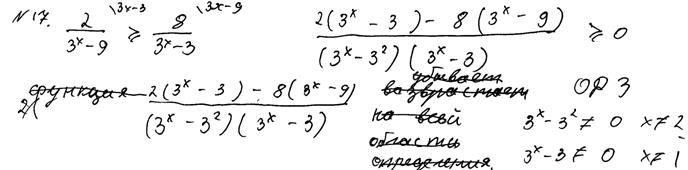
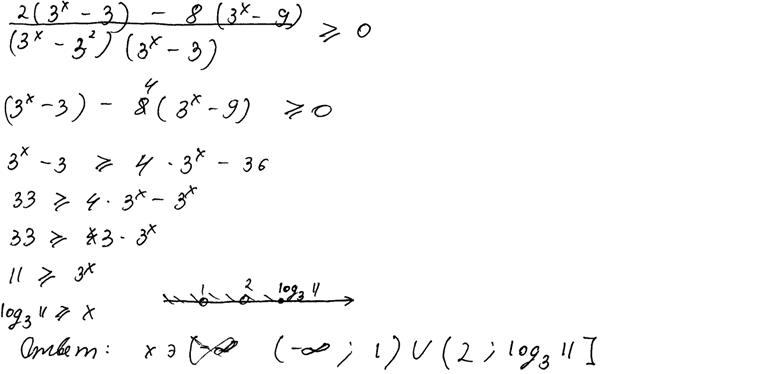
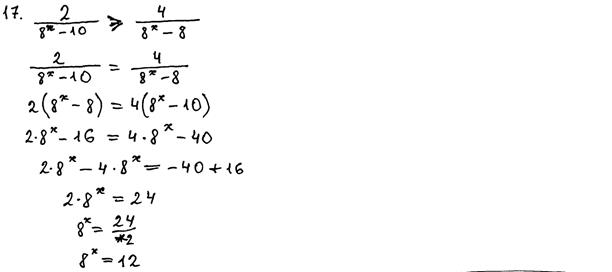

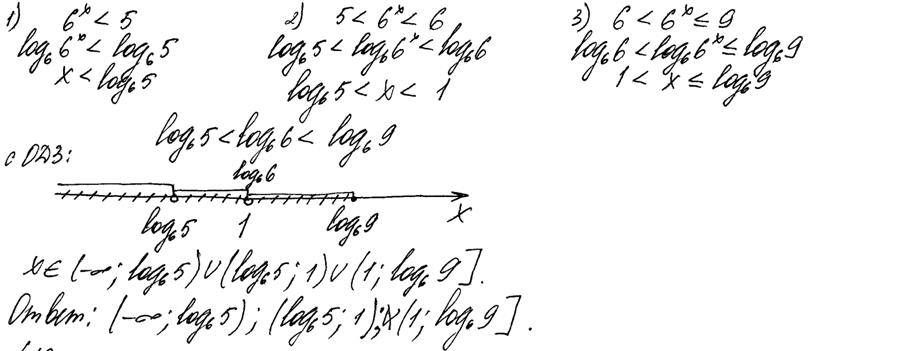
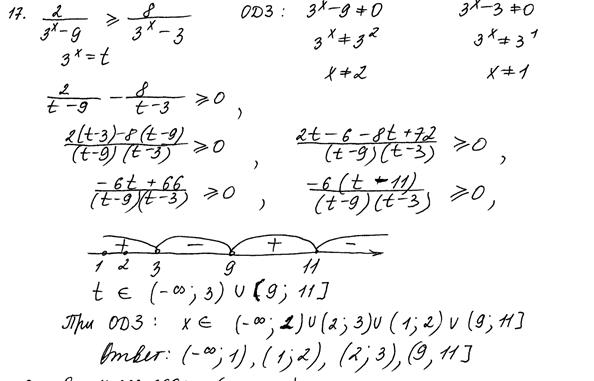
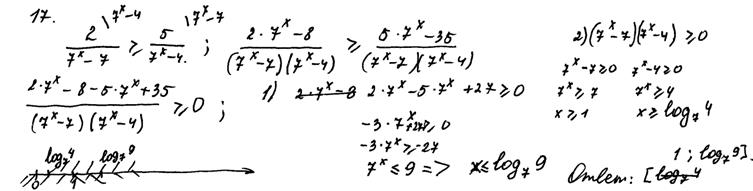

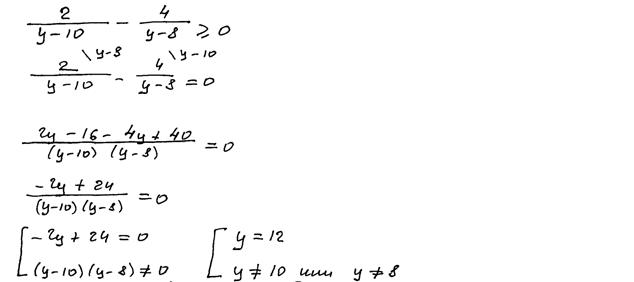
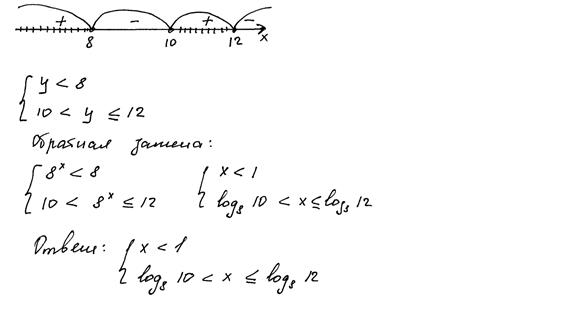

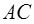 и
и 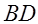 четырёхугольника
четырёхугольника  , вписанного в окружность, пересекаются в точке
, вписанного в окружность, пересекаются в точке  , причём
, причём 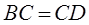 .
.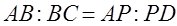 .
.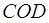 , где
, где  - центр окружности, вписанной в треугольник
- центр окружности, вписанной в треугольник 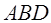 , если дополнительно известно, что
, если дополнительно известно, что  ».
».



