
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Нарушение логики умозаключений, отсутствие логических связок, рассмотрение одного частного случая верного равенства вместо решения задачи.Содержание книги
Поиск на нашем сайте
Пример 7.
Рис. 10.7. Комментарий: Среди работ 2015 года ошибка такого рода приобрела популярность. Учащийся сводит глобальное решение уравнения к исследованию одного частного случая. В данном случае, рассматривая равенство суммы нулю только в том случае, когда каждое слагаемое равно нулю. При чем, эти размышления проводятся без логических связок «и» или «или», но по решению очевидно, учащийся имеет в виду связку «или», что делает рассуждение еще более неправильным. Оценка – 0 баллов. Неточности и описки при решении тригонометрического уравнения или отборе корней уравнения из указанного промежутка Пример 8.
Рис. 10.8. Комментарий: На рисунке 10.8. приведено решение, содержащее изначально ошибку при раскрытии скобок в момент использования основного тригонометрического тождества, что возможно было бы приравнять к описке или вычислительной ошибке. Но, кроме этого, оба простейших тригонометрических уравнения не имеют решения в силу множества значений синуса, на что учащийся не обращает внимания и приводит неверные решения уравнения. Оценка – 0 баллов. 7. Нехарактерная в прошлых годах для задачи такого типа ошибка – неумение работать с иррациональными числовыми выражениями. В связи с этим, для многих учащихся решение квадратного уравнения с иррациональными коэффициентами представляло трудность (чаще всего решение не доводилось до конца). Пример 9.
Рис.10.9. Комментарий: В решении на рисунке 10.9. нет ошибок. Но решение не доведено до конца. Упростив полученные иррациональные выражения, учащийся смог бы сделать вывод о решениях уравнения. Оценка – 0 баллов. 8. По-прежнему, как и в прошлых годах, учащиеся теряют баллы в пункте б) решения задачи 15 по причине отсутствия обоснования отбора корней из промежутка. 1 балл за решение пункта б) выставляется при условии присутствия «следов» отбора корней, что зачастую не имело места в работах участников экзамена 2015 года. Пример 10.
Рис.10.10. Комментарий: В решении на рисунке 10.10. приведено верное, достаточно обоснованное решение пункта а). Но «следы» отбора корней из указанного промежутка отсутствуют (хотя в ответе указаны правильно отобранные корни для пункта б)), что дает эксперту право выставить только 1 балл.
Следует отметить, что по сравнению с 2014 годом при решении задачи 15 улучшилась ситуация с обоснованным отбором корней их промежутка. Учащиеся активно использовали различные способы отбора корней: перебор, решая двойное неравенство, используя единичную окружность или график функции. В основном это было успешно. Задача 16 В 2015 году задача 16 (ранее задача С2) без изменения тематики (Прямые и плоскости в пространстве. Многогранники. Тела и поверхности вращения. Измерение геометрических величин. Координаты и векторы.) стала содержать два пункта с требованиями «доказать» и «найти». Каждый из пунктов независимо оценивался 1 баллом. Задача 16 предполагала: – владение как стереометрическими понятиями (такими как пирамида, высота пирамиды, перпендикулярность прямой и плоскости, угол между прямой и плоскостью и др.) так и планиметрическими (в частности, понятием прямоугольного треугольника, определениями тригонометрических функций острого угла прямоугольного треугольника и др.), а также фактами, связанными с этими понятиями; – умение изображать пирамиду, проводить дополнительные построения, направленные на изображение и поиск угла между прямой и плоскостью; – знание признаков перпендикулярности прямой и плоскости и умение их использовать при решении задачи; – знание обратной теоремы Пифагора и умение ею воспользоваться в нужной ситуации; – владение навыками нахождения угла по значению тригонометрической функции при выполнении вычислительной составляющей решения. Приведем один из примеров задачи 16: В основании четырехугольной пирамиды SABCD лежит прямоугольник ABCD со сторонами AB = 3 и BC = 4. Длины боковых ребер пирамиды а) Докажите, что SA – высота пирамиды. б) Найдите угол между прямой SC и плоскостью ASB.
|
||||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 365; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.58.211.135 (0.006 с.) |

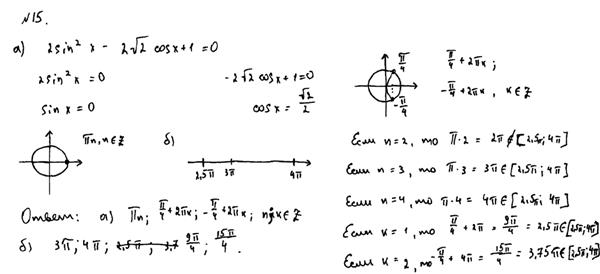
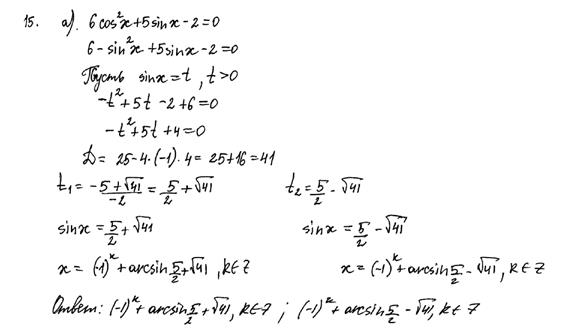
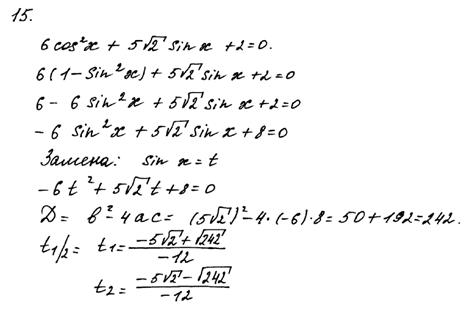
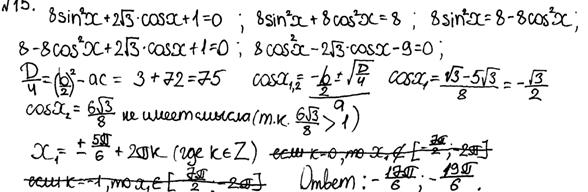
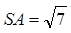 ,
, 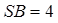 и
и 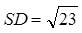 .
.


