
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Типичные ошибки в решениях задачи 20Содержание книги
Поиск на нашем сайте
1.Одна из типичных ошибок - неверное раскрытие модуля. Приведём пример. Пример 2.
Рис.15.2. Комментарий: В решении неверно определены точки смены знака подмодульных выражений. Если считать описанную особенность решения опиской, то раскрываются модули также вопреки определению. Согласно критериям, 0 баллов. Ещё одна достаточно распространённая ошибка состоит в рассмотрении не всех возможных случаев раскрытия модулей. Пример 3.
Комментарий: Задача верно сведена к исследованию взаимного расположения дуг парабол и прямых (аналитически или графически), однако, не рассмотрены ещё два случая раскрытия модуля. Согласно критериям, 1 балл. 3. Задача №20 не является исключением ещё одной распространённой ошибки при оформлении учащимися решения задач с развёрнутым ответом. Это наличие записей, которые в некоторых случаях необходимо расценивать как фактическую ошибку. 4.Достаточно много участников ЕГЭ 2015 года, приступивших к решению задачи 20, подобрали или получили одно значение параметра, при котором система уравнений имеет два или более решений, непосредственной проверкой подтвердили это. В 2014 году, если исходное уравнение было решено для выделенного каким-либо образом значения параметра и показано наличие необходимого количества решений, при отсутствии или ошибочности других рассуждений решение, согласно прошлогодним критериям, оценивалось одним баллом. В 2015 году такой возможности критерии не допускали. Подобные решения в 2015 году оценивались 0 баллов. Приведём пример. Пример 4.
Комментарий: При описании условия случая автором решения использована запись, являющаяся ошибочным утверждением. Согласно общим методическим рекомендациям разработчиков, 0 баллов. Заметим также, что в результате решения получено одно верное значение параметра, однако, даже при отсутствии фактической ошибки в решении, согласно критериям 2015 года, оно не могло бы претендовать на ненулевой балл. Задача 21 В профильном ЕГЭ 2015 года задач 21 (ранее – задача С6) традиционно высокого уровня сложности. На этот раз задача 21 предполагала наличие как обобщенных, так и некоторых частных умений в области математики, а также наличия опыта решения нестандартных задач. Перечислим некоторые из предполагавшихся знаний и умений: - умение строить и исследовать простейшие математические модели; - умение различать логическую структуру утверждений с квантором существования и с квантором общности, знание способов доказательства истинности и ложности утверждений с различными кванторами; знание так называемых кванторных законов и умение переформулировать утверждение с помощью этих законов, сохраняя его смысл; - владение понятием натурального числа; - наличие представления о числовых множествах, отличных от множества натуральных чисел; - знание геометрических фактов, таких как условие существования треугольника, теоремы Пифагора и др.
Приведем один из примеров задачи 21 и вариант её решения, предложенный разработчиками: «Три числа назовём хорошей тройкой, если они могут быть длинами сторон треугольника. Три числа назовём отличной тройкой, если они могут быть длинами сторон прямоугольного треугольник. а) Даны 8 различных натуральных чисел. Может ли оказаться, что среди них не найдётся ни одной хорошей тройки? б) Даны 4 различных натуральных числа. Может ли оказаться, что среди них можно найти три отличных тройки? в) Даны 12 различных чисел (не обязательно натуральных). Какое наибольшее количество отличных троек могло оказаться среди них?». а) Если числа равны 1, 2, 4, 8, 16, 32, 64 и 128, то никакие три из них не образуют хорошую тройку. б) Если одно из чисел является длиной гипотенузы для двух треугольников, то какое-то из оставшихся трёх чисел является длиной катета для этих двух треугольников, а тогда треугольники окажутся равными по гипотенузе и катету. Значит, каждое число может быть длиной гипотенузы не более чем одного треугольника. При этом два самых маленьких числа не могут являться длиной гипотенузы треугольника. Значит, среди четырёх чисел можно найти не более одной отличной тройки. в) Упорядочим числа по возрастанию. Самое большое из них может быть длиной гипотенузы не более чем в четырёх треугольниках (в противном случае одно из оставшихся 11 чисел будет длиной катета в двух треугольниках с данной гипотенузой, а тогда эти треугольники будут равны по гипотенузе и катету). Аналогично, второе по величине число может быть длиной гипотенузы не более чем в пяти треугольниках, третье и четвёртое — в четырёх, пятое и шестое — в трёх, седьмое и восьмое — в двух, девятое и десятое — в одном. Итого, отличных троек может получиться не более 30. Тридцать отличных троек найдётся, например, для следующего набора чисел: 1, Ответ: а) да; б) нет; в) 30.
|
||||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 421; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.44.145 (0.006 с.) |




 Рис. 15.3.
Рис. 15.3.
 ,
, 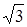 , …,
, …,  .
.


