
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Изучение работы батареи элементовСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Цель работы. Проверить теоретическую зависимость полной, полезной мощности, мощности потерь, падения напряжения во внешней цепи и КПД батареи от силы тока с помощью метода «холостого хода и короткого замыкания».
Описание метода и установки
Электрическая схема измерительной установки (рис.1) состоит из внешнего сопротивлений R источника постоянного напряжения с электродвижущей силой e [1, с.146-147, 149-152; 2, с. 97-99] и внутренним сопротивлением r. В схему включены амперметр и вольтметр, позволяющие измерять ток и падение напряжения во внешней цепи. Из закона Ома для этой замкнутой цепи можно записать выражение [1, с. 151-154; с. 101-103]. e= IR + Ir, (1) где I - сила тока в цепи; U = IR - напряжение на сопротивлении R. Умножив обе части уравнения (1) на силу тока, протекающего по цепи, получим Ie = I2R + I2r. (2) Уравнение (2) представим в виде P = P 1 + P 2 (3) где P = Ie - полная мощность, развиваемая батареей; P 1 = I2R = IU - полезная мощность, т.е. мощность, развиваемая батареей во внешней цепи (на сопротивлении R); P 2 = I2r - потери мощности внутри батареи (на сопротивлении r). Установим зависимость мощностей [1, с.163-165; с. 105-106] от силы тока. Графически (рис.2) зависимость P от I выражается прямой линией, проходящей через начало координат.
откуда, при I m = Так как вторая производная P 1max = Сравнивая по току выражения (6) и получаемое из (1), увидим, что при Потери мощности определяются зависимостью P 2 = I2r (7) Графически зависимость P 2 от I - парабола с вершиной в начале координат, а ее ветвь направлена вверх (рис.2).
Представим выражение для U из (1) в (8)
Из уравнения (9) видно, что зависимость h от I выражается прямой линией, убывающей от значения h = 1 при I = 0 до h = 0 при
I k = Это значение тока - ток «короткого замыкания» [1, с.154]. Действительно, из (1) видно, что при внешнем сопротивлении R = 0 («короткое замыкание» цепи) сила тока достигает наибольшего значения
Полная мощность P = e×Ik и потери мощности P max = P 2max = Найдем значение КПД и соотношения между мощностями P, P 1, P 2 при максимуме мощности P 1 = P 1max. Так как полезная мощность максимальна при условии, что R = r, то
Отсюда, при I = I m, P 1max = 0,5P. Используя (3), получим, при I = I m, P 1max = P 2. Из графиков зависимостей мощностей и КПД от силы тока (рис.2) видим, что условия получения наибольшей полезной мощности P 1max и наибольшего КПД hmax несовместимы. Когда P 1 достигает наибольшего значения, сила тока равна I m и h = 0,5 или 50%. Когда же КПД близок к единице, полезная мощность P 1 мала по сравнению с максимальной мощностью P 1ma x , которую мог бы развить данный источник. Выразив напряжение U = e - Ir, построим зависимость U = f(I) (рис.2). Это - прямая, спадающая от значения U Х (напряжение «холостого хода»), равного U Х = e, до нуля при токе равном току «короткого замыкания». Графический метод определения тока «короткого замыкания» I К и ЭДС e = U Х, так называемый метод «короткого замыкания и холостого хода» является простым и единственным методом, позволяющим, не измеряя, определить I К и e.. На практике он используется следующим образом. Изменяя в некоторых пределах сопротивление R, измеряют ток I и напряжение U. На чертеже строят зависимость U = f(I), графиком которой будет прямая линия. Продолжив ее до пересечения с осью напряжения U, находят значение U Х = e, а до пересечения с осью тока I, находят ток I К. Внутреннее сопротивление источника ЭДС Задание к работе
1. Предварительно подготовьте протокол, в котором начертите таблицу для прямых и косвенных измерений. 2. Постройте на миллиметровой бумаге необходимые оси координат. 3. Соберите электрическую схему установки. В качестве источника с электродвижущей силой e и внутренним сопротивлением r используйте генератор постоянного напряжения ГПН с включенным тумблером «внутреннее сопротивление» R ВН на его передней панели. 4. Изменяя сопротивление R цепи, снимите зависимость U от I и постройте ее график. Определите по графику путем его экстраполяции до пересечения с осями координат значения ЭДС и тока «короткого замыкания» I К.
5. Определите по формуле (10) внутреннее сопротивление r источника тока. 6. Вычислите значения P, P 1, P 2, h. 7. Постройте зависимости этих величин от тока, экстраполируя кривые и прямые до пересечения с осями координат.
Вопросы к защите
1. Закон Ома для замкнутой цепи. Физический смысл ЭДС. 2. Каким должно быть сопротивление вольтметра, чтобы измеренное им значение ЭДС совпало с истинным? 3. Дайте определение полной, полезной мощности и мощности потерь. 4. При каком условии полезная мощность будет максимальна? Докажите. 5. Проанализируйте зависимости мощностей P, P 1, P 2 от силы тока. 6. Коэффициент полезного действия батареи. Проанализируйте зависимость h = f(I). 7. Сравните полученные опытным путем зависимости с теоретическими. 8. Физический смысл напряжения, разности потенциалов.
Список литературы
1. Калашников С.Г. Электричество. - М.: Наука, 1964 2. Савельев И.В. Курс общей физики. - М.: Наука, т. 2, 1978 и последующие издания этого курса.
Лабораторная работа № 14
|
|||||||||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 626; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.98.5 (0.011 с.) |



 , приравняем ее нулю
, приравняем ее нулю
 e - 2Ir, (5)
e - 2Ir, (5) , получим
, получим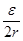 (6)
(6) отрицательна, то при значении силы тока I m мощность P 1 имеет максимальную величину
отрицательна, то при значении силы тока I m мощность P 1 имеет максимальную величину .
. выполняется равенство 2r = R+r или R = r. Следовательно, полезная мощность P 1 максимальна при условии, что сопротивление нагрузки равно внутреннему сопротивлению источника питания R = r.
выполняется равенство 2r = R+r или R = r. Следовательно, полезная мощность P 1 максимальна при условии, что сопротивление нагрузки равно внутреннему сопротивлению источника питания R = r. (8)
(8) (9)
(9) . (10)
. (10) . Полезная мощность P 1 при этом убывает до нуля (рис.2), так как при R = 0
. Полезная мощность P 1 при этом убывает до нуля (рис.2), так как при R = 0 .
. при I = Ik достигают наибольшего значения и равны друг другу
при I = Ik достигают наибольшего значения и равны друг другу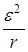 .
. (11)
(11) .
.


